Matemáticas de Selectividad
Ejercicio 3: Reserva 2 de 2023
-
Calcule las derivadas de las siguientes funciones:
𝑓 ( 𝑥 ) = ( − 7 + 𝑥 2 ) 3 𝑒 5 − 𝑥 , 𝑔 ( 𝑥 ) = l n ( 𝑥 4 − 2 𝑥 2 ) 8 − 𝑥 3 . - Represente gráficamente la región acotada comprendida entre la recta
𝑦 = − 2 𝑥 + 6 𝑦 = − 𝑥 2 + 2 𝑥 + 3
Resolución
-
-
Calculamos la derivada de la función
𝑓 . 𝑓 ′ ( 𝑥 ) = 3 ( − 7 + 𝑥 2 ) 2 ⋅ 2 𝑥 ⋅ 𝑒 5 − 𝑥 + ( − 7 + 𝑥 2 ) 3 ⋅ 𝑒 5 − 𝑥 ⋅ ( − 1 ) = 6 𝑥 ( 𝑥 2 − 7 ) 2 𝑒 5 − 𝑥 − ( 𝑥 2 − 7 ) 3 𝑒 5 − 𝑥 = = ( 𝑥 2 − 7 ) 2 ( − 𝑥 2 + 6 𝑥 + 7 ) 𝑒 5 − 𝑥 . -
Calculamos la derivada de la función
𝑔 . 𝑔 ′ ( 𝑥 ) = 1 𝑥 4 − 2 𝑥 2 ⋅ ( 4 𝑥 3 − 4 𝑥 ) ⋅ ( 8 − 𝑥 3 ) − l n ( 𝑥 4 − 2 𝑥 2 ) ⋅ ( − 3 𝑥 2 ) ( 8 − 𝑥 3 ) 2 = ( 4 𝑥 3 − 4 𝑥 ) ( 8 − 𝑥 3 ) 𝑥 4 − 2 𝑥 2 + 3 𝑥 2 l n ( 𝑥 4 − 2 𝑥 2 ) ( 8 − 𝑥 3 ) 2 .
-
Calculamos la derivada de la función
-
Llamamos
𝑓 ( 𝑥 ) = − 2 𝑥 + 6 𝑔 ( 𝑥 ) = − 𝑥 2 + 2 𝑥 + 3 . 𝑓 𝑔 . 𝑓 ( 𝑥 ) = 𝑔 ( 𝑥 ) ⇔ − 2 𝑥 + 6 = − 𝑥 2 + 2 𝑥 + 3 ⇔ 𝑥 2 − 4 𝑥 + 3 = 0 ⇔ { 𝑥 = 1 , 𝑥 = 3 . ( 1 , 4 ) ( 3 , 0 ) . ( 1 , 4 ) .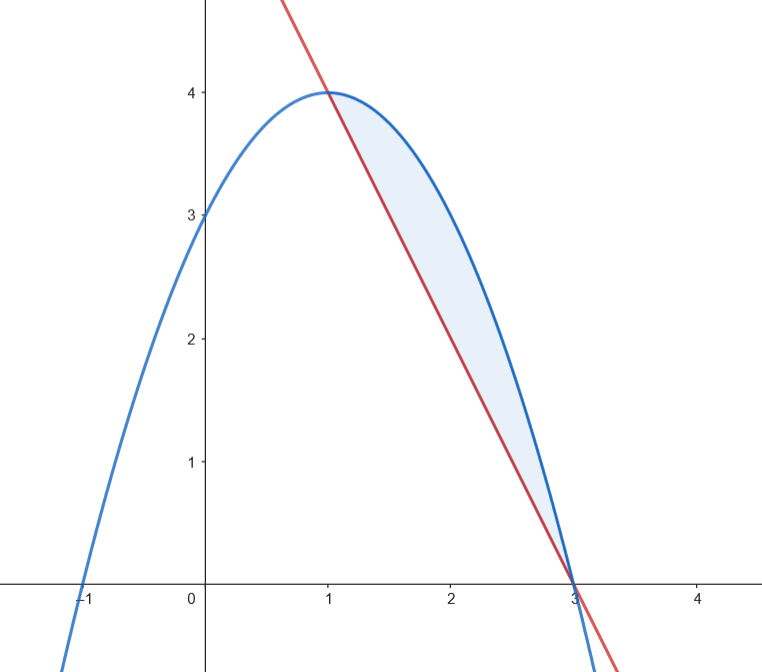 
Calculamos el área del recinto.
∫ 3 1 ( 𝑔 ( 𝑥 ) − 𝑓 ( 𝑥 ) ) 𝑑 𝑥 = ∫ 3 1 ( − 𝑥 2 + 2 𝑥 + 3 − ( − 2 𝑥 + 6 ) ) 𝑑 𝑥 = ∫ 3 1 ( − 𝑥 2 + 4 𝑥 − 3 ) 𝑑 𝑥 = [ − 1 3 𝑥 3 + 2 𝑥 2 − 3 𝑥 ] 3 1 = = − 9 + 1 8 − 9 − ( − 1 3 + 2 − 3 ) = 4 3 𝑢 2 .