Ejercicio 3: Reserva 1 de 2025
-
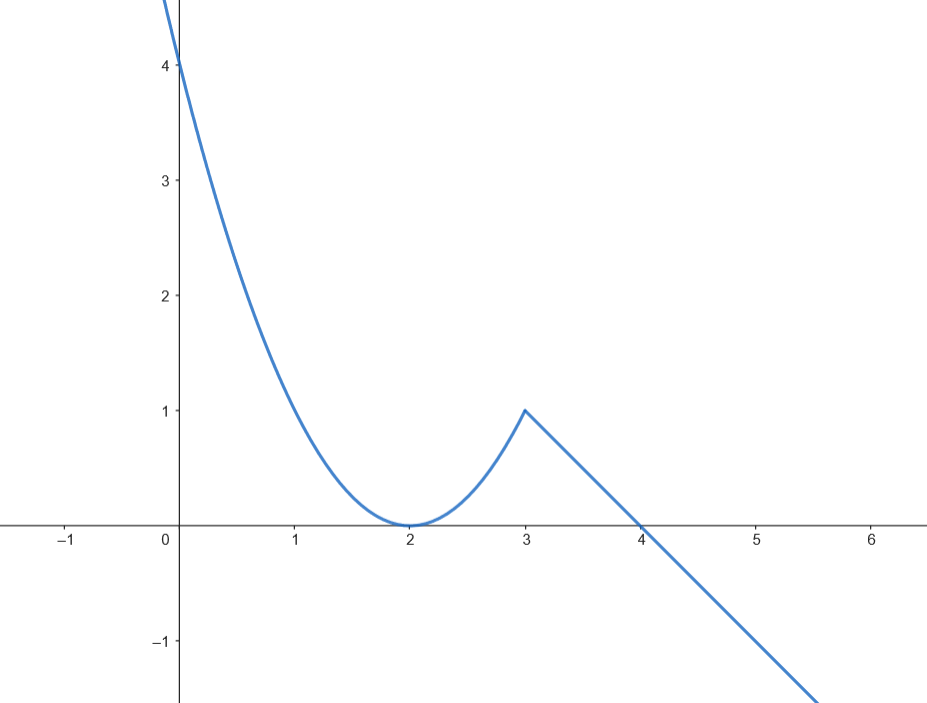
Se considera la función
𝑓 ( 𝑥 ) = ⎧ { { ⎨ { { ⎩ 𝑎 ⋅ 𝑒 𝑥 + 1 , s i 𝑥 ≤ − 1 , 𝑥 2 − 2 , s i − 1 < 𝑥 < 2 , 𝑏 ⋅ l o g ( 1 2 − 𝑥 ) , s i 2 ≤ 𝑥 < 1 2 , 𝑎 𝑏 𝑎 𝑏 𝑓 -
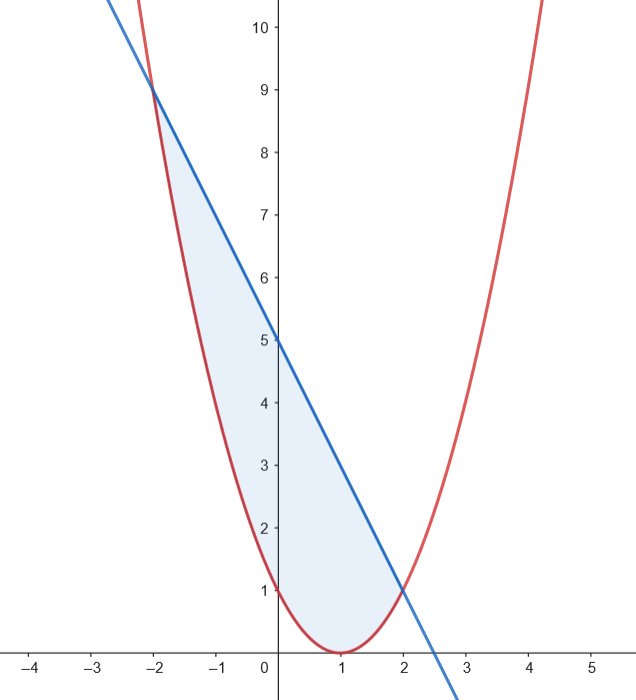
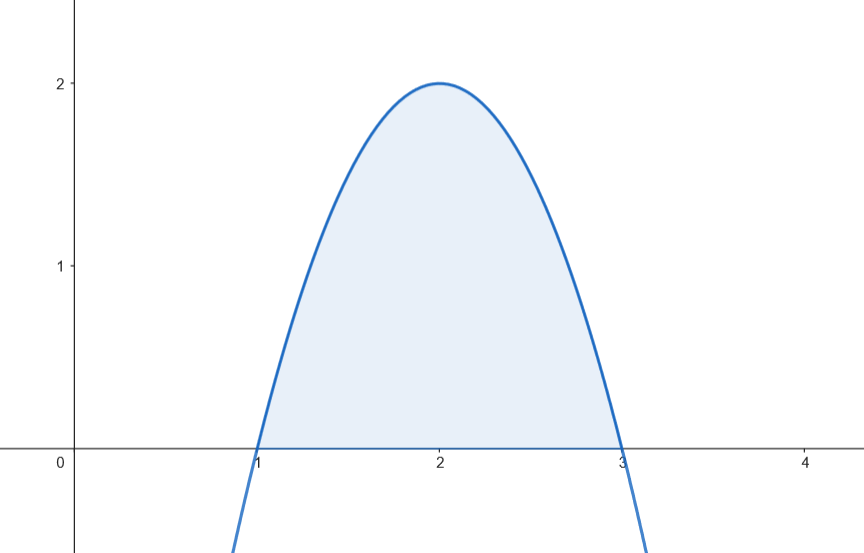
Represente el recinto acotado, limitado por la recta
𝑦 = − 𝑥 + 3 𝑦 = − 𝑥 2 + 5
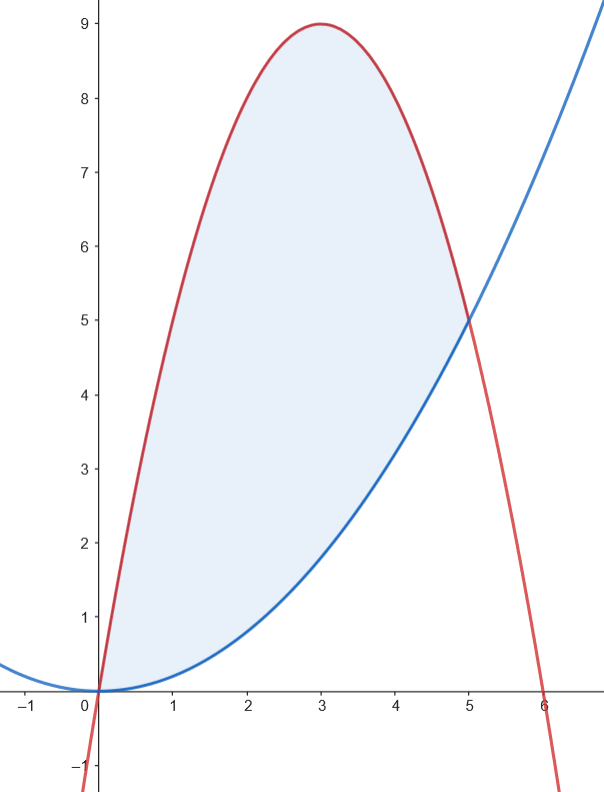
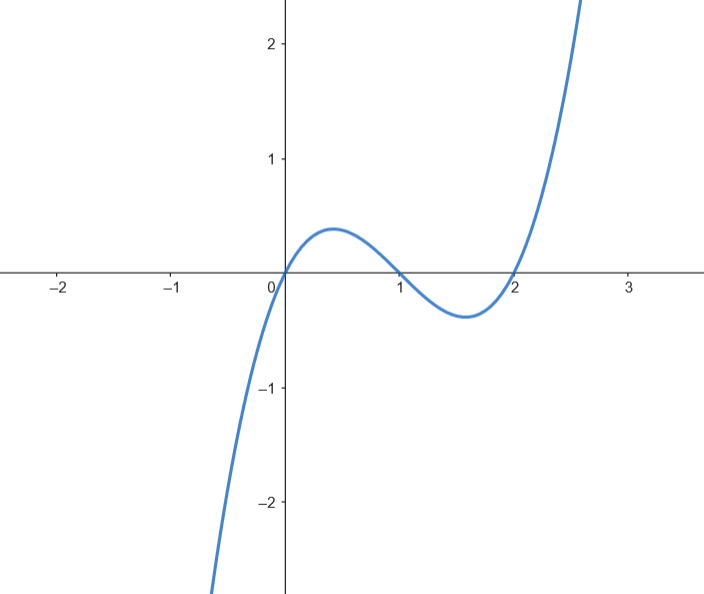
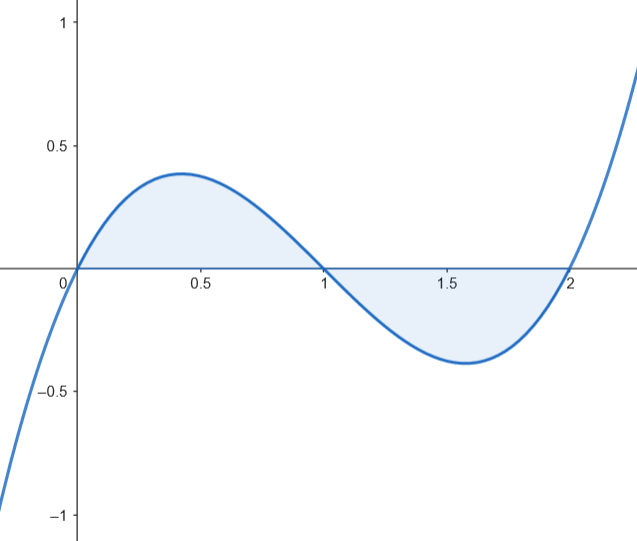
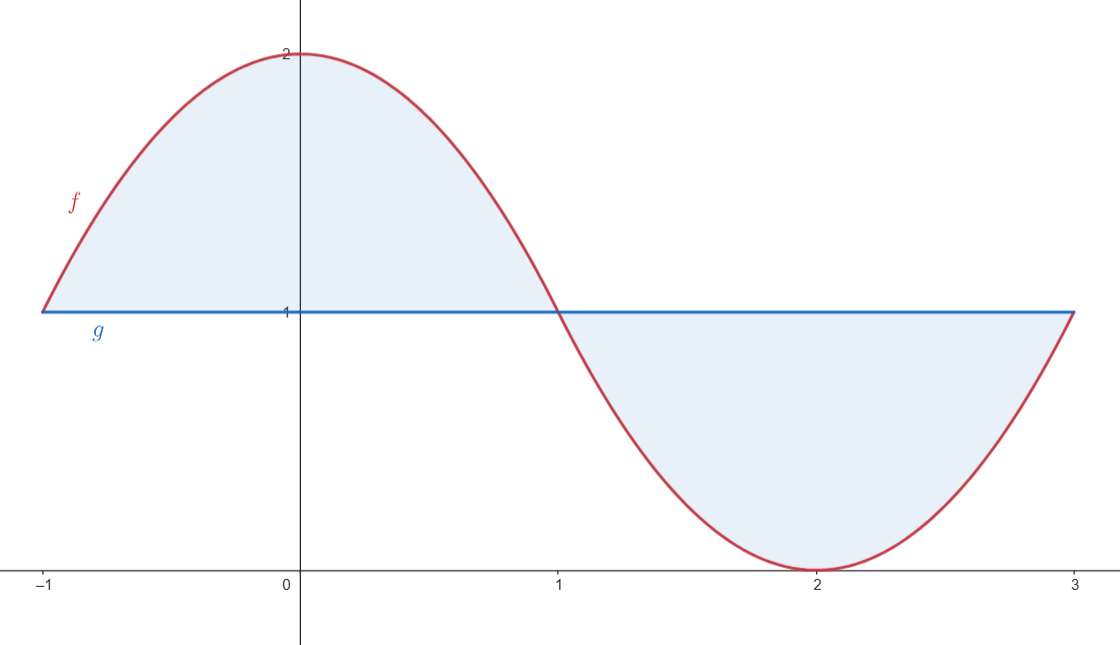 Como los dos recintos tienen la misma superficie, podemos calcular el área como
Como los dos recintos tienen la misma superficie, podemos calcular el área como
 Calculamos el área.
Calculamos el área.
 Calculamos el área.
Calculamos el área.
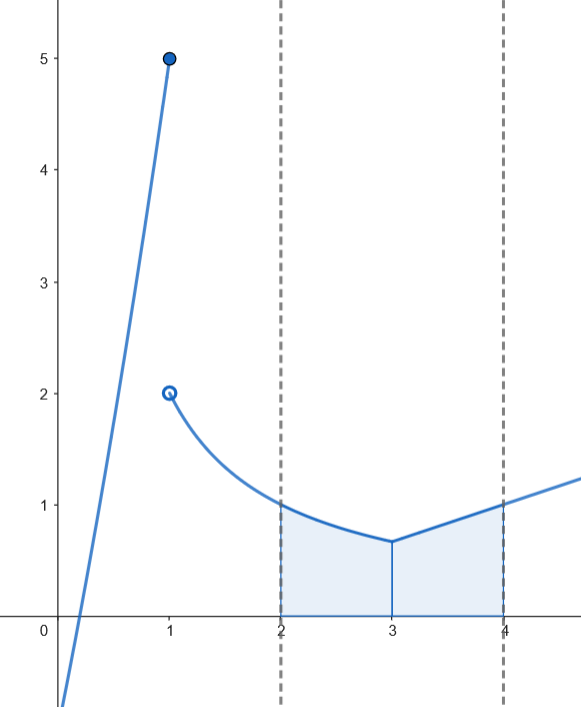 Calculamos el área.
Calculamos el área.
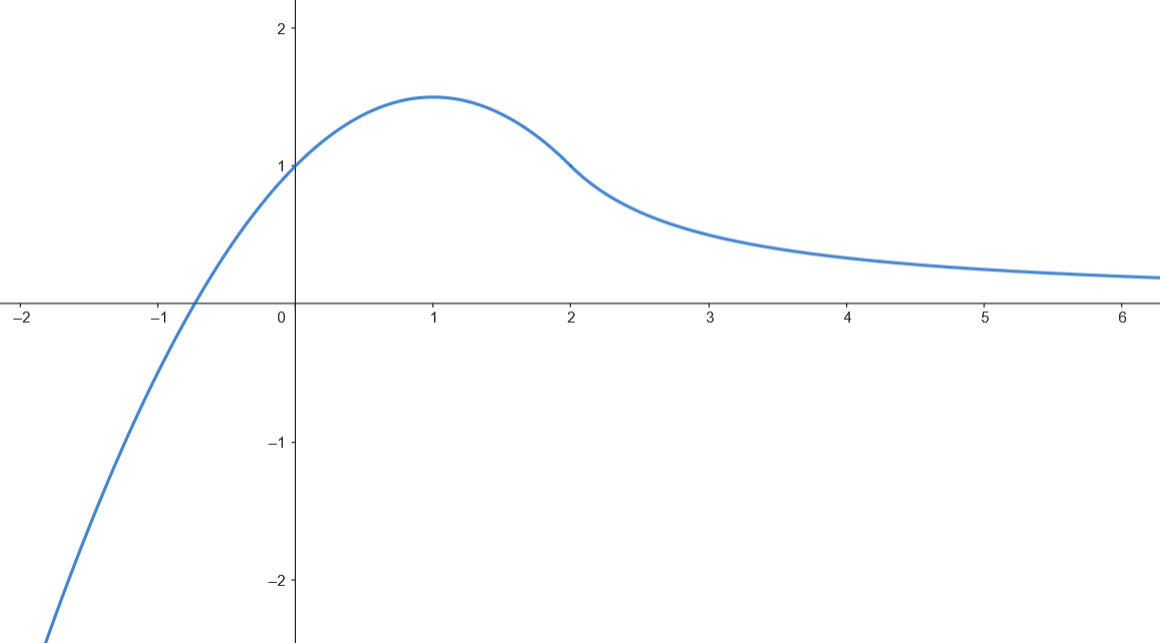
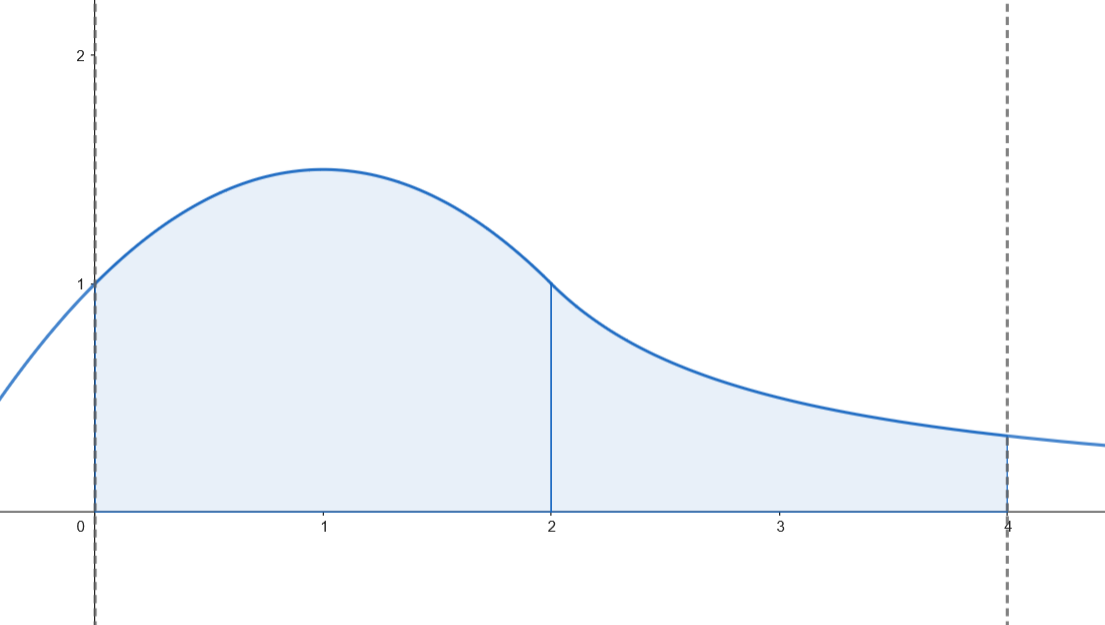 Calculamos el área.
Calculamos el área.
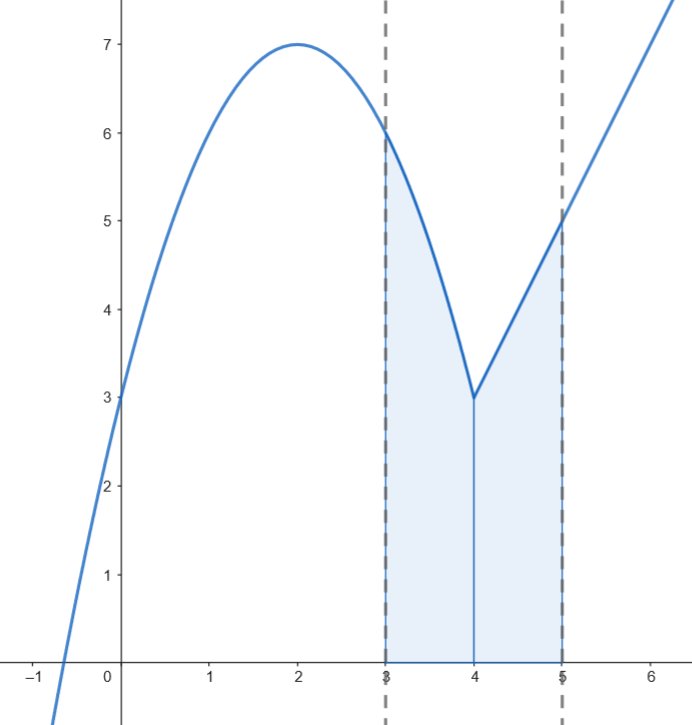 Calculamos el área.
Calculamos el área.
 Calculamos el área.
Calculamos el área.
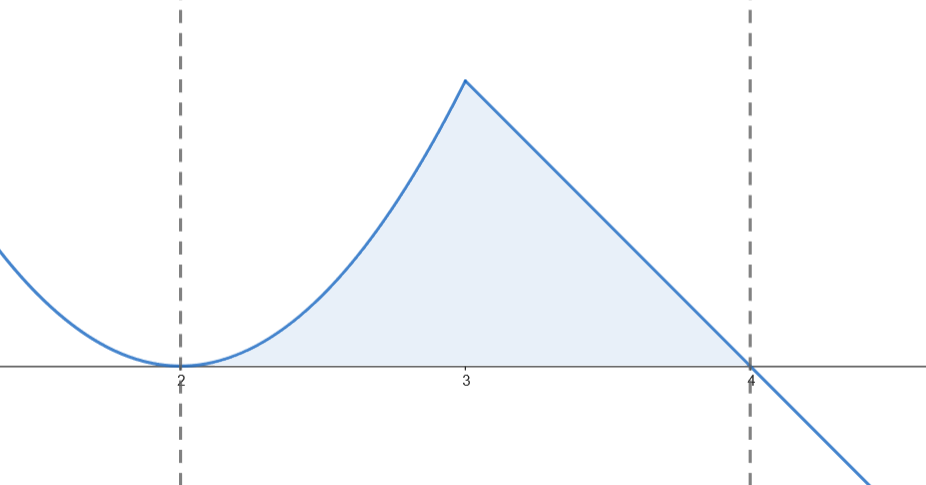
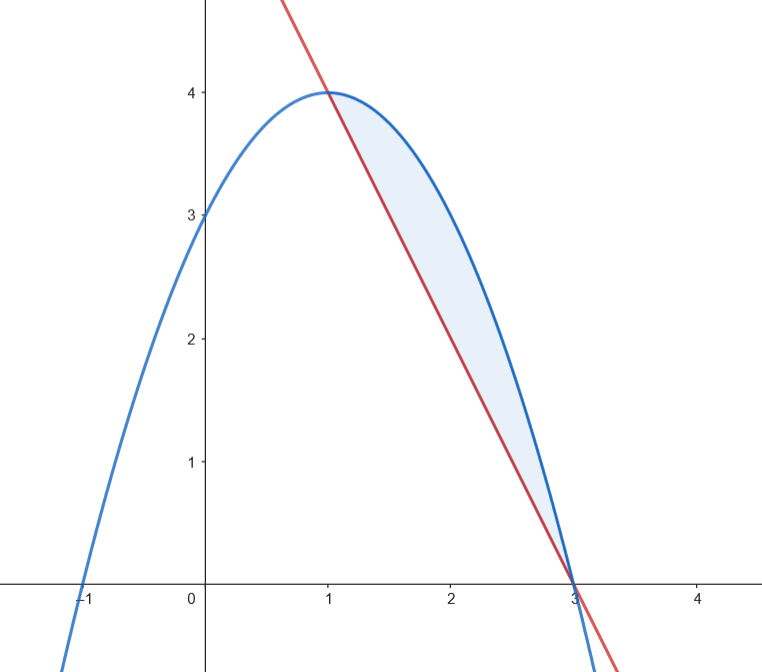 Calculamos el área del recinto.
Calculamos el área del recinto.
 Calculamos el área del recinto.
Calculamos el área del recinto.
 Calculamos el área.
Calculamos el área.
 Calculamos el área.
Calculamos el área.
 Calculamos el área.
Calculamos el área.
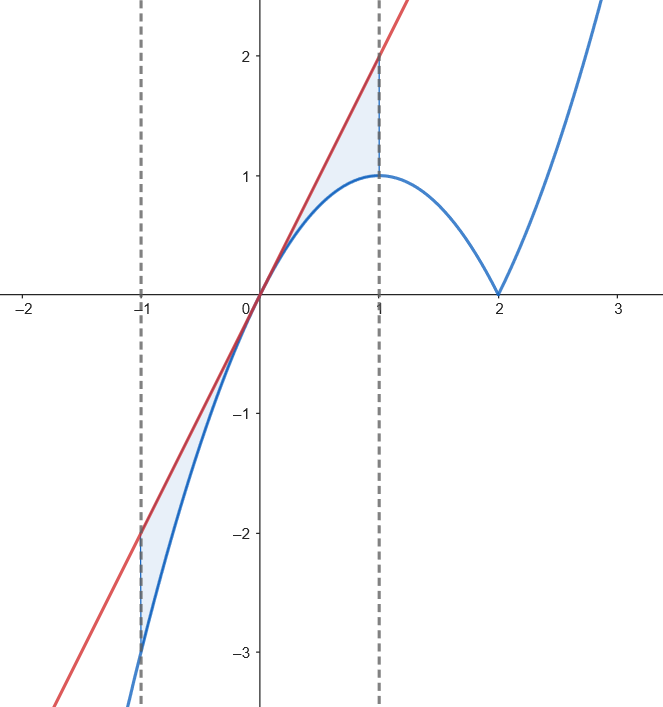
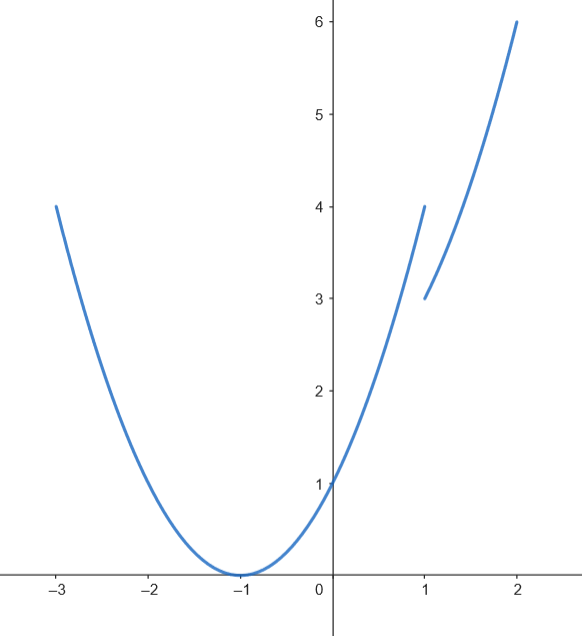 Podemos representar gráficamente el recinto acotado limitado por la gráfica de
Podemos representar gráficamente el recinto acotado limitado por la gráfica de 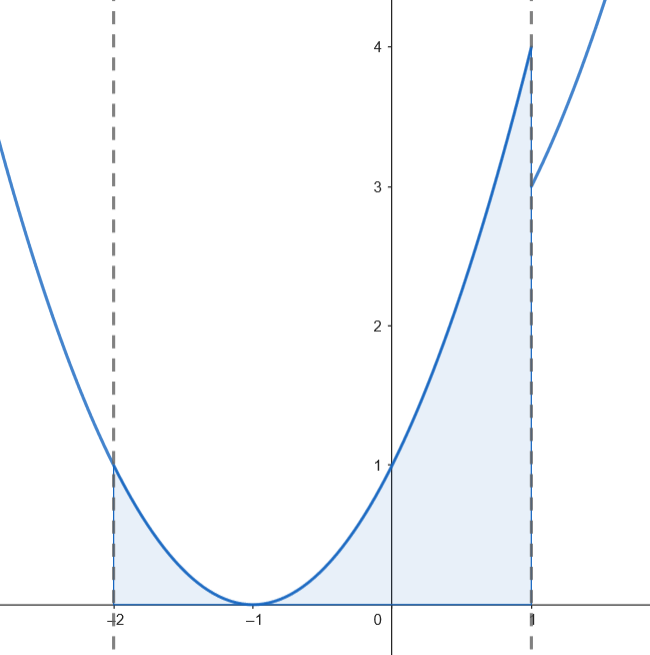 Calculamos el área.
Calculamos el área.
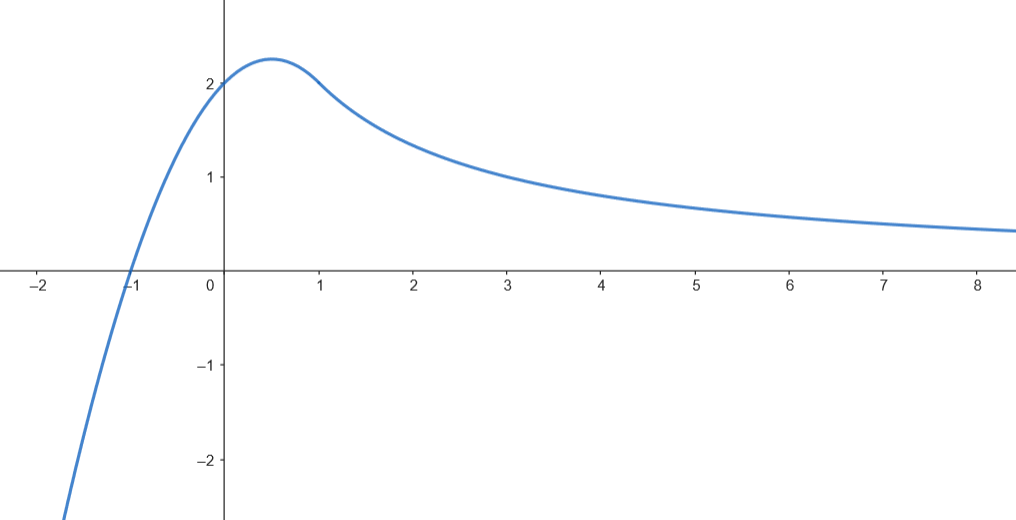
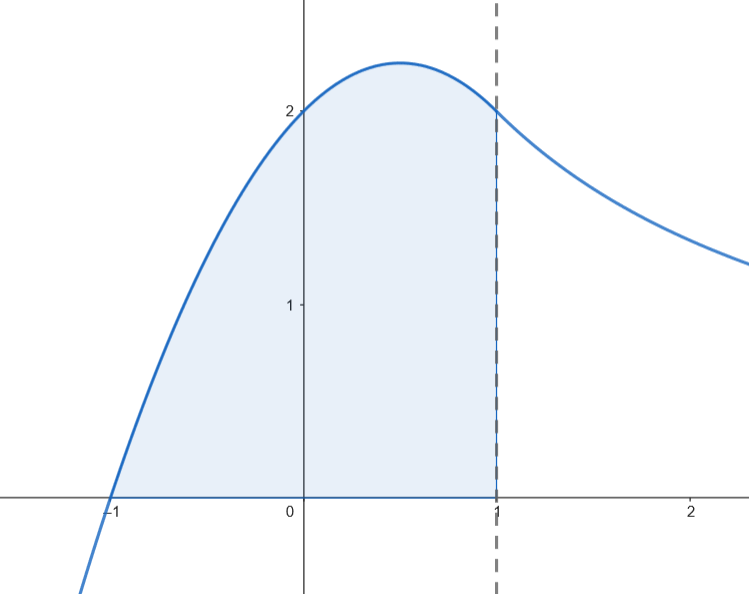 Calculamos el área.
Calculamos el área.
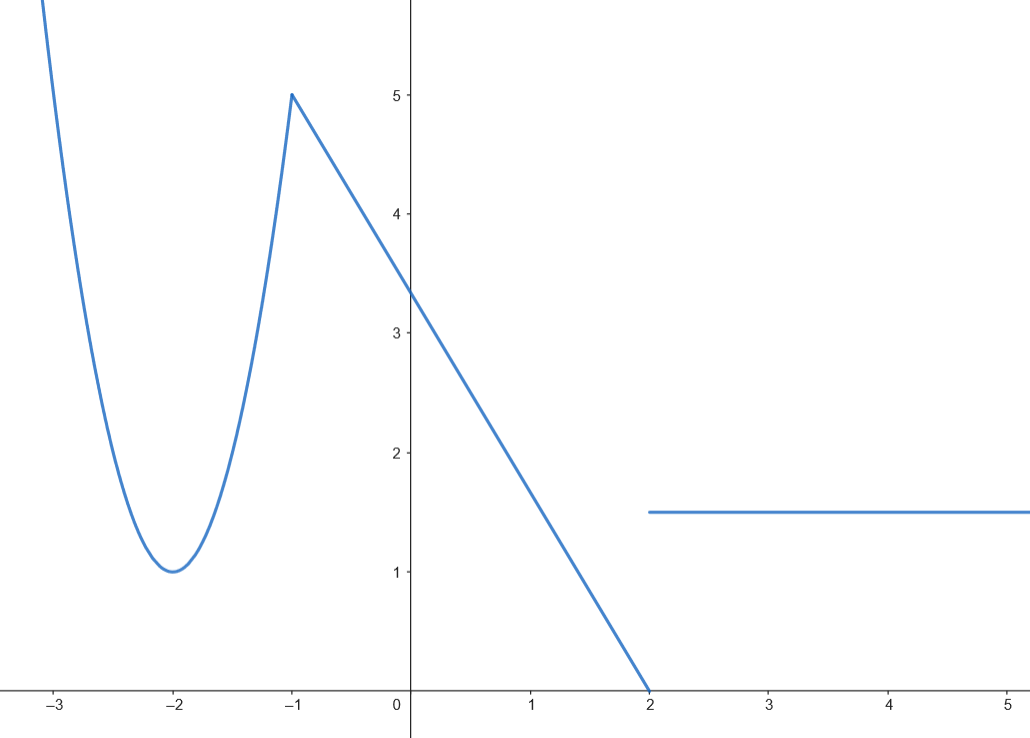
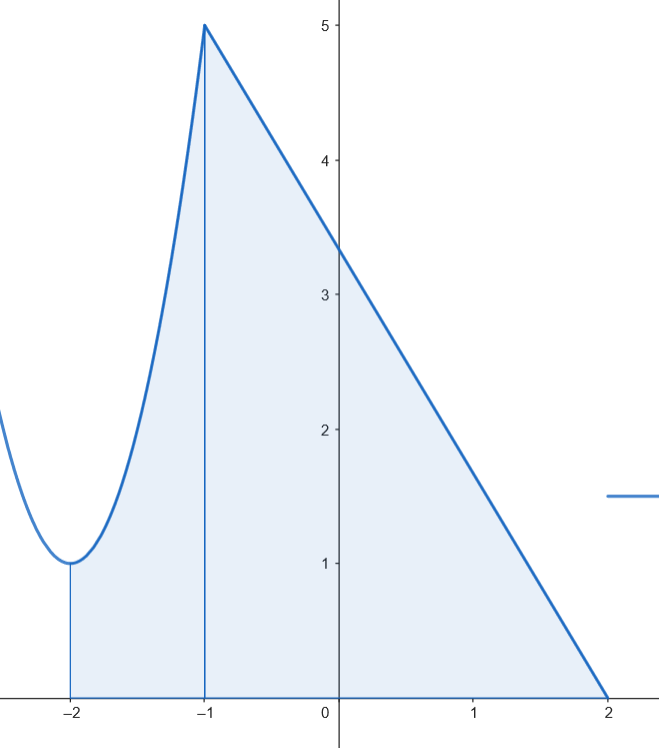 Calculamos el área del recinto.
Calculamos el área del recinto.
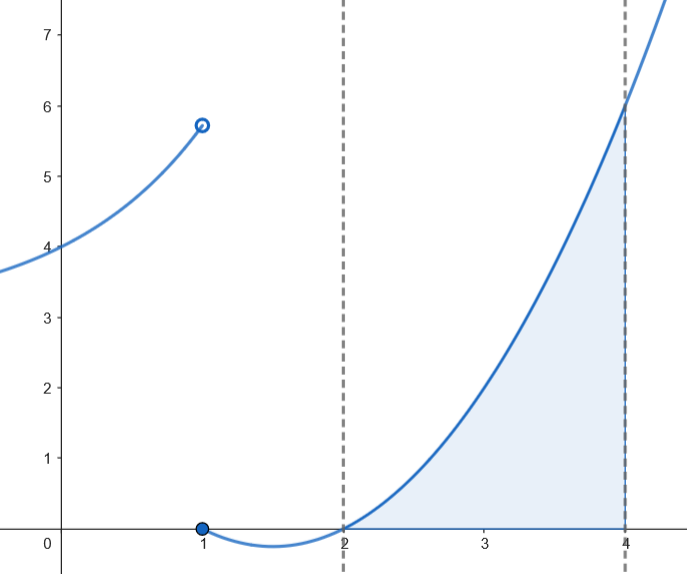
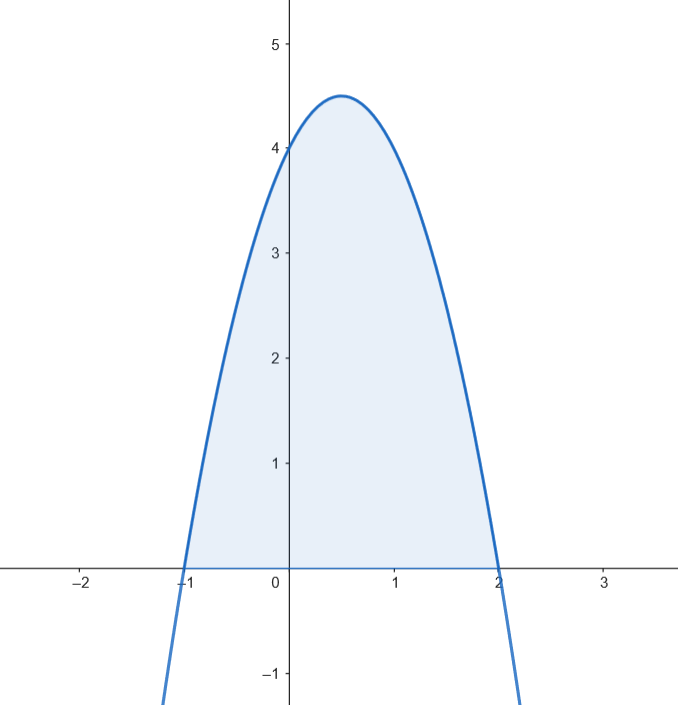
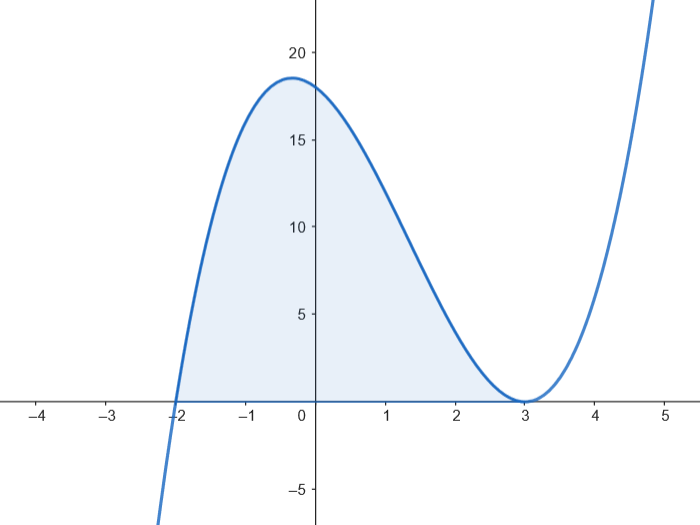
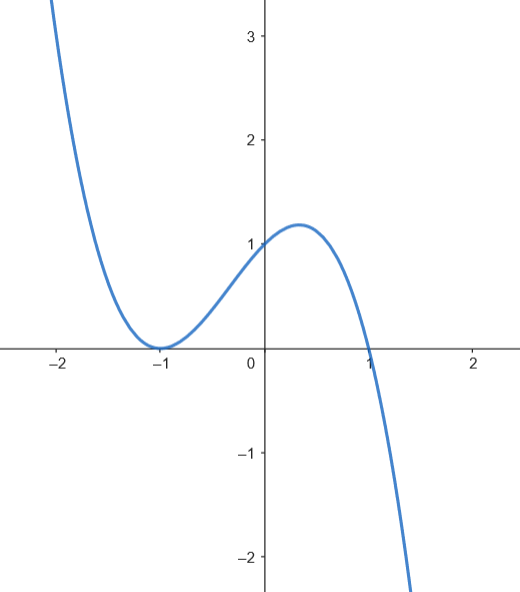 Podemos representar gráficamente el recinto acotado limitado por la gráfica de
Podemos representar gráficamente el recinto acotado limitado por la gráfica de 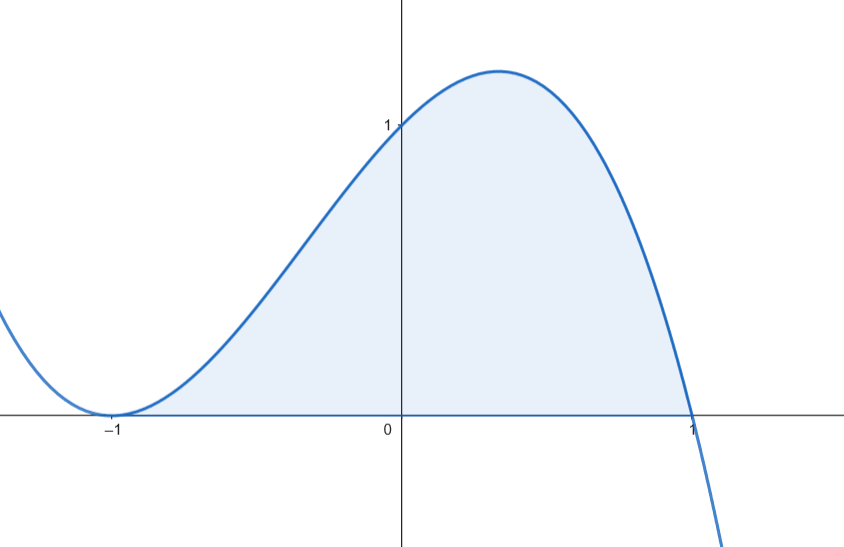 Calculamos el área.
Calculamos el área.
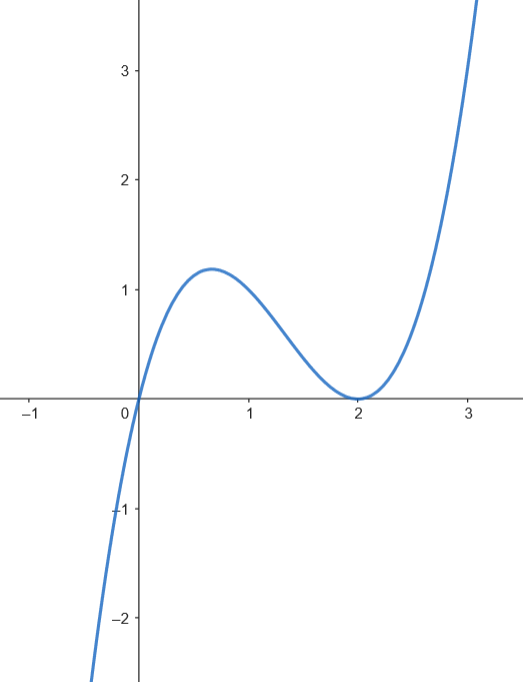
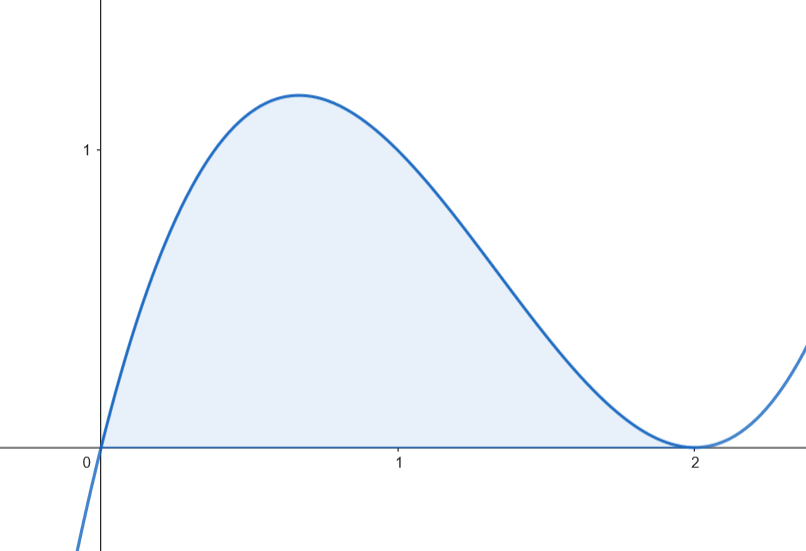 Calculamos el área.
Calculamos el área.
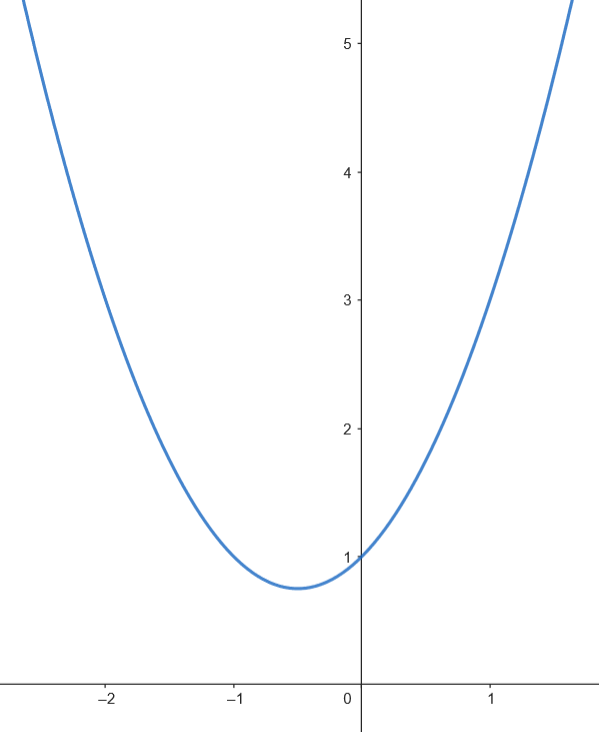
 Calculamos el área.
Calculamos el área.
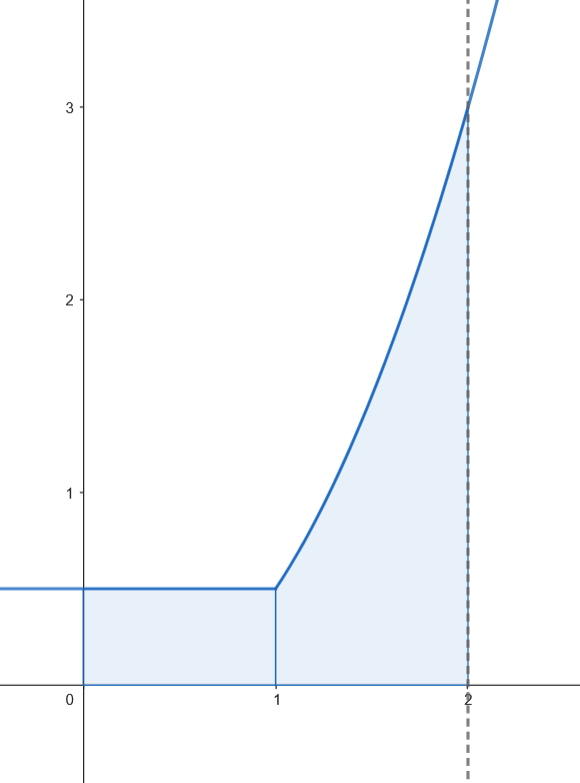 Calculamos el área.
Calculamos el área.
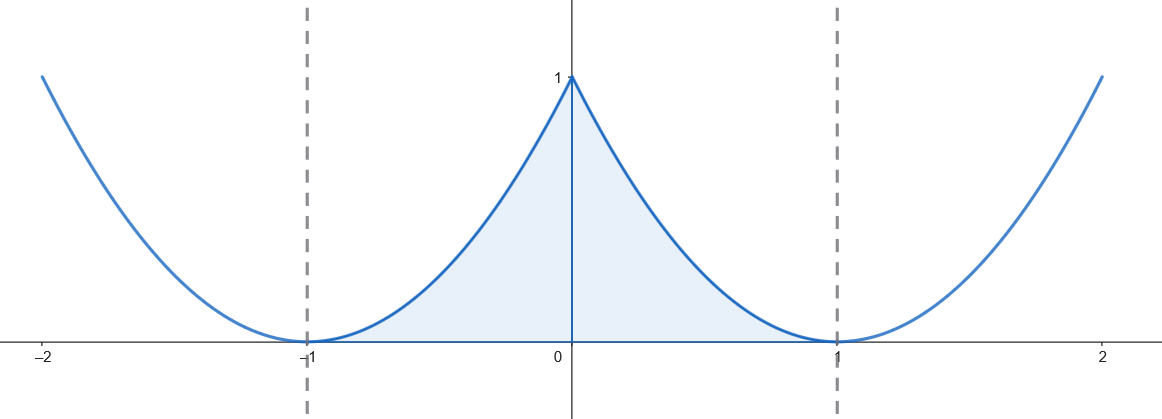 Como el recinto es simétrico, podemos calcular su área como:
Como el recinto es simétrico, podemos calcular su área como:
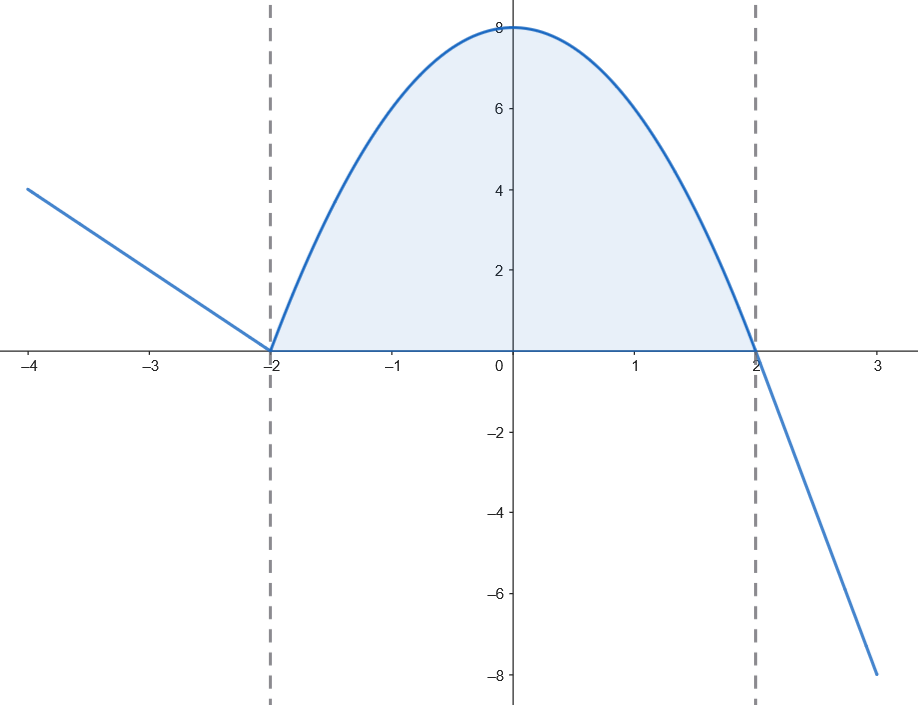 Como el recinto es simétrico, podemos calcular su área como:
Como el recinto es simétrico, podemos calcular su área como: