Ejercicio 1
Se consideran las matrices
-
Determine las matrices
𝑋 𝑌 2 𝑋 − 𝑌 = 4 𝐴 , 𝑋 + 𝑌 = 𝐵 . - Calcule la matriz
𝐶 2 0 2 4 . -
Si
𝐷 2 × 3 𝐴 𝑡 𝐵 + 𝐷 𝐷 𝑡 , 𝐷 𝐵 𝑡 + 𝐴 , 𝐷 𝑡 𝐴 𝑡 + 𝐷 .
Resolución
-
Resolvemos el sistema por sustitución.
Despejando en la segunda ecuación,
𝑋 + 𝑌 = 𝐵 ⇔ 𝑌 = 𝐵 − 𝑋 . 2 𝑋 − ( 𝐵 − 𝑋 ) = 4 𝐴 ⇔ 3 𝑋 = 4 𝐴 + 𝐵 ⇔ 𝑋 = 1 3 ( 4 𝐴 + 𝐵 ) = 1 3 [ ( 0 4 4 0 ) + ( 3 2 2 0 ) ] = 1 3 ( 3 6 6 0 ) = ( 1 2 2 0 ) . 𝑌 = 𝐵 − 𝑋 = ( 3 2 2 0 ) − ( 1 2 2 0 ) = ( 2 0 0 0 ) . -
Calculamos las primeras potencias de
𝐶 . 𝐶 2 = 𝐶 ⋅ 𝐶 = ( 1 0 1 1 ) ( 1 0 1 1 ) = ( 1 0 2 1 ) , 𝐶 3 = 𝐶 2 ⋅ 𝐶 = ( 1 0 2 1 ) ( 1 0 1 1 ) = ( 1 0 3 1 ) , 𝐶 4 = 𝐶 3 ⋅ 𝐶 = ( 1 0 3 1 ) ( 1 0 1 1 ) = ( 1 0 4 1 ) . 𝐶 2 0 2 4 = ( 1 0 2 0 2 4 1 ) . -
-
𝐴 𝑡 𝐵 𝐴 𝑡 𝐵 𝐷 2 × 3 𝐷 𝑡 3 × 2 𝐷 𝐷 𝑡 -
𝐷 2 × 3 𝐵 2 × 2 -
𝐷 𝑡 3 × 2 𝐴 𝑡 2 × 2 𝐷 𝑡 𝐴 𝑡 3 × 2 . 𝐷 2 × 3
-
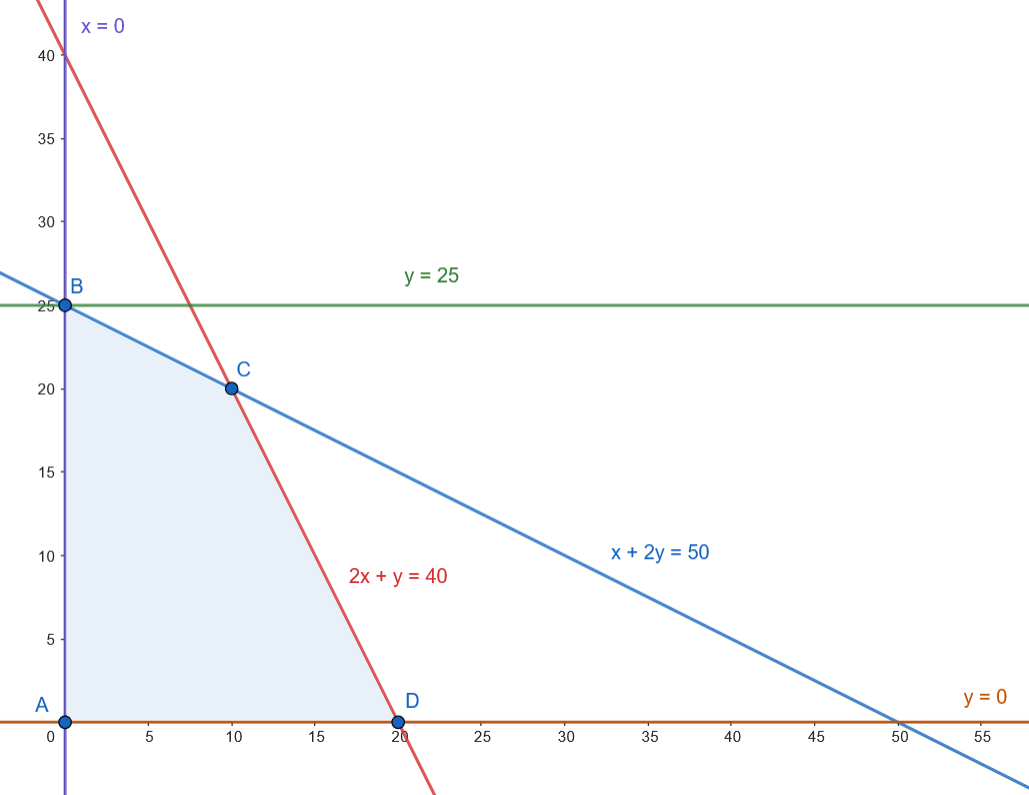 Los vértices son:
Los vértices son:
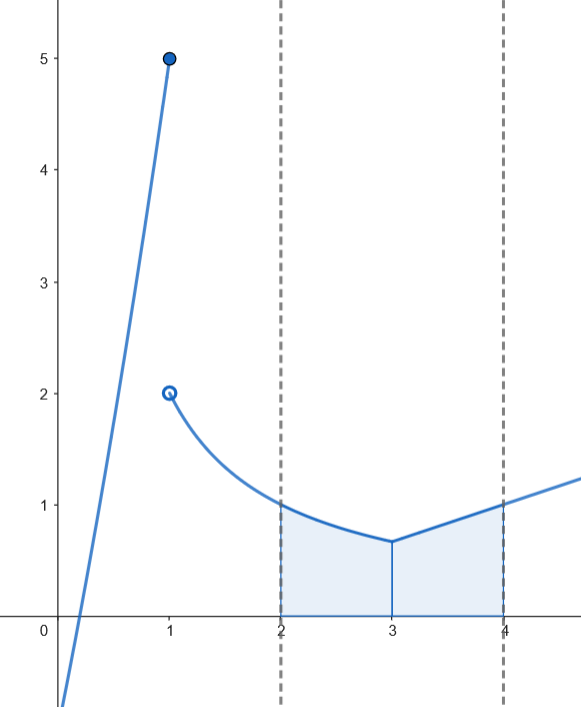 Calculamos el área.
Calculamos el área.
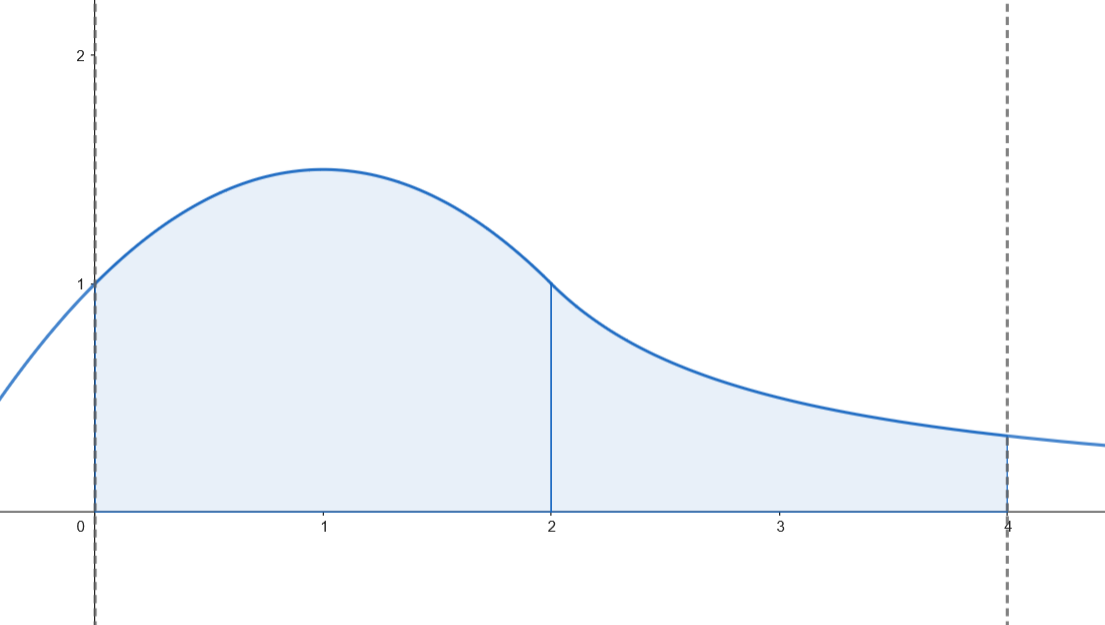 Calculamos el área.
Calculamos el área.