Ejercicio 2: Reserva 1 de 2025
Una empresa de catering dispone semanalmente de 58 horas de cocina, 50 horas de empaquetado y 60 dm3 de almacenamiento en cámaras frigoríficas para elaborar dos tipos de menús: premium y estándar. Ambos menús requieren tiempo, tanto de preparación como de empaquetado, y espacio de almacenamiento en frigoríficos. Concretamente, el menú premium requiere de 2 horas de cocina, 2 horas de empaquetado y ocupa 1 dm3 en frigoríficos. Por su parte, el menú estándar requiere de 3 horas de cocina, 1 hora de empaquetado y ocupa 4 dm3 en frigoríficos. El beneficio obtenido por cada menú premium es de 10,50€ y por cada menú estándar es de 5,50€. La empresa sabe que venderá todos los menús producidos. Determine cuántos menús de cada tipo deben elaborarse semanalmente para maximizar el beneficio total y a cuánto asciende este beneficio.
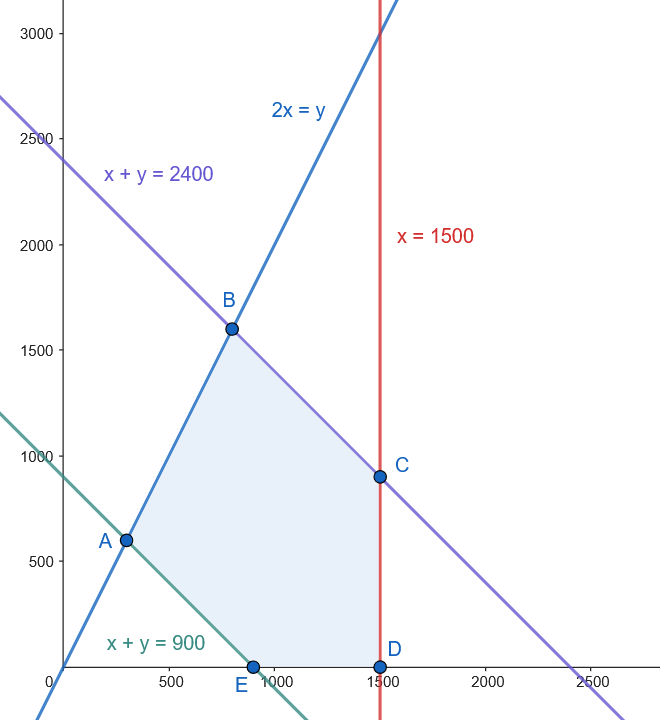 Hallamos los vértices desconocidos.
Hallamos los vértices desconocidos.
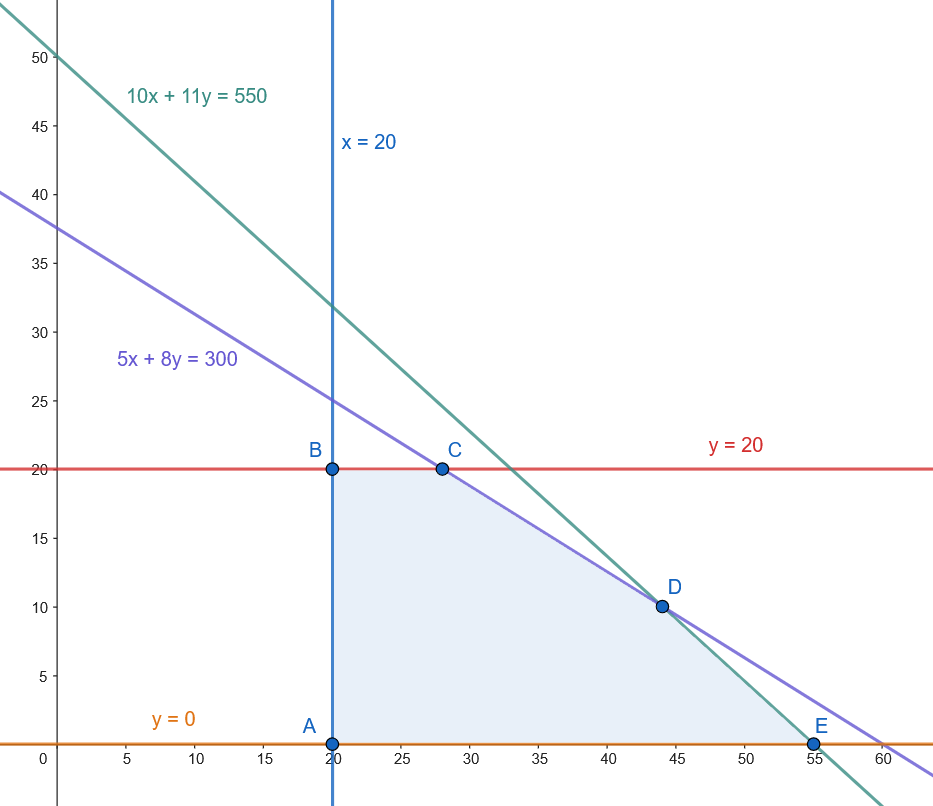 Hallamos los vértices desconocidos.
Hallamos los vértices desconocidos.
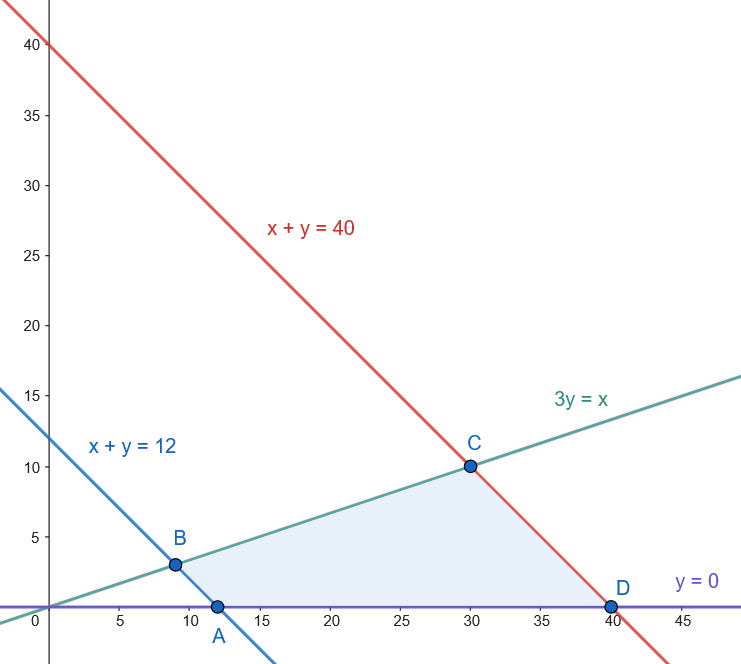 Los vértices son:
Los vértices son:
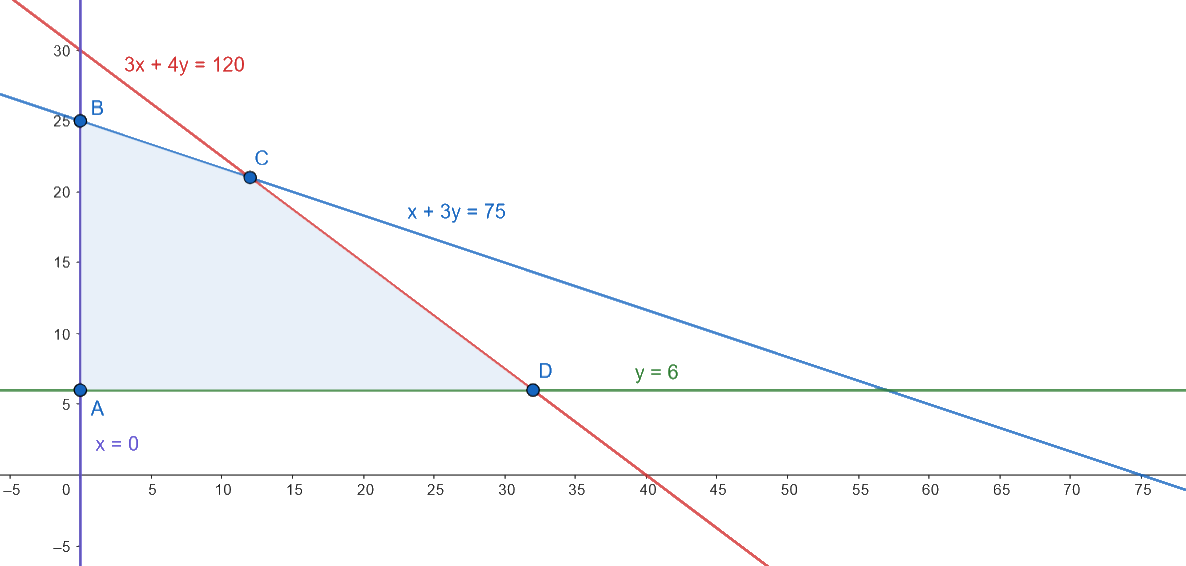 Los vértices son:
Los vértices son:
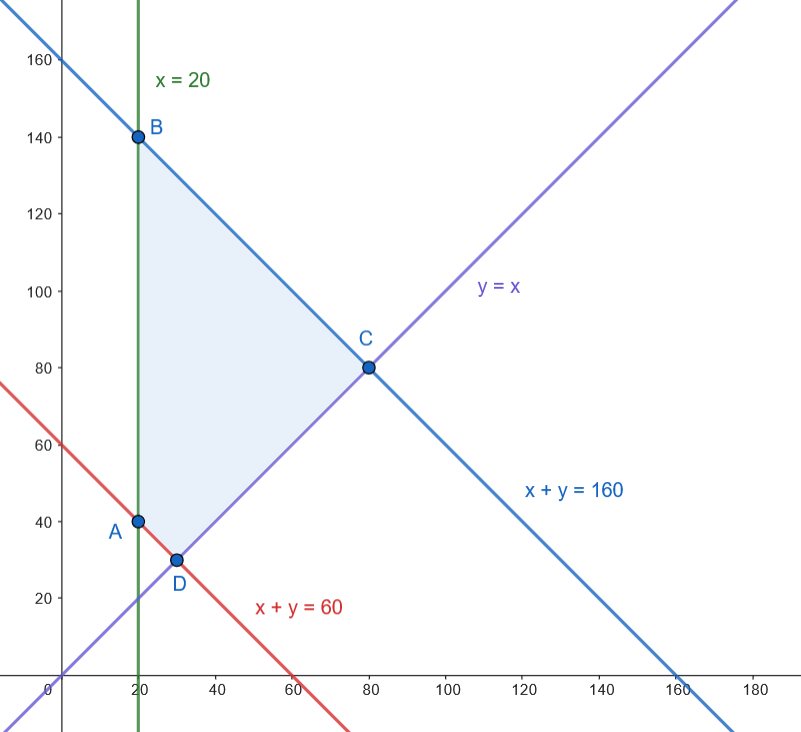 Los vértices son:
Los vértices son:
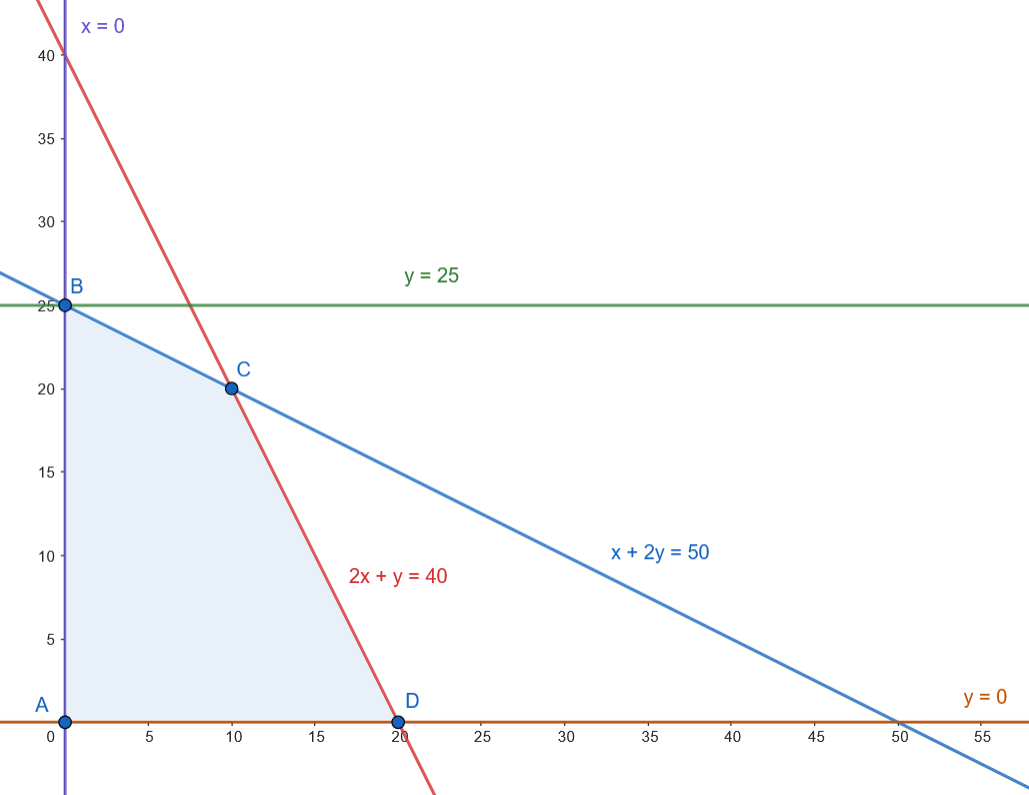 Los vértices son:
Los vértices son:
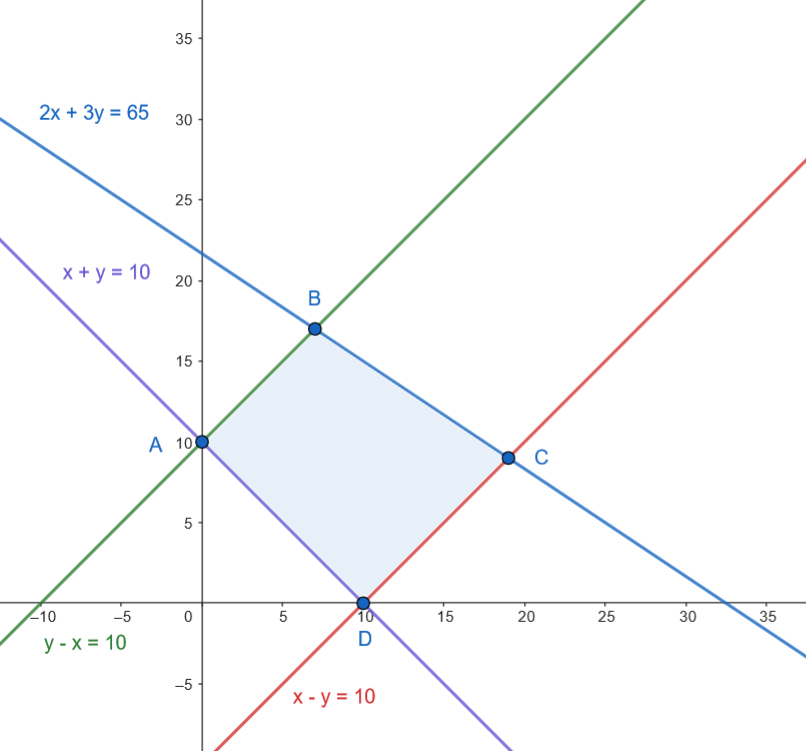 Los vértices son:
Los vértices son:
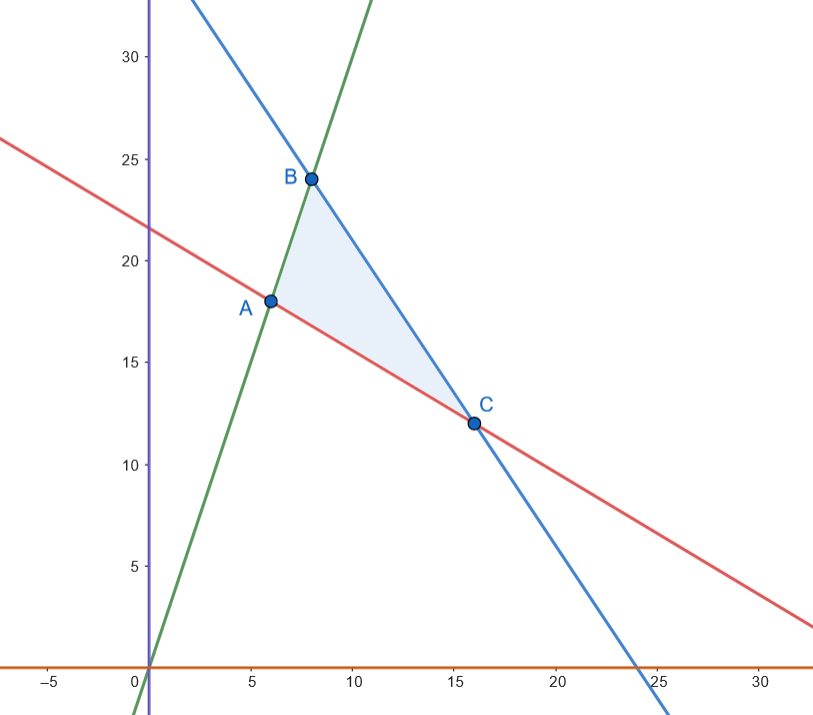 Los vértices son:
Los vértices son:
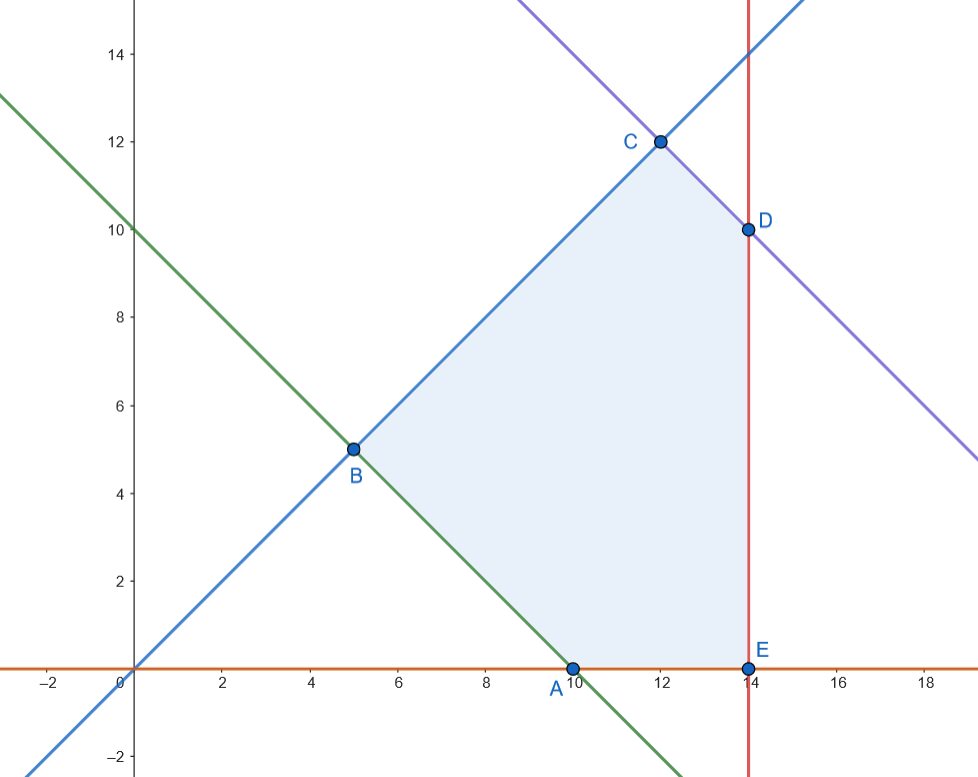 Los vértices son:
Los vértices son:
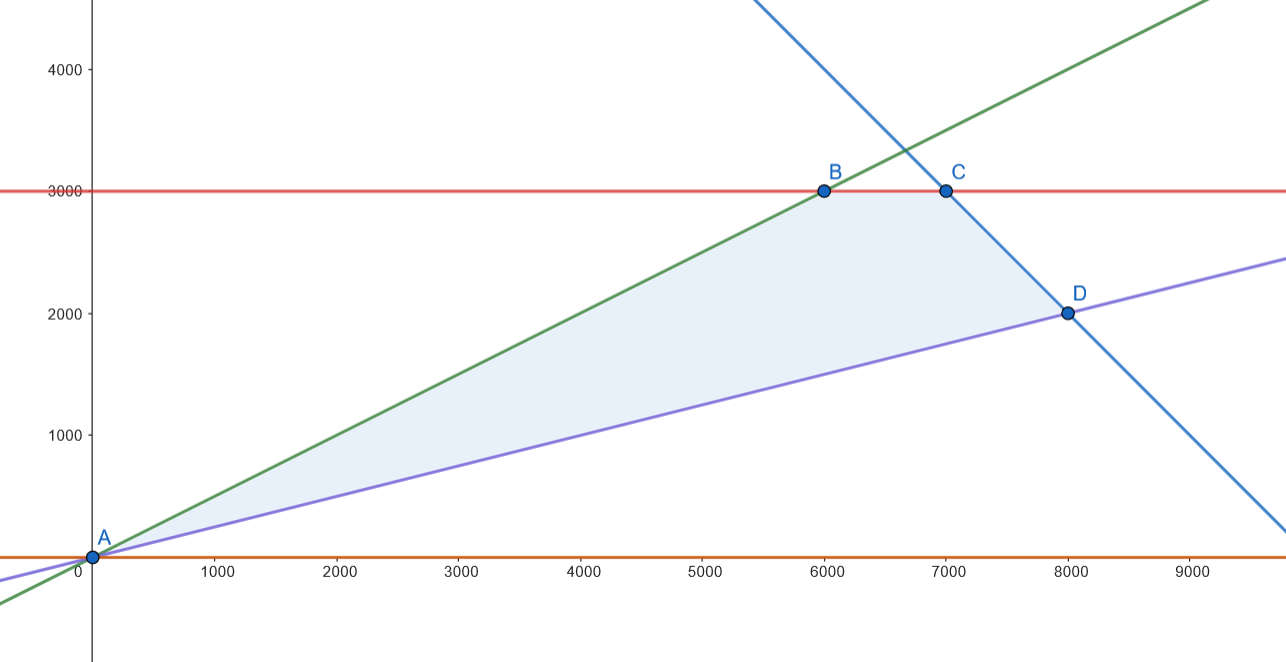 Los vértices son:
Los vértices son:
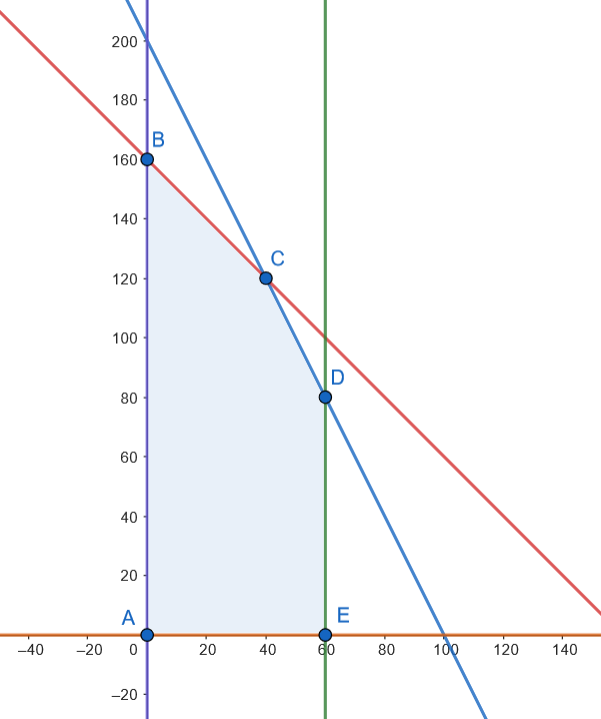 Los vértices son:
Los vértices son:
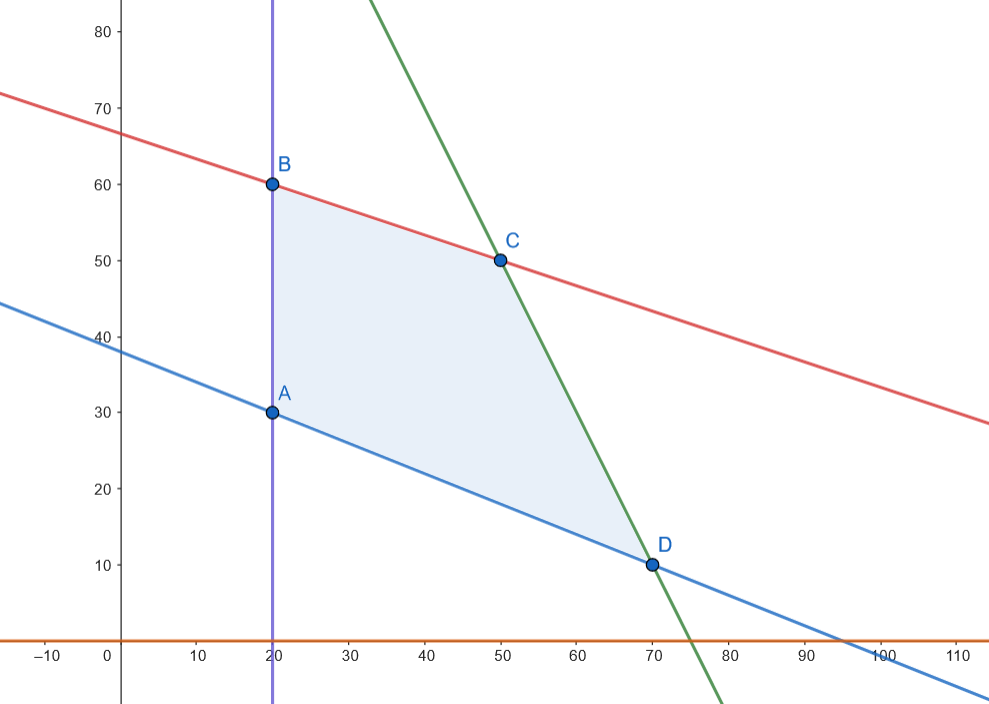 Los vértices son:
Los vértices son:
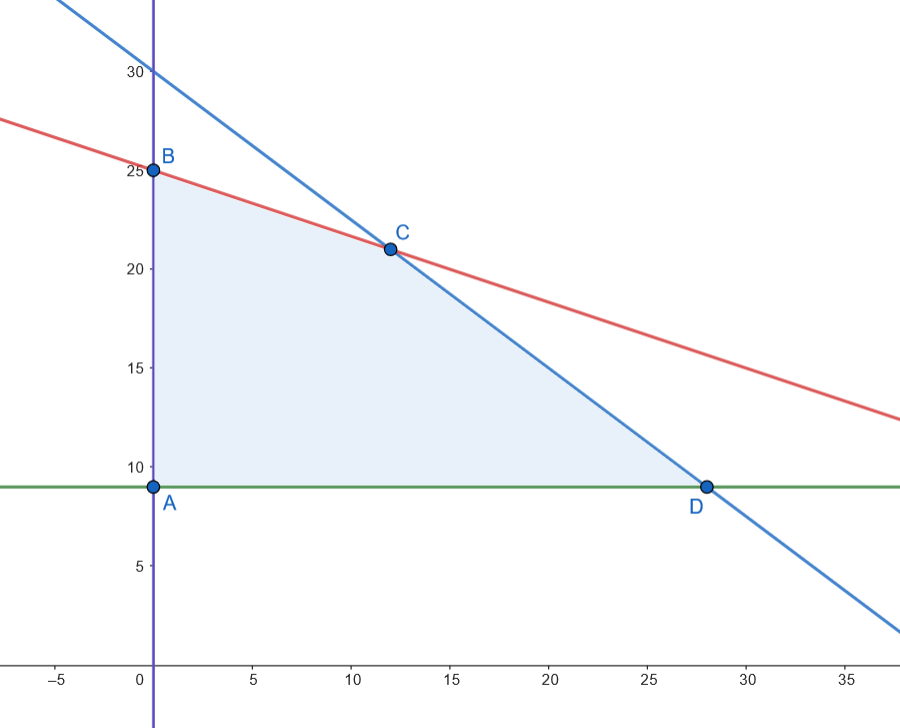 Los vértices son:
Los vértices son:
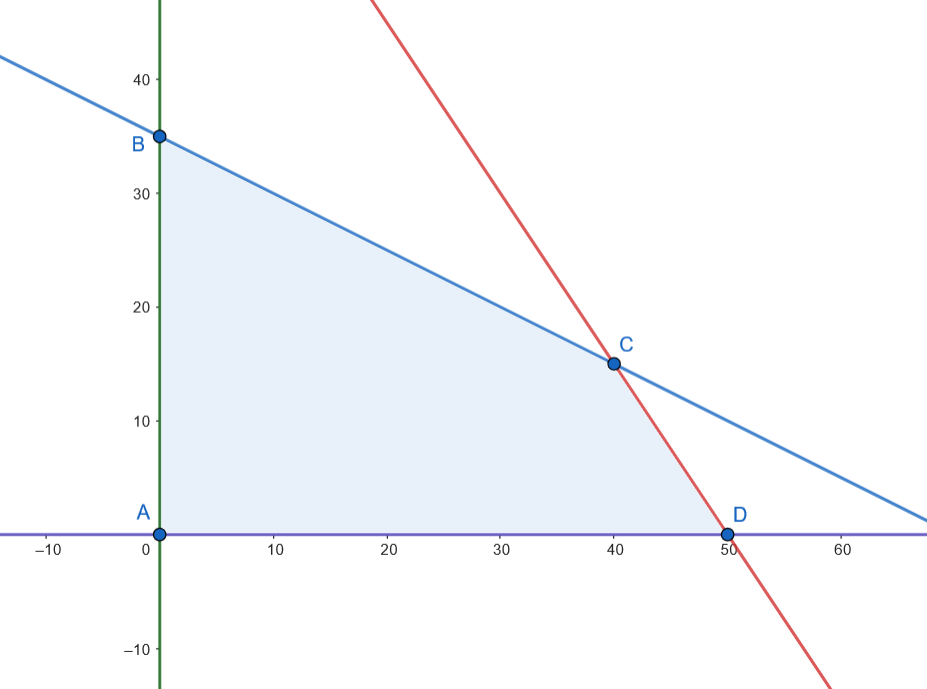 Los vértices son:
Los vértices son:
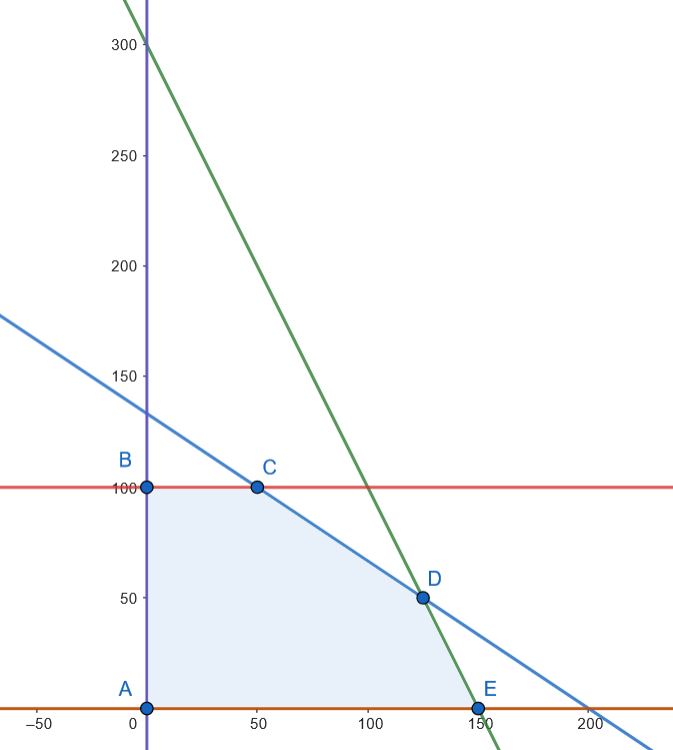 Los vértices son:
Los vértices son:
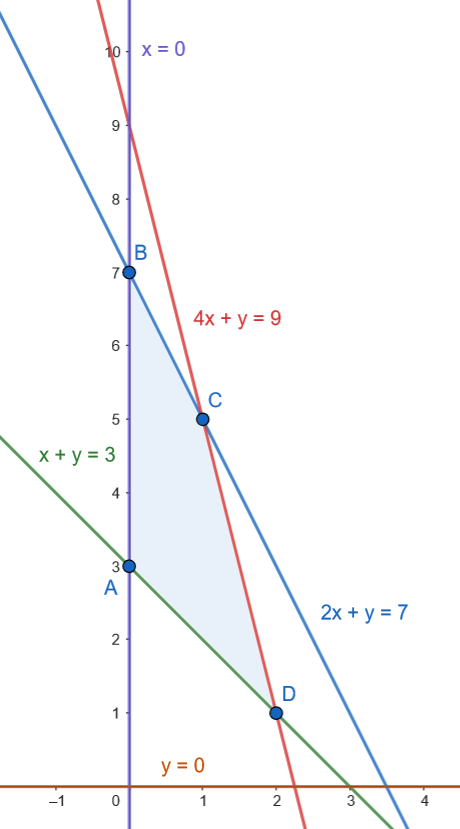 Los vértices son:
Los vértices son:
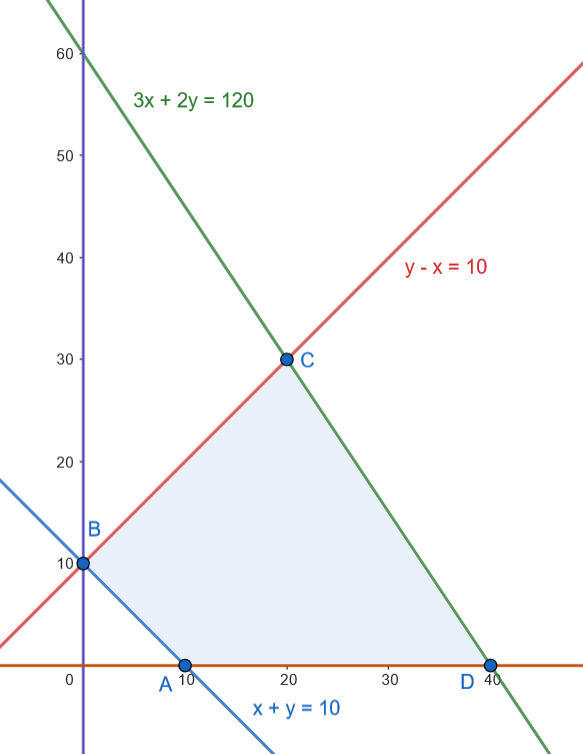 Los vértices son:
Los vértices son:
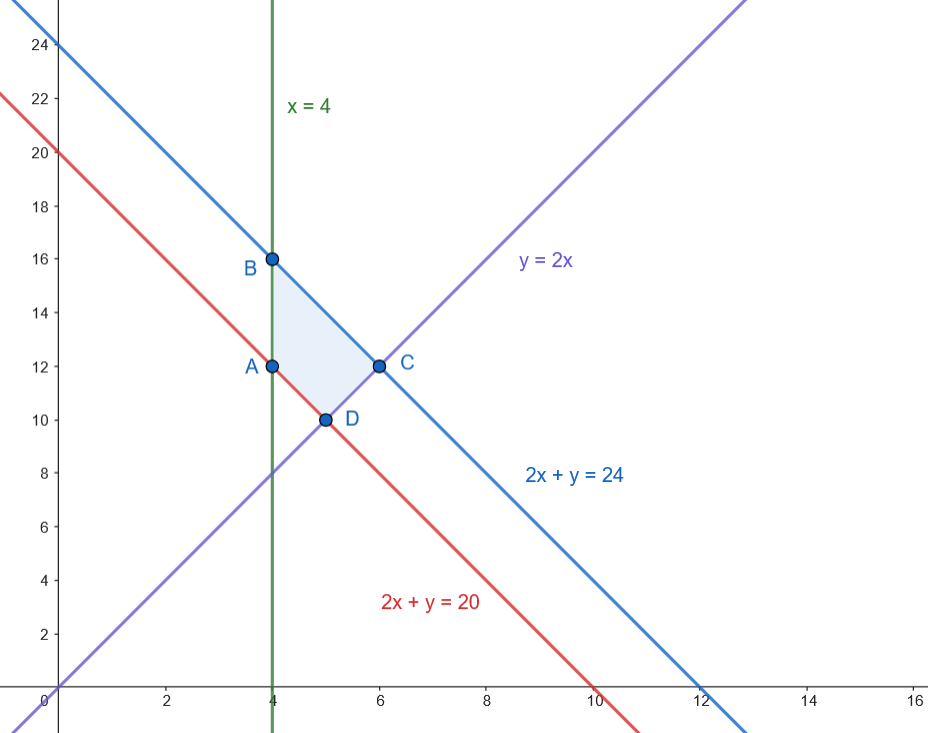 Los vértices son:
Los vértices son:
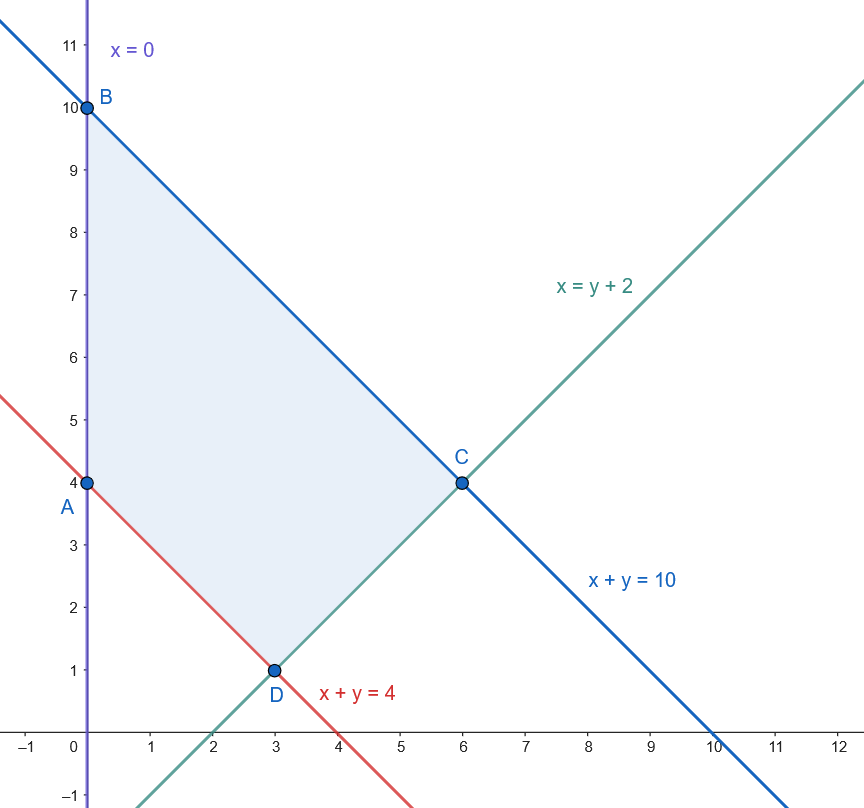 Los vértices son:
Los vértices son:
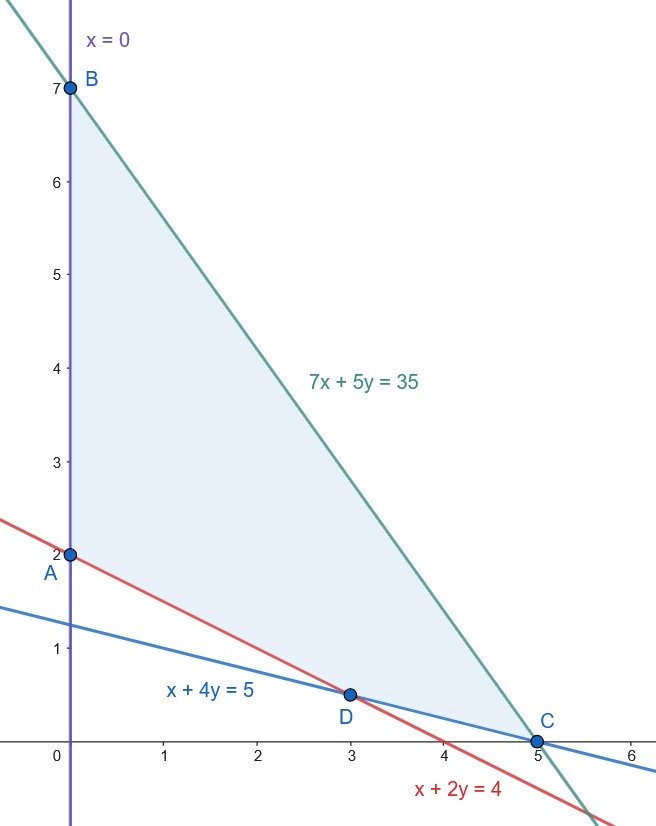 Los vértices son:
Los vértices son: