Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 1 de 2021

Ejercicio 1

La Agencia Espacial Europea contará con un presupuesto de 2,4 millones de euros para financiar misiones sobre Observación de la Tierra y para financiar programas de Transporte Espacial. Cada misión supone una inversión de 200.000 euros y cada programa, 100.000 euros. Teniendo en cuenta que en la decisión final deben superarse los 2 millones de euros de inversión y el número de misiones debe ser al menos 4, pero no más de la mitad del número de programas, ¿cuántas misiones y cuántos programas se deben llevar a cabo para obtener el máximo de la función 𝐹(𝑥,𝑦) =0,6𝑥 +0,4𝑦, con 𝑥 misiones e 𝑦 programas?

Resolución

Llamamos 𝑥 al número misiones e 𝑦 al número de programas. Las restricciones del problema son: ⎧{ { {⎨{ { {⎩200.000𝑥+100.000𝑦≤2.400.000,200.000𝑥+100.000𝑦≥2.000.000,𝑥≥4,𝑥≤𝑦2⇔⎧{ { {⎨{ { {⎩2𝑥+𝑦≤24,2𝑥+𝑦≥20,𝑥≥4,2𝑥≤𝑦. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=0,6𝑥+0,4𝑦.

Representamos la región factible. 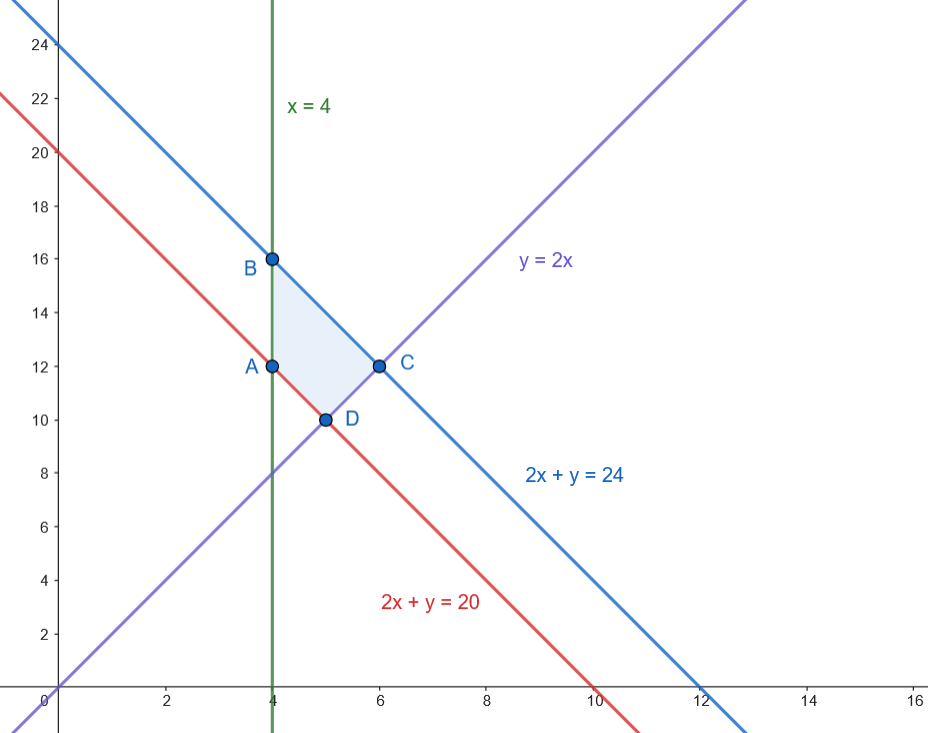Figura Los vértices son: 𝐴(4,12),𝐵(4,16),𝐶(6,12)y𝐷(5,10).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(4,12)=7,2,𝐹(𝐵)=𝐹(4,16)=8,8,𝐹(𝐶)=𝐹(6,12)=8,4,𝐹(𝐷)=𝐹(5,10)=7. Por tanto, el máximo de la función se alcanza llevando a cabo 4 misiones y 16 programas.

Ejercicio 2

Se consideran las matrices 𝐴=⎛⎜ ⎜ ⎜⎝101010101⎞⎟ ⎟ ⎟⎠,𝐵=⎛⎜ ⎜ ⎜⎝10211−1210⎞⎟ ⎟ ⎟⎠y𝐶=⎛⎜ ⎜ ⎜⎝1−31⎞⎟ ⎟ ⎟⎠.

  1. Calcule 𝐴2, 𝐴3, 𝐴4 y deduzca la expresión de 𝐴𝑛, con 𝑛 un número natural.
  2. Razone si existe la inversa de la matriz 𝐵.
  3. Razone si la ecuación matricial 𝐵𝑋 =𝐶 tiene solución y resuélvala en caso de que sea posible.

Resolución
  1. Calculamos las primeras potencias de 𝐴. 𝐴2=𝐴⋅𝐴=⎛⎜ ⎜ ⎜⎝101010101⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝101010101⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝202010202⎞⎟ ⎟ ⎟⎠,𝐴3=𝐴2⋅𝐴=⎛⎜ ⎜ ⎜⎝202010202⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝101010101⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝404010404⎞⎟ ⎟ ⎟⎠,𝐴4=𝐴3⋅𝐴=⎛⎜ ⎜ ⎜⎝404010404⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝101010101⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝808010808⎞⎟ ⎟ ⎟⎠. Por tanto, 𝐴𝑛=⎛⎜ ⎜ ⎜ ⎜⎝2𝑛−102𝑛−10102𝑛−102𝑛−1⎞⎟ ⎟ ⎟ ⎟⎠.
  2. Calculamos en primer lugar el determinante de la matriz 𝐵. |𝐵|=∣10211−1210∣=−1. Como det(𝐵) ≠0, la matriz 𝐵 es invertible.
  3. Por el apartado anterior, 𝐵 es invertible con det(𝐵) = −1. Despejamos la ecuación matricial. 𝐵𝑋=𝐶⇔𝑋=𝐵−1𝐶. Para hallar la inversa de 𝐵, calculamos primero su matriz adjunta. Adj⁡(𝐵)=⎛⎜ ⎜ ⎜⎝1−2−12−4−1−231⎞⎟ ⎟ ⎟⎠. Calculamos su inversa de la forma: 𝐵−1=1|𝐵|Adj⁡(𝐵)𝑡=−⎛⎜ ⎜ ⎜⎝12−2−2−43−1−11⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝−1−2224−311−1⎞⎟ ⎟ ⎟⎠. Por tanto, 𝑋=𝐵−1𝐶=⎛⎜ ⎜ ⎜⎝−1−2224−311−1⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝1−31⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝7−13−3⎞⎟ ⎟ ⎟⎠.

Ejercicio 3

Se considera la función 𝑓(𝑥)={𝑎𝑥+𝑏,si 𝑥<1,𝑥2−𝑏𝑥+𝑎,si 𝑥≥1.

  1. Halle el valor de 𝑏 para que 𝑓 sea continua en ℝ.
  2. Para 𝑏 =12, halle el valor de 𝑎 para que 𝑓 sea derivable en ℝ.
  3. Para 𝑎 <0 y 𝑏 =12, estudie el crecimiento y halle las abscisas de los extremos de la función 𝑓.
  4. Para 𝑎 =0 y 𝑏 =12, represente la región del plano delimitada por la gráfica de 𝑓, el eje de abscisas y las rectas 𝑥 =0 y 𝑥 =2. Calcule el área de dicha región.

Resolución
  1. Estudiamos la continuidad.
    • Si 𝑥 ≠1, 𝑓 es continua para cualquier valor de 𝑎 y 𝑏.
    • Estudiamos la continuidad en el punto de ruptura 𝑥 =1. lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡(𝑎𝑥+𝑏)=𝑎+𝑏,lím𝑥→1+⁡𝑓(𝑥)=lím𝑥→1+⁡(𝑥2−𝑏𝑥+𝑎)=1−𝑏+𝑎,𝑓(1)=1−𝑏+𝑎. Para que 𝑓 sea continua, ha de verificarse que: lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1+⁡𝑓(𝑥)=𝑓(1)⇔𝑎+𝑏=1−𝑏+𝑎⇔2𝑏=1⇔𝑏=12.
  2. Estudiamos la derivabilidad.
    • Si 𝑥 ≠1, 𝑓 es derivable para cualquier valor de 𝑎 con: 𝑓′(𝑥)={𝑎,si 𝑥<1,2𝑥−12,si 𝑥>1.
    • Estudiamos la derivabilidad en el punto de ruptura 𝑥 =1. 𝑓′−(1)=lím𝑥→1−⁡𝑓′(𝑥)=lím𝑥→1−⁡𝑎=𝑎,𝑓′+(1)=lím𝑥→1+⁡𝑓′(𝑥)=lím𝑥→1+⁡2𝑥−12=32. Para que 𝑓 sea derivable, ha de verificarse que: 𝑓′−(1)=𝑓′+(1)⇔𝑎=32.
  3. Para hallar los puntos críticos, igualamos las dos ramas de la derivada a cero.
    • Si 𝑥 <1, 𝑓′(𝑥)=𝑎≠0.
    • Si 𝑥 >1, 𝑓′(𝑥)=0⇔2𝑥−12=0⇔𝑥=14∉(1,+∞).
    Así que la función no tiene ningún punto crítico. Consideramos 𝑥 =1 por ser no derivable. Estudiamos el signo de la derivada.
    ( −∞,1) (1, +∞)
    signo de 𝑓′ − +
    monotonía de 𝑓 → →
    Por tanto, 𝑓 es creciente en (1, +∞) y decreciente en ( −∞,1). Además, tiene un mínimo relativo en 𝑥 =1.
  4. Representamos la región. Figura Calculamos el área. ∫1012𝑑𝑥+∫21(𝑥2−12𝑥)𝑑𝑥=[12𝑥]10+[13𝑥3−14𝑥2]21=12+83−1−(13−14)=2512𝑢2.

Ejercicio 4

La cotización en bolsa de una empresa en un determinado dia viene expresada, en euros, por la función 𝑐(𝑡), con 𝑡 ∈[0,24], medido en horas. La variación instantánea de esta función es la derivada de 𝑐, que viene dada por 𝑐′(𝑡) =0,03𝑡2 −0,9𝑡 +6, con 𝑡 ∈(0,24).

  1. Estudie los intervalos en los que la función 𝑐 es creciente.
  2. Analice los puntos críticos de la función 𝑐, indicando en cuáles se alcanza el máximo y el mínimo relativos.
  3. Halle la expresión analítica de la función 𝑐, sabiendo que la cotización en bolsa de la empresa era de 50 euros en el instante inicial.

Resolución
  1. Para hallar los puntos críticos, igualamos la derivada de 𝑐 a cero. 𝑐′(𝑡)=0⇔0,03𝑡2−0,9𝑡+6=0⇔𝑡2−30𝑡+200=0⇔{𝑡=10,𝑡=20. Estudiamos el signo de la derivada.
    (0,10) (10,20) (20,24)
    signo de 𝑐′ + − +
    monotonía de 𝑐 → → →
    Por tanto, 𝑓 es creciente en (0,10) ∪(20,24).
  2. Los puntos críticos de 𝑐 se encuentran en 𝑡 =10 y 𝑡 =20. El máximo relativo se alcanza en 𝑡 =10 y el mínimo relativo en 𝑡 =20.
  3. En primer lugar, hallamos la función 𝑐 integrando. 𝑐(𝑡)=∫𝑐′(𝑡)𝑑𝑡=∫(0,03𝑡2−0,9𝑡+6)𝑑𝑡=0,01𝑡3−0,45𝑡2+6𝑡+𝐾. Como la cotización al inicio era de 50 euros, ha de verificarse que: 𝑐(0)=50⇔𝐾=50. Por tanto, 𝑐(𝑡)=0,01𝑡3−0,45𝑡2+6𝑡+50.

Ejercicio 5

Una empresa dedicada a la fabricación de coches lanza al mercado un nuevo modelo que fabrica en tres plantas diferentes, A, B y C. La planta A produce el 45% de los vehículos, la planta B el 21% y el resto los produce la planta C. Se ha detectado un defecto en la colocación del airbag, que afecta al 1% de los coches procedentes de la planta A, al 3% de los procedentes de la planta B y al 2% de los de la planta C. Se selecciona un coche al azar de este nuevo modelo.

  1. ¿Cuál es la probabilidad de que no sea defectuoso y proceda de la planta C?
  2. Si el coche elegido no es defectuoso, ¿cuál es la probabilidad de que proceda de la planta A?

Resolución

Llamamos 𝐴 a proceder de la planta A, 𝐵 a proceder de la planta B, 𝐶 a proceder de la planta C y 𝐷 a ser defectuoso. Podemos hacer un diagrama de árbol.

𝐷
0,01←←←←←←←←←←←→
𝐴
0,45←←←←←←←←←←←→ 0,99←←←←←←←←←←←→
𝐷𝑐
𝐷
0,03←←←←←←←←←←←→
0,21←←←←←←←←←←←→ 𝐵
0,97←←←←←←←←←←←→
𝐷𝑐
𝐷
0,34←←←←←←←←←←←→ 0,02←←←←←←←←←←←→
𝐶
0,98←←←←←←←←←←←→
𝐷𝑐
  1. La probabilidad de que no sea defectuoso y proceda de la planta C es: 𝑃(𝐷𝑐∩𝐶)=𝑃(𝐶)⋅𝑃(𝐷𝑐|𝐶)=0,34⋅0,98=0,3332.
  2. Por el teorema de la probabilidad total, la probabilidad de que el coche elegido no sea defectuoso es: 𝑃(𝐷𝑐)=𝑃(𝐷𝑐∩𝐴)+𝑃(𝐷𝑐∩𝐵)+𝑃(𝐷𝑐∩𝐶)=𝑃(𝐴)⋅𝑃(𝐷𝑐|𝐴)+𝑃(𝐵)⋅𝑃(𝐷𝑐|𝐵)+𝑃(𝐶)⋅𝑃(𝐷𝑐|𝐶)==0,45⋅0,99+0,21⋅0,97+0,34⋅0,98=0,9824. Por tanto, la probabilidad de que el coche elegido proceda de la planta A sabiendo que no es defectuoso es: 𝑃(𝐴|𝐷𝑐)=𝑃(𝐴∩𝐷𝑐)𝑃(𝐷𝑐)=𝑃(𝐴)⋅𝑃(𝐷𝑐|𝐴)𝑃(𝐷𝑐)=0,45⋅0,990,9824≈0,4535.

Ejercicio 6

La probabilidad de que una persona sana se contagie de otra enferma por un virus es del 80% si coinciden en una reunión.

  1. Si una persona enferma se reúne con dos personas sanas, teniendo en cuenta que contagiar a distintas personas son sucesos independientes entre sí, ¿cuál es la probabilidad de que se contagien las dos personas a la vez? ¿Cuál es la probabilidad de que se contagie alguna de ellas?
  2. Una prueba para detectar la enfermedad da el resultado correcto en el 90% de los casos cuando se le aplica a personas contagiadas y da falsos positivos en el 5% de los casos cuando se aplica a personas sanas. Si una persona sana se reúne con una enferma y resulta positivo en una prueba posterior, ¿qué probabilidad hay de que se haya contagiado en la reunión?

Resolución

Llamamos 𝐶 a ser contagiado y 𝐴 a resultar positivo en la prueba. Sabemos que 𝑃(𝐶) =0,8.

  1. Como son sucesos independientes, la probabilidad de que se contagien las dos personas a la vez es: 𝑃(𝐶1∩𝐶2)=𝑃(𝐶1)⋅𝑃(𝐶2)=0,8⋅0,8=0,64. La probabilidad de que se contagie alguna de ellas viene dada por: 𝑃(𝐶1∪𝐶2)=𝑃(𝐶1)+𝑃(𝐶2)−𝑃(𝐶1∩𝐶2)=0,8+0,8−0,64=0,96.
  2. Podemos hacer un diagrama de árbol.
    𝐴
    0,9←←←←←←←←←←→
    𝐶
    0,8←←←←←←←←←←→ 0,1←←←←←←←←←←→
    𝐴𝑐
    𝐴
    0,2←←←←←←←←←←→ 0,05←←←←←←←←←←←→
    𝐶𝑐
    0,95←←←←←←←←←←←→
    𝐴𝑐
    Por el teorema de la probabilidad total, la probabilidad de que una persona resulte positivo en la prueba es: 𝑃(𝐴)=𝑃(𝐴∩𝐶)+𝑃(𝐴∩𝐶𝑐)=𝑃(𝐶)⋅𝑃(𝐴|𝐶)+𝑃(𝐶𝑐)⋅𝑃(𝐴|𝐶𝑐)=0,8⋅0,9+0,2⋅0,05=0,73. Por tanto, la probabilidad de que una persona se haya contagiado en la reunión sabiendo que ha resultado positivo es: 𝑃(𝐶|𝐴)=𝑃(𝐶∩𝐴)𝑃(𝐴)=𝑃(𝐶)⋅𝑃(𝐴|𝐶)𝑃(𝐴)=0,8⋅0,90,73≈0,9863.

Ejercicio 7

Para un estudio acerca del uso del transporte público en una ciudad, se selecciona una muestra aleatoria de 500 individuos, obteniéndose que 175 de ellos lo usan.

  1. Halle un intervalo de confianza al 94% para estimar la proporción real de individuos que usan el transporte público en esa ciudad.
  2. Manteniendo la proporción muestral, ¿cuántos individuos se deberían seleccionar como mínimo, para que, con un nivel de confianza del 97%, la proporción muestral difiera de la proporción real a lo sumo en un 2%?

Resolución
  1. Como 175 individuos de 𝑛 =500 usan el transporte público, la proporción muestral es: 𝑝=175500=0,35. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 94%, entonces: 𝛼=1−0,94=0,06⇒1−𝛼2=1−0,062=0,97⇒𝑧𝛼/2=1,885. Por tanto, el intervalo de confianza para estimar la proporción de individuos que usan el transporte público con un nivel de confianza del 94% es: 𝐼=(0,35−1,885⋅√0,35⋅(1−0,35)500,0,35+1,885⋅√0,35⋅(1−0,35)500)≈(0,3098;0,3902).
  2. Si el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=2,17⋅√0,35⋅(1−0,35)𝑛=2,17⋅√0,2275𝑛. Si se quiere el error sea inferior a 0,02, entonces: 2,17⋅√0,2275𝑛=0,02⇔√0,2275𝑛=0,022,17⇔0,2275𝑛=0,0222,172⇔𝑛=0,2275⋅2,1720,022≈2.678,1869. Por tanto, el número mínimo de individuos de la muestra debe ser 2.679.

Ejercicio 8

La estatura de las mujeres de una población sigue una ley Normal de media desconocida y desviación típica 7 cm.

  1. Se toma una muestra aleatoria de 300 mujeres de esta población, que da una estatura media de 168 cm. Construya un intervalo de confianza al 97% para estimar la estatura media de las mujeres de esta población.
  2. Calcule el tamaño mínimo que debe tener una muestra de esta población para que, con un nivel de confianza del 94%, el error máximo cometido al estimar la estatura media de las mujeres de esa población sea inferior a 1,2 cm.

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar la estatura media de las mujeres con un nivel de confianza del 97% es: 𝐼=(168−2,17⋅7√300,168+2,17⋅7√300)≈(167,1230;168,8770).
  2. Si el nivel de confianza es del 94%, entonces: 𝛼=1−0,94=0,06⇒1−𝛼2=1−0,062=0,97⇒𝑧𝛼/2=1,885. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=1,885⋅7√𝑛=13,195√𝑛. Si se quiere que el error máximo sea inferior a 1,2, entonces: 13,195√𝑛=1,2⇔√𝑛=13,1951,2⇔𝑛=13,19521,22≈120,9084. Por tanto, el tamaño mínimo de la muestra debe ser de 121 personas.