Ejercicio 2: Junio de 2025
Un periódico digital ha publicado una noticia de última hora.
El número de personas que han visto la noticia
- Estudie la monotonía y curvatura de la función
𝑁 - Represente gráficamente la función
𝑁 - ¿Cuánto tiempo ha debido de pasar para que la noticia haya sido vista por 450.000 personas?
-
La velocidad de difusión de la noticia (número de personas por hora que han visto la publicación) es
𝑁 ′ ( 𝑡 ) 𝑁 ′ ( 𝑡 ) 𝑡 = 1 𝑡 = 1 0
Resolución
-
En primer lugar, hallamos las dos primeras derivadas de la función $N$.
\begin{align}
N'(t) & = 500.000 \cdot (-e^{-0,2t}) \cdot (-0,2) = 100.000e^{-0,2t}, \\
N''(t) & = 100.000e^{-0,2t} \cdot (-0,2) = -20.000e^{-0,2t}.
\end{align}
- Observamos que $N'(t) > 0$ para $t > 0$, así que $N$ es creciente en todo su dominio.
- Observamos que $N''(t) < 0$ para $t > 0$, así que $N$ es cóncava en todo su dominio.
-
Veamos si la gráfica de la función tiene asíntota horizontal para estudiar su tendencia.
$$\lim_{t \to +\infty} N(t) = \lim_{t \to +\infty} 500.000(1 - e^{-0,2t}) = 500.000.$$
Por tanto, la recta $y = 500.000$ es una asíntota horizontal.
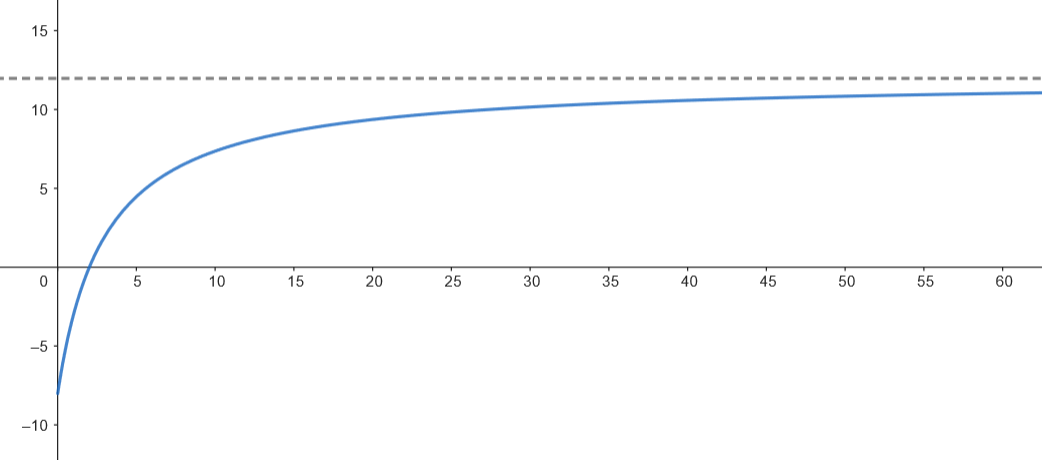
Representamos gráficamente la función usando esta información.
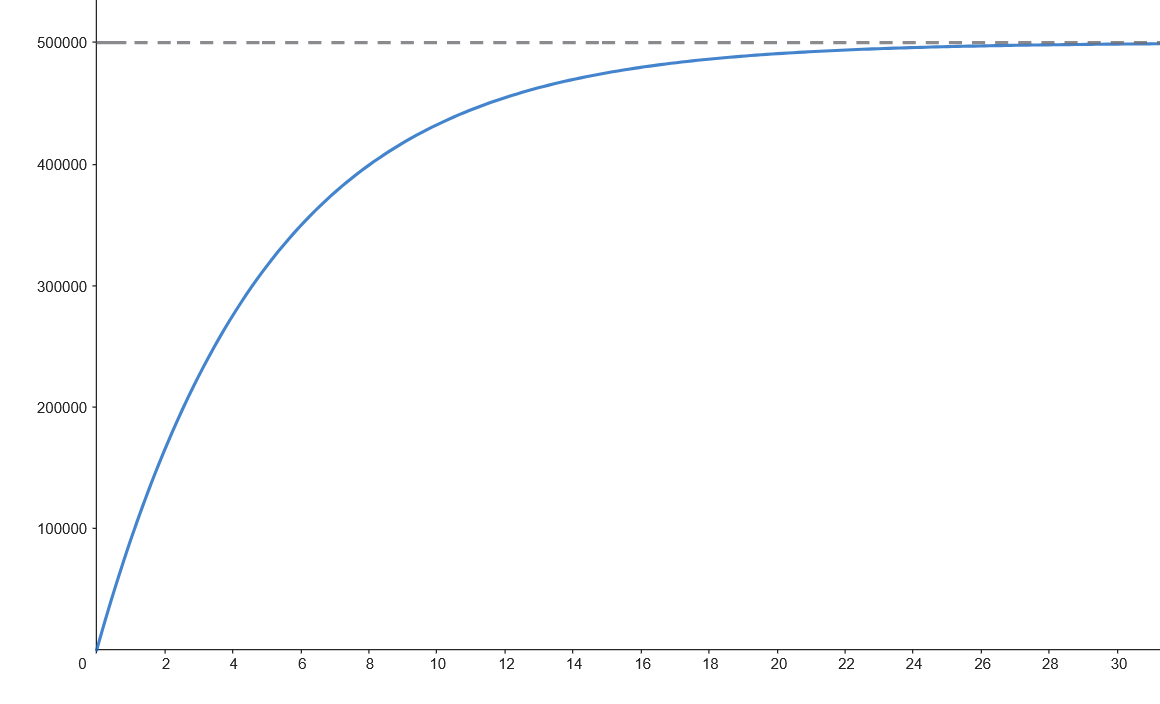 Podemos observar que el número de personas que ven la noticia aumenta rápidamente en las primeras horas y se va acercando a 500.000, cada vez con menor velocidad.
Podemos observar que el número de personas que ven la noticia aumenta rápidamente en las primeras horas y se va acercando a 500.000, cada vez con menor velocidad.
- Para que la noticia haya sido vista por 450.000 personas ha de verificarse que: \begin{align} N(t) = 450.000 & \Leftrightarrow 500.000(1 - e^{-0,2t}) = 450.000 \Leftrightarrow 1 - e^{-0,2t} = \frac{9}{10} \Leftrightarrow e^{-0,2t} = \frac{1}{10} \Leftrightarrow \\ & \Leftrightarrow -0,2t = \ln\left(\frac{1}{10}\right) \Leftrightarrow t = -\frac{\ln\left(\frac{1}{10}\right)}{0,2} = 5\ln(10) \approx 11,5129. \end{align} Por tanto, han debido de pasar un poco más de 11 horas y media.
- Calculamos el valor de la derivada en los dos instantes. $$N'(1) \approx 81.873,0753, \quad N'(10) \approx 13.533,5283.$$ Observamos que la velocidad de difusión de la noticia se reduce en gran medida con el paso de las horas.
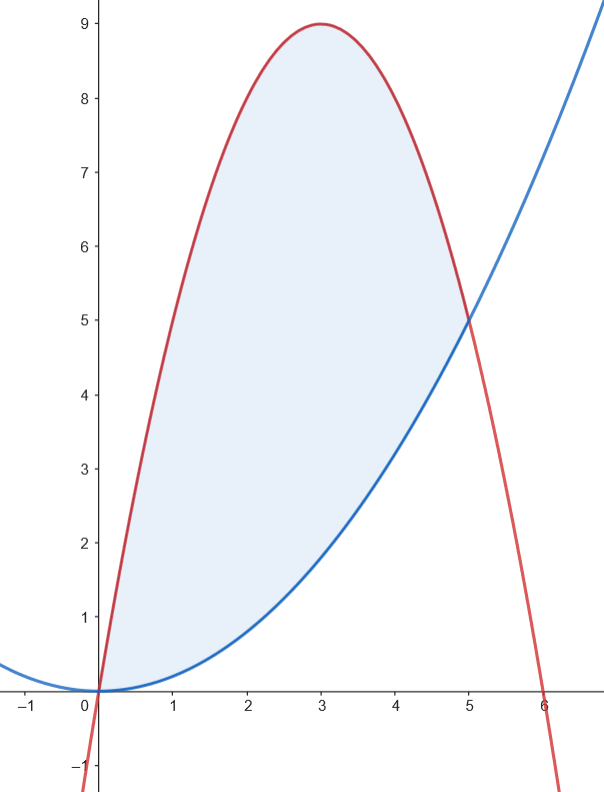
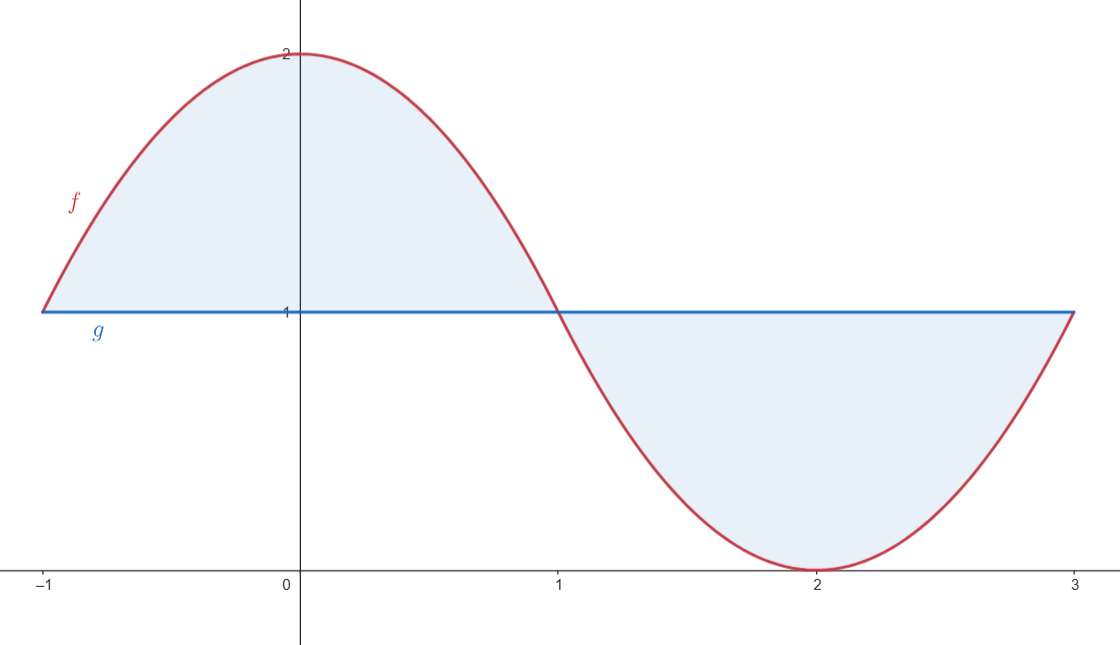 Como los dos recintos tienen la misma superficie, podemos calcular el área como
\begin{align}
& 2 \int_{-1}^1 (f(x) - g(x))dx = 2 \int_{-1}^1 (2-x^2 - 1)dx = 2 \int_{-1}^1 (-x^2 + 1)dx = 2 \left[-\frac{1}{3}x^3 + x\right]_{-1}^1 = \\
& = 2 \left(-\frac{1}{3} + 1 - \left(\frac{1}{3} - 1\right)\right) = \frac{8}{3} \; u^2.
\end{align}
Como los dos recintos tienen la misma superficie, podemos calcular el área como
\begin{align}
& 2 \int_{-1}^1 (f(x) - g(x))dx = 2 \int_{-1}^1 (2-x^2 - 1)dx = 2 \int_{-1}^1 (-x^2 + 1)dx = 2 \left[-\frac{1}{3}x^3 + x\right]_{-1}^1 = \\
& = 2 \left(-\frac{1}{3} + 1 - \left(\frac{1}{3} - 1\right)\right) = \frac{8}{3} \; u^2.
\end{align}
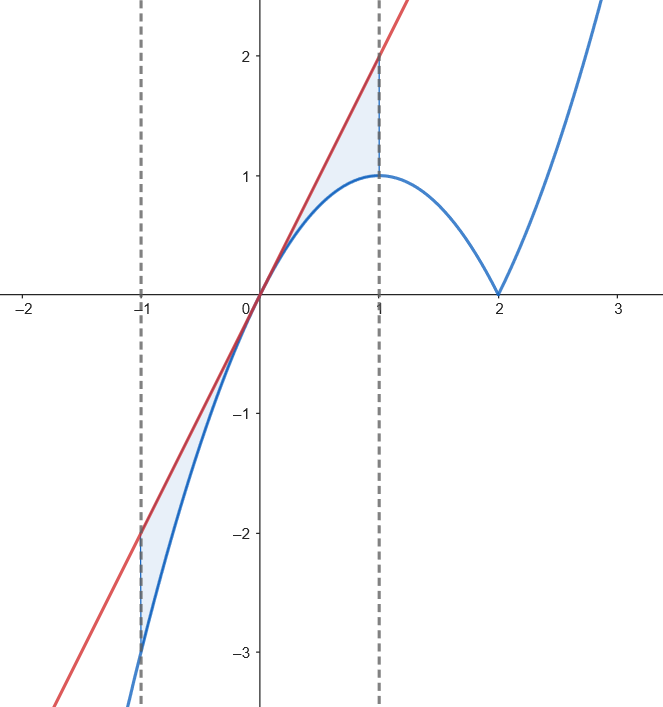 Calculamos el área.
$$\int_{-1}^1 (2x - (x^2 + 2x))dx = \int_{-1}^1 x^2 dx = \left[\frac{1}{3}x^3\right]_{-1}^1 = \frac{1}{3} - \left(-\frac{1}{3}\right) = \frac{2}{3} \; u^2.$$
Calculamos el área.
$$\int_{-1}^1 (2x - (x^2 + 2x))dx = \int_{-1}^1 x^2 dx = \left[\frac{1}{3}x^3\right]_{-1}^1 = \frac{1}{3} - \left(-\frac{1}{3}\right) = \frac{2}{3} \; u^2.$$
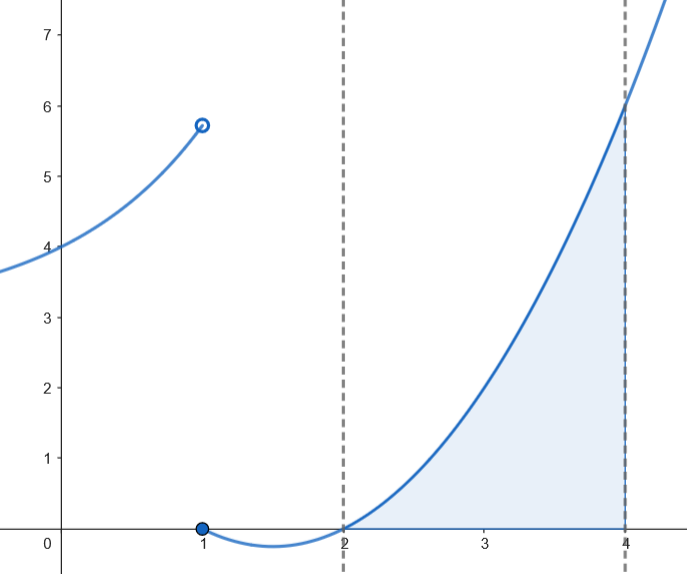 Calculamos el área.
$$\int_2^4 f(x)dx = \int_2^4 (x^2 - 3x + 2)dx = \left[\frac{1}{3}x^3 - \frac{3}{2}x^2 + 2x\right]_2^4 = \frac{64}{3} - 24 + 8 - \left(\frac{8}{3} - 6 + 4\right) = \frac{14}{3} \; u^2.$$
Calculamos el área.
$$\int_2^4 f(x)dx = \int_2^4 (x^2 - 3x + 2)dx = \left[\frac{1}{3}x^3 - \frac{3}{2}x^2 + 2x\right]_2^4 = \frac{64}{3} - 24 + 8 - \left(\frac{8}{3} - 6 + 4\right) = \frac{14}{3} \; u^2.$$
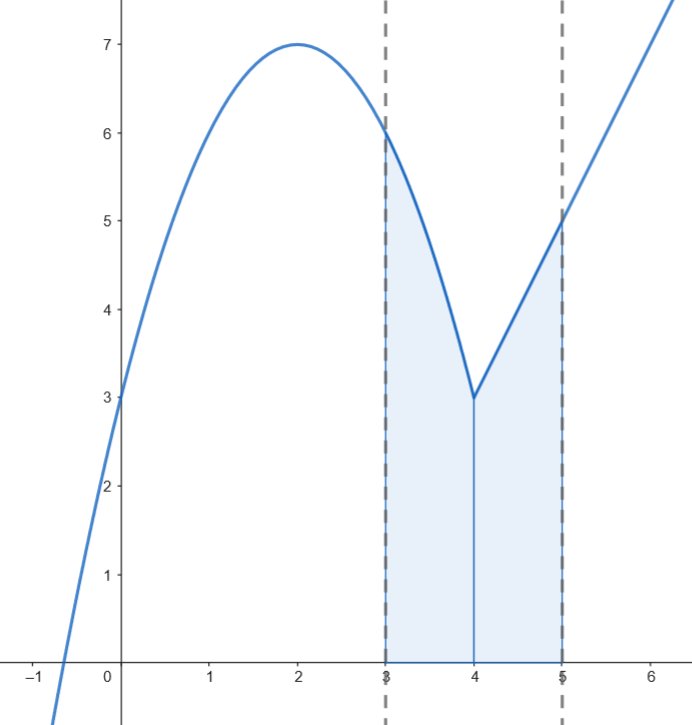 Calculamos el área.
\begin{align}
& \int_{3}^4 (-x^2 + 4x + 3)dx + \int_4^5 (2x - 5)dx = \left[-\frac{1}{3}x^3 + 2x^2 + 3x\right]_3^4 + \Big[x^2 - 5x\Big]_4^5 = \\
& -\frac{64}{3} + 32 + 12 - (-9 + 18 + 9) + 25 - 25 - (16 - 20) = \frac{26}{3} \; u^2.
\end{align}
Calculamos el área.
\begin{align}
& \int_{3}^4 (-x^2 + 4x + 3)dx + \int_4^5 (2x - 5)dx = \left[-\frac{1}{3}x^3 + 2x^2 + 3x\right]_3^4 + \Big[x^2 - 5x\Big]_4^5 = \\
& -\frac{64}{3} + 32 + 12 - (-9 + 18 + 9) + 25 - 25 - (16 - 20) = \frac{26}{3} \; u^2.
\end{align}
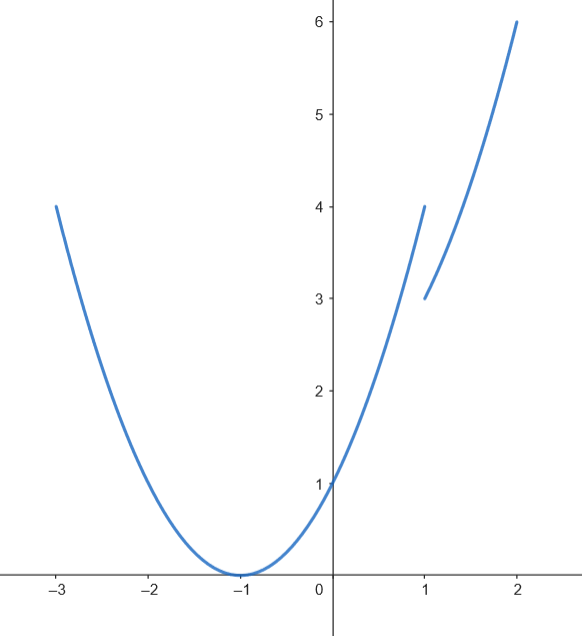 Podemos representar gráficamente el recinto acotado limitado por la gráfica de $f$, el eje $X$ y las rectas $x = -2$ y $x = 1.$
Podemos representar gráficamente el recinto acotado limitado por la gráfica de $f$, el eje $X$ y las rectas $x = -2$ y $x = 1.$
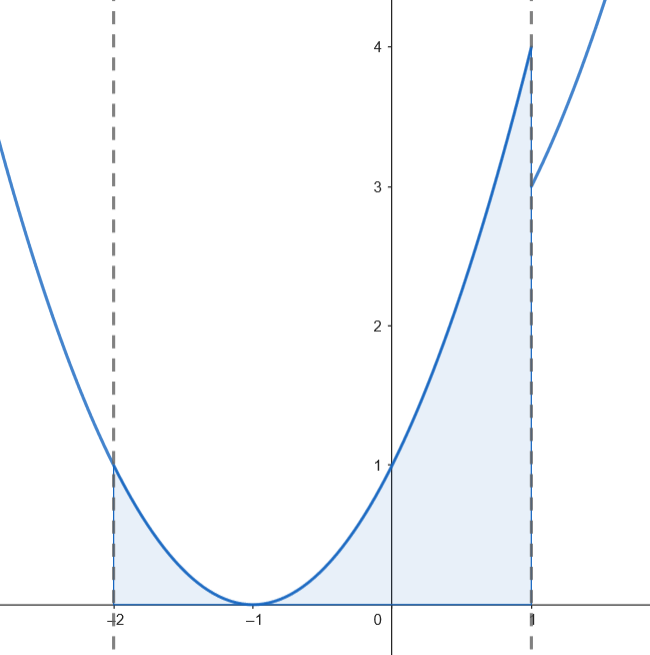 Calculamos el área.
\begin{align}
& \int_{-2}^1 f(x)dx = \int_{-2}^1 (x+1)^2 dx = \int_{-2}^1 (x^2 + 2x + 1)dx = \left[\frac{1}{3}x^3 + x^2 + x\right]_{-2}^1 = \\
& = \frac{1}{3} + 1 + 1 - \left(-\frac{8}{3} + 4 - 2\right) = 3 \; u^2.
\end{align}
Calculamos el área.
\begin{align}
& \int_{-2}^1 f(x)dx = \int_{-2}^1 (x+1)^2 dx = \int_{-2}^1 (x^2 + 2x + 1)dx = \left[\frac{1}{3}x^3 + x^2 + x\right]_{-2}^1 = \\
& = \frac{1}{3} + 1 + 1 - \left(-\frac{8}{3} + 4 - 2\right) = 3 \; u^2.
\end{align}
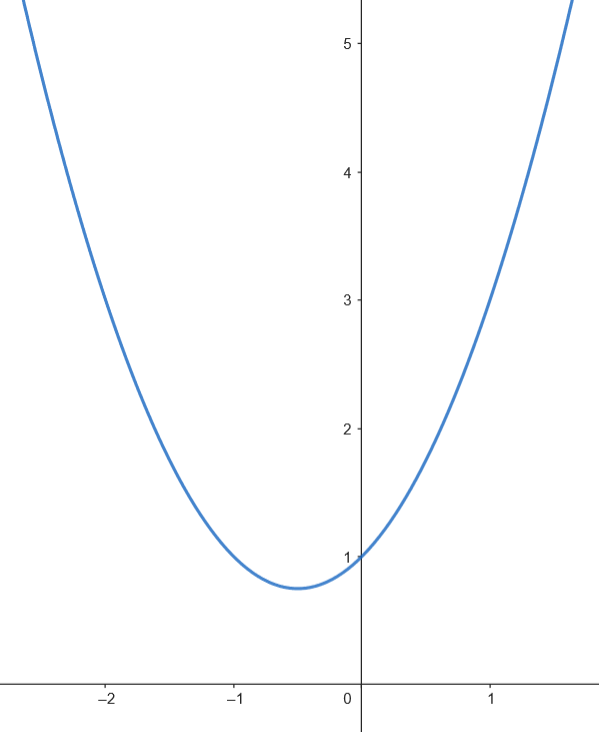
 Calculamos el área.
$$\int_{-\frac{1}{2}}^0 h(x)dx = \int_{-\frac{1}{2}}^0 (x^2+x+1)dx = \left[\frac{1}{3}x^3 + \frac{1}{2}x^2 + x\right]_{-\frac{1}{2}}^0 = -\left(-\frac{1}{24} + \frac{1}{8} - \frac{1}{2}\right) = \frac{5}{12} \; u^2.$$
Calculamos el área.
$$\int_{-\frac{1}{2}}^0 h(x)dx = \int_{-\frac{1}{2}}^0 (x^2+x+1)dx = \left[\frac{1}{3}x^3 + \frac{1}{2}x^2 + x\right]_{-\frac{1}{2}}^0 = -\left(-\frac{1}{24} + \frac{1}{8} - \frac{1}{2}\right) = \frac{5}{12} \; u^2.$$