Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 2 de 2023

Ejercicio 1

Una conservera fabrica latas de pisto con tomate, cebolla y pimiento siguiendo dos recetas distintas. La matriz (500300200600100300) indica los gramos necesarios de cada producto para conseguir una lata de cada receta. Se dispone de dos proveedores, siendo la matriz de precios en euros por kilo de cada producto (0,50,40,60,40,50,7). Los costes de producción de cada receta en euros por lata vienen dados por la matriz (0,110,09). Los costes de transporte en euros por lata según cada proveedor vienen dados por la matriz (0,020,03). La conservera quiere obtener un beneficio de 5 céntimos por lata. Una distribuidora compra 11.000 latas de la primera receta, siendo 5.000 del primer proveedor, y otras 11.000 de la segunda receta, siendo 6.000 del primer proveedor. ¿Cuánto debe cobrar la conservera por el pedido de esta distribuidora?

Resolución

Los costes están divididos en costes de los productos, costes de producción y costes de transporte.

En primer lugar, pasamos la matriz de gramos necesarios por lata a kilogramos. (500300200600100300)→(0,50,30,20,60,10,3). El producto de matrices (0,50,30,20,60,10,3)⎛⎜ ⎜ ⎜⎝0,50,40,40,50,60,7⎞⎟ ⎟ ⎟⎠=(0,490,490,520,5) recoge el precio en euros de cada lata por receta y proveedor, donde las filas indican las recetas y las columnas los proveedores. Por otro lado, la matriz que recoge las latas compradas por receta y proveedor es (5.0006.0006.0005.000). Así que los elementos de la diagonal principal del producto (5.0006.0006.0005.000)(0,490,520,490,5)=(5.3905.6005.3905.620) representan el coste de los productos para cada receta. Por tanto, el coste de los productos es 5.390+5.620=11.010€.

Se compran 11.000 latas de cada receta, así que el coste de producción viene dado por el producto de matrices (11.00011.000)(0,110,09)=2.200€.

De igual forma, el coste de transporte viene dado por (11.00011.000)(0,020,03)=550€.

En conclusión, el coste total es 11.010+2.200+550=13.760€. Como se quiere obtener un beneficio de 5 céntimos por lata y se compran 22.000 latas, el beneficio buscado será de 0,05⋅22.000=1.100€. Por tanto, la conservera debe cobrar 13.760+1.100=14.860€.

Ejercicio 2

Una compañía de transporte marítimo de mercancías dispone de dos barcos 𝐵1 y 𝐵2 para realizar una determinada ruta, durante un año, entre dos ciudades costeras europeas. El barco 𝐵1 no puede realizar más de 14 viajes y debe realizar tantos viajes o más que el barco 𝐵2. Entre los dos barcos deben realizar al menos 10 viajes y como mucho 24. La compañía obtiene unos beneficios de 15.000€ por cada viaje del barco 𝐵1 y 17.000€ por cada viaje del barco 𝐵2. Halle el número de viajes que debe realizar cada barco para que el beneficio obtenido por la empresa sea máximo y obtenga dicho beneficio.

Resolución

Llamamos 𝑥 al número de viajes realizados por el barco 𝐵1 en un año e 𝑦 al de los realizados por 𝐵2.

Las restricciones del problema son: ⎧{ { { {⎨{ { { {⎩𝑥≤14,𝑥≥𝑦,𝑥+𝑦≥10,𝑥+𝑦≤24,𝑦≥0. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=15.000𝑥+17.000𝑦.

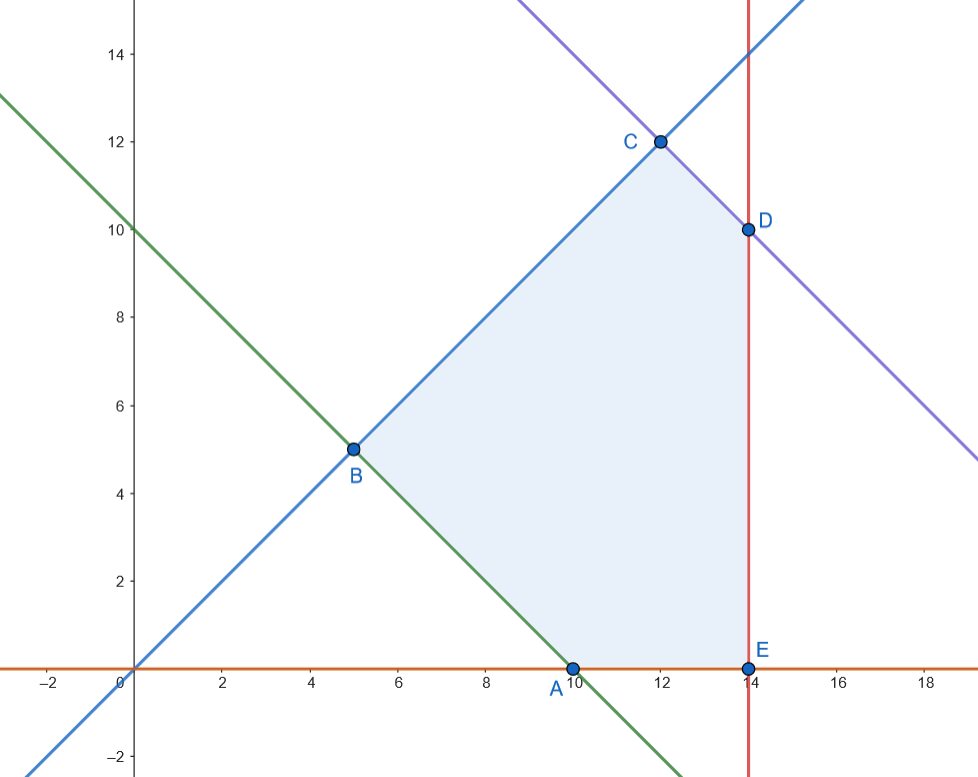Representamos la región factible. Figura Los vértices son: 𝐴(10,0),𝐵(5,5),𝐶(12,12),𝐷(14,10),𝐸(14,0).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(10,0)=150.000,𝐹(𝐵)=𝐹(5,5)=160.000,𝐹(𝐶)=𝐹(12,12)=384.000,𝐹(𝐷)=𝐹(14,10)=380.000,𝐹(𝐸)=𝐹(14,0)=210.000. Por tanto, el valor máximo de los beneficios se alcanza realizando 12 viajes con cada barco en un año, con unas ganancias de 384.000€.

Ejercicio 3

  1. Calcule las derivadas de las siguientes funciones: 𝑓(𝑥)=(−7+𝑥2)3𝑒5−𝑥,𝑔(𝑥)=ln⁡(𝑥4−2𝑥2)8−𝑥3.
  2. Represente gráficamente la región acotada comprendida entre la recta 𝑦 = −2𝑥 +6 y la parábola 𝑦 = −𝑥2 +2𝑥 +3 y calcule su área.

Resolución
    • Calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=3(−7+𝑥2)2⋅2𝑥⋅𝑒5−𝑥+(−7+𝑥2)3⋅𝑒5−𝑥⋅(−1)=6𝑥(𝑥2−7)2𝑒5−𝑥−(𝑥2−7)3𝑒5−𝑥==(𝑥2−7)2(−𝑥2+6𝑥+7)𝑒5−𝑥.
    • Calculamos la derivada de la función 𝑔. 𝑔′(𝑥)=1𝑥4−2𝑥2⋅(4𝑥3−4𝑥)⋅(8−𝑥3)−ln⁡(𝑥4−2𝑥2)⋅(−3𝑥2)(8−𝑥3)2=(4𝑥3−4𝑥)(8−𝑥3)𝑥4−2𝑥2+3𝑥2ln⁡(𝑥4−2𝑥2)(8−𝑥3)2.
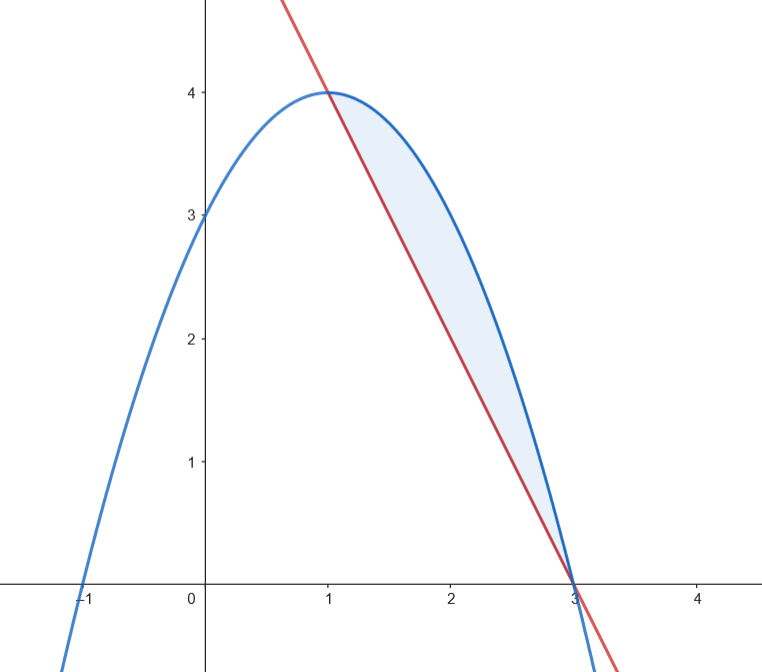  2. Llamamos 𝑓(𝑥) = −2𝑥 +6 y 𝑔(𝑥) = −𝑥2 +2𝑥 +3. En primer lugar, hallamos los puntos de corte de 𝑓 y 𝑔. 𝑓(𝑥)=𝑔(𝑥)⇔−2𝑥+6=−𝑥2+2𝑥+3⇔𝑥2−4𝑥+3=0⇔{𝑥=1,𝑥=3. Así que los puntos de corte son (1,4) y (3,0). Observamos además que el vértice de la parábola es (1,4). Representamos el recinto acotado limitado por ambas funciones. Figura Calculamos el área del recinto. ∫31(𝑔(𝑥)−𝑓(𝑥))𝑑𝑥=∫31(−𝑥2+2𝑥+3−(−2𝑥+6))𝑑𝑥=∫31(−𝑥2+4𝑥−3)𝑑𝑥=[−13𝑥3+2𝑥2−3𝑥]31==−9+18−9−(−13+2−3)=43𝑢2.

Ejercicio 4

La temperatura en el interior de un equipo de refrigeración durante un día que sufrió un corte de energía viene dada por la función 𝑓 expresada en grados centígrados y el tiempo 𝑡 en horas: 𝑓(𝑡)=⎧{ {⎨{ {⎩−9,si 0≤𝑡≤1,−𝑡2+12𝑡−20,si 1<𝑡<11,−9,si 11≤𝑡≤24.

  1. Estudie la continuidad de 𝑓.
  2. Represente gráficamente la función 𝑓.
  3. Conteste razonadamente a qué hora se produjo el corte de energía y cuánto duró dicho corte.
  4. El equipo de refrigeración se utiliza para conservar sueros y vacunas. Los sueros se estropean si se alcanzan temperaturas de 20°C en algún momento. Las vacunas se estropean si están por encima de 0°C durante más de seis horas. Razone si alguno de esos productos se estropeó ese día.

Resolución
  1. Estudiamos la continuidad de la función 𝑓.
    • Si 𝑡 ∈[0,24] con 𝑡 ≠1 y 𝑡 ≠11, 𝑓 es continua.
    • Estudiamos la continuidad para el punto de ruptura 𝑡 =1. lím𝑡→1−⁡𝑓(𝑡)=lím𝑡→1−−9=−9,lím𝑡→1+⁡𝑓(𝑡)=lím𝑡→1+−𝑡2+12𝑡−20=−9,𝑓(1)=−9. Observamos que lím𝑡→1−⁡𝑓(𝑡)=lím𝑡→1+⁡𝑓(𝑡)=𝑓(1). Así que 𝑓 es continua en 𝑡 =1.
    • Estudiamos la continuidad para el punto de ruptura 𝑡 =11. lím𝑡→11−⁡𝑓(𝑡)=lím𝑡→11−−𝑡2+12𝑡−20=−9,lím𝑡→11+⁡𝑓(𝑡)=lím𝑡→11+−9=−9,𝑓(11)=−9. Observamos que lím𝑡→11−⁡𝑓(𝑡)=lím𝑡→11+⁡𝑓(𝑡)=𝑓(11). Así que 𝑓 es continua en 𝑡 =11.
    Por tanto, 𝑓 es continua en [0,24].
  2. Representamos gráficamente la función. Observamos que la parábola tiene vértice (6,16). Figura
  3. El corte de energía se produjo al cabo de 1 hora, que es el momento en el que la temperatura comenzó a aumentar. Por otro lado, la energía se restableció a las 6 horas, en el máximo absoluto, el momento en el que la temperatura empezó a disminuir de nuevo. Por tanto, el corte de energía duró 5 horas.
  4. Los sueros no se estropearon, puesto que la temperatura máxima que se alcanzó fue de 16ºC. Por otro lado, como la temperatura estuvo por encima de los 0ºC durante 8 horas (de 𝑡 =2 a 𝑡 =10), las vacunas sí se estropearon.

Ejercicio 5

En una encuesta realizada en un instituto sobre los hábitos de los estudiantes en su tiempo libre, el 80% de los encuestados dedica el tiempo libre a enviar mensajes con el móvil o a jugar a videojuegos, el 45% realiza ambas cosas y el 40% no juega a videojuegos. Si se elige un estudiante de ese instituto al azar, calcule la probabilidad de que dedique su tiempo libre a:

  1. Enviar mensajes con el móvil y no jugar a videojuegos.
  2. Jugar a videojuegos sabiendo que no envía mensajes con el móvil.
  3. Hacer solamente una de las dos cosas.
  4. No hacer ninguna de las dos cosas.

Resolución

Llamamos 𝑀 a enviar mensajes con el móvil y 𝑉 a jugar a videojuegos. Sabemos que: 𝑃(𝑀∪𝑉)=0,8,𝑃(𝑀∩𝑉)=0,45y𝑃(𝑉𝑐)=0,4⇒𝑃(𝑉)=0,6.

  1. Sabemos que la probabilidad de enviar mensajes o jugar a videojuegos viene dada por: 𝑃(𝑀∪𝑉)=𝑃(𝑀)+𝑃(𝑉)−𝑃(𝑀∩𝑉). Así que, despejando en la expresión anterior, la probabilidad de enviar mensajes es: 𝑃(𝑀)=𝑃(𝑀∪𝑉)−𝑃(𝑉)+𝑃(𝑀∩𝑉)=0,8−0,6+0,45=0,65. Por tanto, la probabilidad de enviar mensajes y no jugar a videojuegos es: 𝑃(𝑀−𝑉)=𝑃(𝑀)−𝑃(𝑀∩𝑉)=0,65−0,45=0,2.
  2. La probabilidad de que juegue a videojuegos sabiendo que no envía mensajes es: 𝑃(𝑉|𝑀𝑐)=𝑃(𝑉∩𝑀𝑐)𝑃(𝑀𝑐)=𝑃(𝑉)−𝑃(𝑀∩𝑉)1−𝑃(𝑀)=0,6−0,451−0,65≈0,4286.
  3. La probabilidad de que haga solo una de las dos cosas es: 𝑃(𝑀−𝑉)+𝑃(𝑉−𝑀)=𝑃(𝑀∪𝑉)−𝑃(𝑀∩𝑉)=0,8−0,45=0,35.
  4. La probabilidad de que no haga ninguna de las dos cosas es: 𝑃(𝑀𝑐∩𝑉𝑐)=1−𝑃(𝑀∪𝑉)=1−0,8=0,2.

Ejercicio 6

Un componente electrónico se produce en dos fábricas, A y B. Se exporta el 40% de los componentes producidos en A y la cuarta parte de los producidos en B, mientras que el resto es para consumo nacional. Además, el 37% de todos los componentes producidos es exportado. Si se elige un componente electrónico al azar, halle la probabilidad de que:

  1. Se haya producido en la fábrica A.
  2. Se haya producido en la fábrica A sabiendo que no es exportado.

Resolución

Llamamos 𝐴 a producir un componente en la fábrica A, 𝐵 a producir un componente en la fábrica B y 𝐸 a exportar un componente. Podemos hacer un diagrama de árbol.

𝐸
0,4←←←←←←←←←←→
𝐴
𝑝←←←←←←←←←→ 0,6←←←←←←←←←←→
𝐸𝑐
𝐸
1−𝑝←←←←←←←←←←←→ 0,25←←←←←←←←←←←→
𝐵
0,75←←←←←←←←←←←→
𝐸𝑐

También sabemos que 𝑃(𝐸) =0,37.

  1. Por el teorema de la probabilidad total, la probabilidad de exportar un componente viene dada por: 𝑃(𝐸)=𝑃(𝐴)⋅𝑃(𝐸|𝐴)+𝑃(𝐵)⋅𝑃(𝐸|𝐵)=𝑝⋅0,4+(1−𝑝)⋅0,25=0,15𝑝+0,25. Como 𝑃(𝐸) =0,37, 0,15𝑝+0,25=0,37⇔0,15𝑝=0,12⇔𝑝=0,8. Por tanto, la probabilidad de producir un componente en la fábrica A es 𝑃(𝐴) =0,8.
  2. La probabilidad de producir un componente en la fábrica A sabiendo que no es exportado es: 𝑃(𝐴|𝐸𝑐)=𝑃(𝐴∩𝐸𝑐)𝑃(𝐸𝑐)=𝑃(𝐴)⋅𝑃(𝐸𝑐|𝐴)1−𝑃(𝐸)=0,8⋅0,61−0,37≈0,7619.

Ejercicio 7

Se sabe que la vida útil en meses de una batería de coche sigue una distribución Normal de media desconocida y varianza 8 meses2. Se seleccionan al azar 100 clientes que habían comprado una de estas baterías y se les pregunta cuándo las reemplazaron, obteniéndose una media de 4 años y 2 meses.

  1. Determine, con un nivel de confianza del 94%, un intervalo de confianza para estimar la vida media de estas baterías.
  2. Manteniendo el mismo nivel de confianza, determine el tamaño muestral mínimo que debe tomarse para que el error cometido al estimar la vida media de estas baterías sea menor que 0,1 meses.

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Como el nivel de confianza es del 94%, entonces: 𝛼=1−0,94=0,06⇒1−𝛼2=1−0,062=0,97⇒𝑧𝛼/2=1,885. Además, la media muestral es de 4 años y 2 meses, es decir, de 50 meses. Por tanto, el intervalo de confianza para estimar la vida media de las baterías con un nivel de confianza del 94% es: 𝐼=(50−1,885⋅√8√100,50+1,885⋅√8√100)≈(49,4668;50,5332).
  2. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=1,885⋅√8√𝑛=1,885√8√𝑛. Si se quiere que el error máximo sea menor que 0,1, entonces: 1,885√8√𝑛=0,1⇔√𝑛=1,885√80,1⇔𝑛=1,8852⋅80,12≈2.842,58. Por tanto, el tamaño mínimo de la muestra debe ser de 2.843 personas.

Ejercicio 8

El tiempo de adaptación al uso de unas gafas progresivas depende de la persona, de la graduación de las lentes y del tipo de progresivo elegido. No obstante, se sabe que el tiempo de adaptación sigue una ley Normal de media 12,5 días y desviación típica 2,5 días.

  1. Si se toma una muestra aleatoria de 16 individuos que han comenzado a utilizar este tipo de gafas, ¿qué distribución sigue la media muestral del tiempo de adaptación? ¿Cuál es la probabilidad de que el tiempo medio de adaptación a las gafas progresivas para dicha muestra supere los 12 días?
  2. Si la muestra elegida es de tamaño 25, ¿cuál es la probabilidad de que el tiempo medio muestral de adaptación a las gafas progresivas diste de 12 días a lo sumo 1 día?

Resolución
  1. La distribución de la media muestral ――𝑋 sigue una normal 𝑁(𝜇,𝜎√𝑛) con 𝜇 =12,5, 𝜎 =2,5 y 𝑛 =16. Es decir, ――𝑋∼𝑁(12,5;0,625). La probabilidad de que el tiempo medio de adaptación para la muestra supere los 12 días es 𝑃(――𝑋>12)=𝑃(𝑍>12−12,50,625)=𝑃(𝑍>−0,8)=𝑃(𝑍≤0,8)=0,7881.
  2. Si la muestra es de tamaño 25, la distribución de la media muestral verifica ――𝑋∼𝑁(12,5;2,5√5)=𝑁(12,5;0,5). La probabilidad de que el tiempo medio de adaptación para la muestra diste de 12 días a lo sumo 1 es 𝑃(11≤――𝑋≤13)=𝑃(11−12,50,5≤𝑍≤13−12,50,5)=𝑃(−3≤𝑍≤1)=𝑃(𝑍≤1)−𝑃(𝑍≤−3)==𝑃(𝑍≤1)−(1−𝑃(𝑍≤3))≈0,84.