Icono Matemáticas de Selectividad

Buscar GitHub

📋 Julio de 2024

Ejercicio 1

Dada la matriz 𝐴=⎛⎜ ⎜ ⎜⎝1200−12−201⎞⎟ ⎟ ⎟⎠, resuelva la ecuación 𝐴2𝑋 +𝐴4 =𝐴.

Resolución

En primer lugar, calculamos el determinante de la matriz 𝐴. |𝐴|=∣1200−12−201∣=−9. Así que 𝐴 es invertible con det(𝐴) = −9.

Despejamos la ecuación matricial. 𝐴2𝑋+𝐴4=𝐴⇔𝐴2𝑋=𝐴−𝐴4⇔𝑋=𝐴−2(𝐴−𝐴4)=𝐴−1−𝐴2.

Por un lado, calculamos 𝐴2=⎛⎜ ⎜ ⎜⎝1200−12−201⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝1200−12−201⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝104−410−4−41⎞⎟ ⎟ ⎟⎠.

Por otro lado, para hallar la inversa de 𝐴 calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝−1−4−2−21−44−2−1⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=−19⎛⎜ ⎜ ⎜⎝−1−24−41−2−2−4−1⎞⎟ ⎟ ⎟⎠=19⎛⎜ ⎜ ⎜⎝12−44−12241⎞⎟ ⎟ ⎟⎠.

Por último, calculamos la matriz 𝑋 operando. 𝑋=𝐴−1−𝐴2=19⎛⎜ ⎜ ⎜⎝12−44−12241⎞⎟ ⎟ ⎟⎠−⎛⎜ ⎜ ⎜⎝104−410−4−41⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜ ⎜⎝−8929−409409−10929389409−89⎞⎟ ⎟ ⎟ ⎟ ⎟⎠=29⎛⎜ ⎜ ⎜⎝−41−2020−511920−4⎞⎟ ⎟ ⎟⎠.

Ejercicio 2

Una empresa tiene un presupuesto de 78.000€ para promocionar un producto y quiere contratar la emisión de anuncios por radio y televisión. El coste de emisión de un anuncio de radio es de 2.400€ y de un anuncio de televisión de 3.600€. La empresa quiere que la diferencia entre el número de anuncios emitidos de cada tipo no sea mayor que 10 y que se emitan un mínimo de 10 anuncios en total. Si la emisión de un anuncio de radio llega a 34.000 personas y de un anuncio de televisión a 72.000 personas, ¿cuántas emisiones de cada tipo debe contratar para que la audiencia sea la mayor posible? ¿A cuánto ascendería dicha audiencia?

Resolución

Llamamos 𝑥 al número de emisiones de anuncios por radio e 𝑦 al de anuncios por televisión. Las restricciones del problema son: ⎧{ { {⎨{ { {⎩2.400𝑥+3.600𝑦≤78.000,𝑥−𝑦≤10,𝑦−𝑥≤10,𝑥+𝑦≥10⇔⎧{ { {⎨{ { {⎩6𝑥+9𝑦≤195,𝑥−𝑦≤10,𝑦−𝑥≤10,𝑥+𝑦≥10. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=34.000𝑥+72.000𝑦.

Representamos la región. 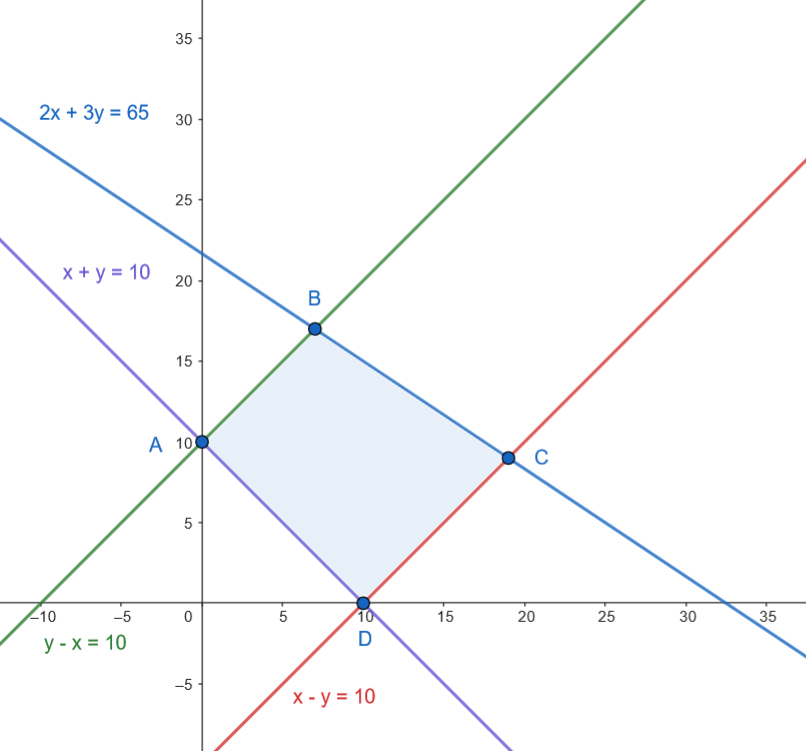Figura Los vértices son: 𝐴(0,10),𝐵(7,17),𝐶(19,9)y𝐷(10,0).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(0,10)=720.000,𝐹(𝐵)=𝐹(7,17)=1.462.000,𝐹(𝐶)=𝐹(19,9)=1.294.000,𝐹(𝐷)=𝐹(10,0)=340.000. Por tanto, el valor máximo de audiencia se alcanza contratando 7 emisiones de radio y 17 de televisión, con una audiencia de 1.462.000 personas.

Ejercicio 3

Dada la función 𝑓(𝑥)=2𝑥−62−𝑥.

  1. Estudie la continuidad y derivabilidad de dicha función. Calcule sus asíntotas.
  2. Estudie los intervalos de crecimiento y decrecimiento, así como la existencia de extremos relativos.
  3. Halle los puntos de corte con los ejes de coordenadas y represente gráficamente la función.

Resolución
  1. En primer lugar, observamos que Dom⁡(𝑓) =ℝ ∖{2}. La función 𝑓 es racional, así que es continua y derivable en todo su dominio. Estudiamos las asíntotas.
    • El denominador se anula en 𝑥 =2 y observamos que lím𝑥→2−⁡𝑓(𝑥)=lím𝑥→2−⁡2𝑥−62−𝑥=−∞,lím𝑥→2+⁡𝑓(𝑥)=lím𝑥→2+⁡2𝑥−62−𝑥=+∞. Por tanto, la recta 𝑥 =2 es una asíntota vertical.
    • Veamos si tiene una asíntota horizontal. lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡2𝑥−62−𝑥=−2. Por tanto, la recta 𝑦 = −2 es una asíntota horizontal.
  2. En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=2(2−𝑥)+2𝑥−6(2−𝑥)2=−2(2−𝑥)2. Observamos que 𝑓′(𝑥) <0 para 𝑥 ≠2, así que 𝑓 es decreciente en todo su dominio y no tiene extremos.
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑓(𝑥)=0⇔2𝑥−62−𝑥=0⇔2𝑥−6=0⇔𝑥=3. Luego el único punto de corte con el eje 𝑋 es (3,0).
    • Hallamos ahora el punto de corte con el eje 𝑌. 𝑓(0)=−62=−3. Así que el punto de corte con el eje 𝑌 es (0, −3).
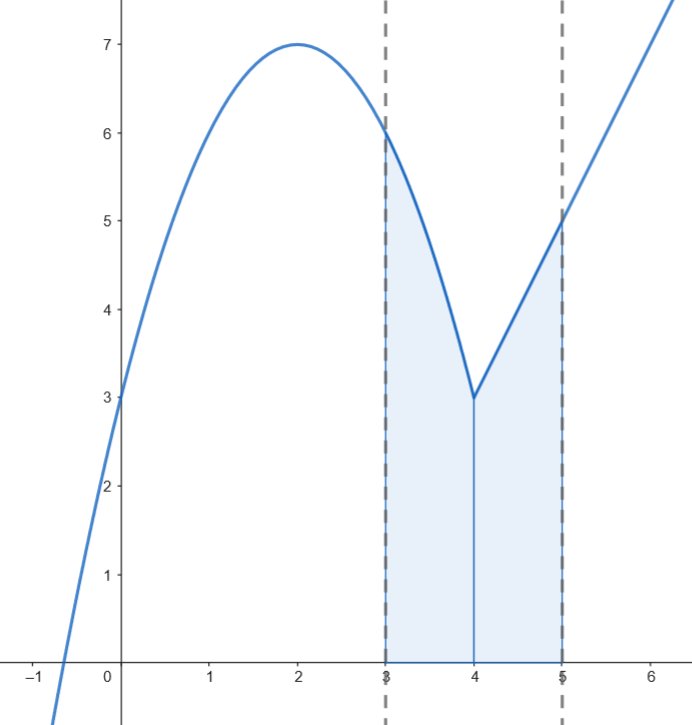    Representamos gráficamente la función usando los puntos de corte y la información de los apartados anteriores. Figura

Ejercicio 4

Se considera la función 𝑓(𝑥)={−𝑥2+4𝑥+3,si 𝑥<4,2𝑥−5,si 𝑥≥4.

  1. Estudie su continuidad y derivabilidad.
  2. Estudie su monotonía y calcule sus extremos relativos.
  3. Represente la región del plano limitada por la gráfica de 𝑓, las rectas 𝑥 =3, 𝑥 =5 y el eje de abscisas. Calcule su área.

Resolución
  1. Estudiamos la continuidad y la derivabilidad de 𝑓.
    • Si 𝑥 ≠4, 𝑓 es continua y derivable con 𝑓′(𝑥)={−2𝑥+4,si 𝑥<4,2,si 𝑥>4.
    • Estudiamos la continuidad para el punto de ruptura 𝑥 =4. lím𝑥→4−⁡𝑓(𝑥)=lím𝑥→4−⁡(−𝑥2+4𝑥+3)=3,lím𝑥→4+⁡𝑓(𝑥)=lím𝑥→4+⁡(2𝑥−5)=3,𝑓(4)=3. Observamos que lím𝑥→4−⁡𝑓(𝑥)=lím𝑥→4+⁡𝑓(𝑥)=𝑓(4). Así que 𝑓 es continua en 𝑥 =4. Pasamos a estudiar la derivabilidad. 𝑓′−(4)=lím𝑥→4−⁡𝑓′(𝑥)=lím𝑥→4−⁡(−2𝑥+4)=−4,𝑓′+(4)=lím𝑥→4+⁡𝑓′(𝑥)=lím𝑥→4+⁡2=2. Así que 𝑓 no es derivable en 𝑥 =4.
    Por tanto, 𝑓 es continua en ℝ y derivable en ℝ ∖{4}.
  2. Para hallar los puntos críticos, igualamos las dos ramas de la derivada a cero.
    • Si 𝑥 <4, 𝑓′(𝑥)=0⇔−2𝑥+4=0⇔𝑥=2.
    • Si 𝑥 >4, 𝑓′(𝑥)=2≠0.
    Así que el único punto crítico es 𝑥 =2. También consideramos 𝑥 =4 por no ser derivable. Estudiamos el signo de la derivada.
    ( −∞,2) (2,4) (4, +∞)
    signo de 𝑓′ + − +
    monotonía de 𝑓 → → →
    Por tanto, 𝑓 es creciente en ( −∞,2) ∪(4, +∞) y decreciente en (2,4). Además, el punto (2,7) es un máximo relativo y el punto (4,3) es un mínimo relativo.
  3. Representamos el recinto limitado por la gráfica de 𝑓, el eje 𝑋 y las rectas 𝑥 =3 y 𝑥 =5. Observamos que la parábola tiene vértice (2,7). Figura Calculamos el área. ∫43(−𝑥2+4𝑥+3)𝑑𝑥+∫54(2𝑥−5)𝑑𝑥=[−13𝑥3+2𝑥2+3𝑥]43+[𝑥2−5𝑥]54=−643+32+12−(−9+18+9)+25−25−(16−20)=263𝑢2.

Ejercicio 5

El 7% de los habitantes de una ciudad no tienen ni coche ni moto. De entre los que tienen coche el 36% tienen moto y de entre los que no tienen coche el 28% no tienen moto. Se elige al azar un habitante de esa ciudad.

  1. Calcule la probabilidad de que solo tenga uno de los dos vehículos.
  2. Calcule la probabilidad de que al menos tenga uno de los dos vehículos.
  3. Si tiene coche, ¿cuál es la probabilidad de que no tenga moto?
  4. ¿Son independientes los sucesos "tener coche" y "no tener moto"? ¿Son incompatibles?

Resolución

Llamamos 𝐶 a tener coche y 𝑀 a tener moto. Sabemos que 𝑃(𝑀𝑐∩𝐶𝑐)=0,07,𝑃(𝑀|𝐶)=0,36y𝑃(𝑀𝑐|𝐶𝑐)=0,28. En primer lugar, podemos hallar algunas probabilidades a partir de los datos. Calculamos la probabilidad de la unión. 𝑃(𝑀∪𝐶)=1−𝑃((𝑀∪𝐶)𝑐)=1−𝑃(𝑀𝑐∩𝐶𝑐)=1−0,07=0,93. Hallamos también la probabilidad de tener coche. 𝑃(𝑀𝑐|𝐶𝑐)=𝑃(𝑀𝑐∩𝐶𝑐)𝑃(𝐶𝑐)=𝑃(𝑀𝑐∩𝐶𝑐)1−𝑃(𝐶)⇒⇒𝑃(𝐶)=1−𝑃(𝑀𝑐∩𝐶𝑐)𝑃(𝑀𝑐|𝐶𝑐)=1−0,070,28=0,75. Por último, calculamos la probabilidad de la intersección. 𝑃(𝑀∩𝐶)=𝑃(𝐶)⋅𝑃(𝑀|𝐶)=0,75⋅0,36=0,27.

  1. La probabilidad de que solo tenga uno de los dos vehículos es 𝑃(𝑀∪𝐶)−𝑃(𝑀∩𝐶)=0,93−0,27=0,66.
  2. La probabilidad de que al menos tenga uno de los dos vehículos es 𝑃(𝑀∪𝐶)=0,93.
  3. La probabilidad de que no tenga moto sabiendo que tiene coche es 𝑃(𝑀𝑐|𝐶)=1−𝑃(𝑀|𝐶)=1−0,36=0,64.
  4. En primer lugar, calculamos la probabilidad de que tenga moto usando la probabilidad de la unión. 𝑃(𝑀∪𝐶)=𝑃(𝑀)+𝑃(𝐶)−𝑃(𝑀∩𝐶)⇒⇒𝑃(𝑀)=𝑃(𝑀∪𝐶)+𝑃(𝑀∩𝐶)−𝑃(𝐶)=0,93+0,27−0,75=0,45. Como 𝑃(𝑀) ≠𝑃(𝑀|𝐶), los sucesos 𝑀 y 𝐶 no son independientes. Por otro lado, como 𝑃(𝑀 ∩𝐶) >0, los sucesos no son incompatibles.

Ejercicio 6

Se ha realizado un estudio a personas que están teletrabajando actualmente. De estos, el 72% trabajan por cuenta ajena con contrato indefinido, el 11% lo hacen por cuenta ajena con contrato temporal y el resto trabajan por cuenta propia. El 87% de los que tienen contrato indefinido y el 86% de los que trabajan por cuenta propia piensan que el teletrabajo mejora la conciliación familiar. Además, este estudio ha revelado que el 12,51% de los trabajadores opinan que el teletrabajo no mejora la conciliación familiar. Seleccionado un teletrabajador al azar, determine la probabilidad de que:

  1. Opine que el teletrabajo sí mejora la conciliación familiar sabiendo que tiene un contrato temporal.
  2. No esté trabajando por cuenta propia sabiendo que opina que el teletrabajo mejora la conciliación familiar.

Resolución

Llamamos 𝐼 a trabajar con contrato indefinido, 𝑇 con contrato temporal, 𝐴 por cuenta propia y 𝐹 a pensar que el teletrabajo mejora la conciliación familiar. Podemos hacer un diagrama de árbol.

𝐹
0,87←←←←←←←←←←←→
𝐼
0,72←←←←←←←←←←←→ 0,13←←←←←←←←←←←→
𝐹𝑐
𝐹
𝑝←←←←←←←←←→
0,11←←←←←←←←←←←→ 𝑇
1−𝑝←←←←←←←←←←←→
𝐹𝑐
𝐹
0,17←←←←←←←←←←←→ 0,86←←←←←←←←←←←→
𝐴
0,14←←←←←←←←←←←→
𝐹𝑐

También sabemos que: 𝑃(𝐹𝑐)=0,1251⇒𝑃(𝐹)=0,8749.

  1. Por el teorema de la probabilidad total, la probabilidad de que opine que el teletrabajo mejora la conciliación familiar viene dada por: 𝑃(𝐹)=𝑃(𝐼)⋅𝑃(𝐹|𝐼)+𝑃(𝑇)⋅𝑃(𝐹|𝑇)+𝑃(𝐴)⋅𝑃(𝐹|𝐴)==0,72⋅0,87+0,11⋅𝑝+0,17⋅0,86=0,11𝑝+0,7726. Como 𝑃(𝐹) =0,8749, 0,11𝑝+0,7726=0,8749⇔0,11𝑝=0,1023⇔𝑝=0,93. Por tanto, la probabilidad de que opine que el teletrabajo mejora la conciliación familiar sabiendo que tiene un contrato temporal es 𝑃(𝐹|𝑇) =0,93.
  2. La probabilidad de que no esté trabajando por cuenta propia sabiendo que opina que el teletrabajo mejora la conciliación familiar es: 𝑃(𝐴𝑐|𝐹)=1−𝑃(𝐴|𝐹)=1−𝑃(𝐴∩𝐹)𝑃(𝐹)=1−0,17⋅0,860,8749≈0,8329.

Ejercicio 7

La altura de un cierto tipo de plantas de maíz sigue una distribución Normal de media 145 cm y desviación típica 22 cm.

  1. ¿Qué porcentaje de plantas tiene una altura comprendida entre 135 cm y 155 cm?
  2. ¿Qué altura, como mínimo, debe tener una planta para estar entre el 50% de las más altas?
  3. Se selecciona una muestra aleatoria de 16 plantas. Halle la probabilidad de que la altura media de las plantas de esta muestra esté comprendida entre 140 cm y 151 cm.

Resolución

Llamamos 𝑋 ∼𝑁(145,22) a la distribución de la altura de las plantas.

  1. Calculamos la probabilidad de que la altura esté entre 135 cm y 155 cm. 𝑃(135≤𝑋≤155)=𝑃(135−14522≤𝑍≤155−14522)=𝑃(−511≤𝑍≤511)==𝑃(𝑍≤511)−𝑃(𝑍≤−511)=𝑃(𝑍≤511)−(1−𝑃(𝑍≤511))=2𝑃(𝑍≤511)−1≈0,3472. Así que un 34,72% de las plantas tiene una altura comprendida entre 135 cm y 155 cm.
  2. Como la altura de las plantas sigue una distribución normal, el centro de la distribución se encuentra en la media. Por tanto, una planta debe tener al menos una altura de 145 cm para estar entre el 50% de las más altas.
  3. La distribución de las medias muestrales ――𝑋 sigue una normal 𝑁(𝜇,𝜎√𝑛) con 𝜇 =145, 𝜎 =22 y 𝑛 =16. Es decir, ――𝑋 ∼𝑁(145; 5,5). Calculamos la probabilidad. 𝑃(140≤――𝑋≤151)=𝑃(140−1455,5≤𝑍≤151−1455,5)=𝑃(−1011≤𝑍≤1211)==𝑃(𝑍≤1211)−𝑃(𝑍≤−1011)=𝑃(𝑍≤1211)−(1−𝑃(𝑍≤1011))≈0,6807.

Ejercicio 8

Se desea estimar la proporción de personas que viajan en tren con su mascota. Para ello, se selecciona una muestra aleatoria de 300 viajeros, obteniéndose que 12 de ellos viajan con su mascota.

  1. Obtenga un intervalo, con un nivel de confianza del 97%, para estimar la proporción de personas que viajan en tren con su mascota.
  2. Manteniendo la misma proporción muestral y con un nivel de confianza del 95%, ¿cuántas personas que viajan en tren deberán seleccionarse aleatoriamente como mínimo para que la proporción muestral difiera de la proporción poblacional a lo sumo en un 2%?

Resolución
  1. Como 12 personas de 𝑛 =300 viajan con su mascota, la proporción muestral es: 𝑝=12300=0,04. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar la proporción de personas que viajan con su mascota con un nivel de confianza del 97% es: 𝐼=(0,04−2,17⋅√0,04⋅(1−0,04)300,0,04+2,17⋅√0,04⋅(1−0,04)300)≈(0,0154;0,0646).
  2. Si el nivel de confianza es del 95%, entonces: 𝛼=1−0,95=0,05⇒1−𝛼2=1−0,052=0,975⇒𝑧𝛼/2=1,96. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=1,96⋅√0,04⋅(1−0,04)𝑛=1,96⋅√0,0384𝑛. Si se quiere el error no sea mayor que 0,02, entonces: 1,96⋅√0,0384𝑛=0,02⇔√0,0384𝑛=0,021,96⇔0,0384𝑛=0,0221,962⇔𝑛=0,0384⋅1,9620,022=368,7936. Por tanto, el número mínimo de viajeros de la muestra debe ser 369.