Icono Matemáticas de Selectividad

Buscar GitHub

📋 Junio de 2023

Ejercicio 1

Sean la función 𝐹(𝑥,𝑦) =5𝑥 −3𝑦 y la región del plano 𝑅 definida mediante las inecuaciones 2𝑥−3𝑦≤1,4𝑥+𝑦≤9,𝑥+𝑦≤5,9𝑥−𝑦≥0,𝑦≥0.

  1. Dibuje la región 𝑅 y calcule sus vértices.
  2. Indique razonadamente si los puntos 𝐴(2,2) y 𝐵(1;3,5) pertenecen a la región 𝑅.
  3. Obtenga los puntos de la región 𝑅 donde 𝐹 alcanza el máximo y el mínimo y calcula sus correspondientes valores.

Resolución
  1. Dibujamos la región 𝑅. 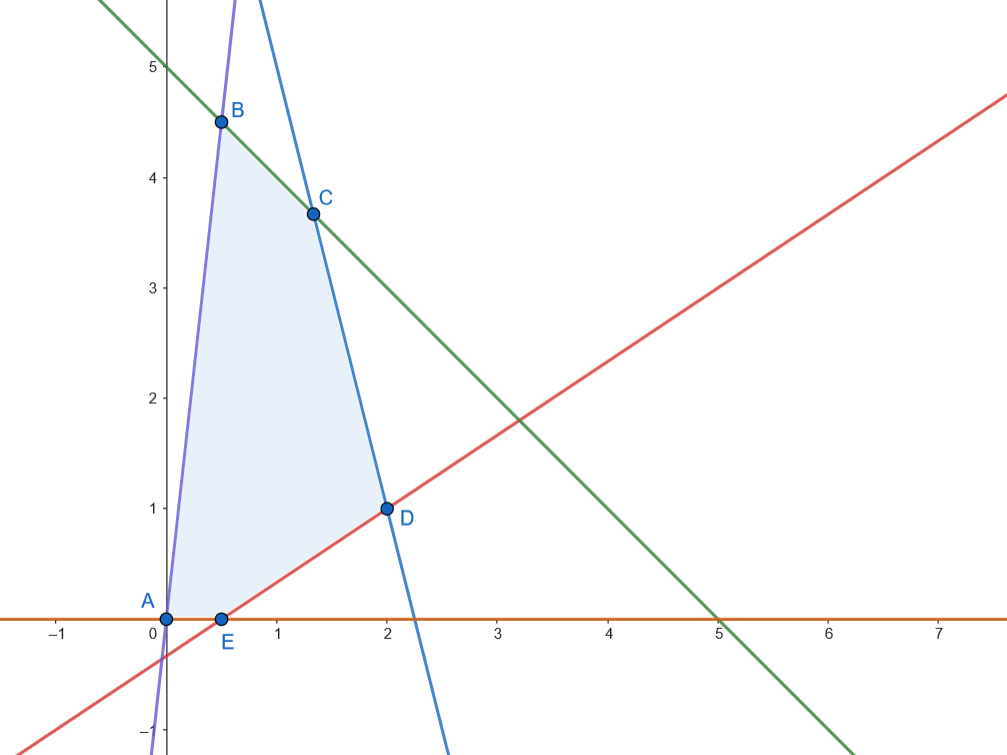Figura Los vértices son 𝐴(0,0),𝐵(0,5;4,5),𝐶(43,113),𝐷(2,1)y𝐸(0,5;0).
  2. Un punto pertenece a la región 𝑅 si verifica todas las inecuaciones que la definen.
    • Veamos si el punto (2,2) pertenece a 𝑅. 2⋅2−3⋅2=−2≤1,4⋅2+2=10≰9. Como no verifica la segunda inecuación, no pertenece a la región.
    • Veamos si el punto (1;3,5) pertenece a 𝑅. 2⋅1−3⋅3,5=−8,5≤1,4⋅1+3,5=7.5≤9,1+3,5=4,5≤5,9⋅1−3,5=5,5≥0,3,5≥0. Como verifica todas las inecuaciones, pertenece a la región.
  3. Para hallar los valores máximos y mínimos de la función 𝐹, la evaluamos en los vértices. 𝐹(𝐴)=𝐹(0,0)=0,𝐹(𝐵)=𝐹(0,5;4,5)=−11,𝐹(𝐶)=𝐹(43,113)=−133≈−4,33,𝐹(𝐷)=𝐹(2,1)=7,𝐹(𝐸)=𝐹(0,5;0)=2,5. Por tanto, el máximo se alcanza en el punto 𝐷(2,1) y el valor de la función es 7, mientras que el mínimo se alcanza en el punto 𝐶(43,113) y el valor es −133.

Ejercicio 2

Dadas las matrices 𝐴=⎛⎜ ⎜ ⎜⎝𝑎100𝑎2011⎞⎟ ⎟ ⎟⎠,𝐵=(2−1𝑎−1)y𝐶=⎛⎜ ⎜ ⎜⎝2−11−120⎞⎟ ⎟ ⎟⎠.

  1. Calcule los valores del parámetro 𝑎 para los que tanto 𝐴 como 𝐵 admitan inversa.
  2. Para 𝑎 =1, halle una matriz 𝑋 que satisfaga 𝐴𝑋𝐵 =𝐶.

Resolución
  1. Calculamos en primer lugar los determinantes de las matrices 𝐴 y 𝐵. |𝐴|=∣𝑎100𝑎2011∣=𝑎2−2𝑎,|𝐵|=∣2−1𝑎−1∣=−2+𝑎. La inversa de una matriz existe si y solo si su determinante es no nulo. |𝐴|=0⇔𝑎2−2𝑎=0⇔𝑎(𝑎−2)=0⇔{𝑎=0,𝑎−2=0⇔𝑎=2,|𝐵|=0⇔−2+𝑎=0⇔𝑎=2. Así que la matriz 𝐴 tiene inversa si 𝑎 ≠0 y 𝑎 ≠2, mientras que 𝐵 tiene inversa si 𝑎 ≠2. Por tanto, 𝐴 y 𝐵 admiten inversa si 𝑎 ≠0 y 𝑎 ≠2.
  2. Si 𝑎 =1, por el apartado anterior 𝐴 y 𝐵 son invertibles con det(𝐴) = −1 y det(𝐵) = −1. Resolvemos la ecuación matricial. 𝐴𝑋𝐵=𝐶⇔𝑋=𝐴−1𝐶𝐵−1. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝−100−11−12−21⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=⎛⎜ ⎜ ⎜⎝11−20−1201−1⎞⎟ ⎟ ⎟⎠. Repetimos el mismo procedimiento para hallar la inversa de 𝐵. Calculamos su matriz adjunta: Adj⁡(𝐵)=(−1−112). Calculamos su inversa como 𝐵−1=1|𝐵|Adj⁡(𝐵)𝑡=(1−11−2). Por último, calculamos la matriz 𝑋 operando. 𝑋=𝐴−1𝐶𝐵−1=⎛⎜ ⎜ ⎜⎝11−20−1201−1⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝2−11−120⎞⎟ ⎟ ⎟⎠(1−11−2)=⎛⎜ ⎜ ⎜⎝−1−231−1−1⎞⎟ ⎟ ⎟⎠(1−11−2)=⎛⎜ ⎜ ⎜⎝−354−5−23⎞⎟ ⎟ ⎟⎠.

Ejercicio 3

Se considera la función 𝑓(𝑥) =𝑥3 −3𝑥2 +2𝑥.

  1. Halle los puntos de corte con los ejes, los intervalos de crecimiento y decrecimiento, los extremos relativos de 𝑓 y su curvatura.
  2. Represente gráficamente la función 𝑓.
  3. Calcule el área del recinto acotado, limitado por la gráfica de 𝑓 y el eje de abscisas.

Resolución
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑓(𝑥)=0⇔𝑥3−3𝑥2+2𝑥=0⇔𝑥(𝑥2−3𝑥+2)=0⇔⎧{ {⎨{ {⎩𝑥=0,𝑥2−3𝑥+2=0⇔{𝑥=1,𝑥=2. Luego los puntos de corte con el eje 𝑋 son (0,0), (1,0) y (2,0). Observamos que (0,0) es por tanto el punto de corte con el eje 𝑌.
    • Estudiamos la monotonía y los extremos. En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=3𝑥2−6𝑥+2. Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔3𝑥2−6𝑥+2=0⇔𝑥=3±√33=1±√33. Estudiemos el signo de la derivada.
      (−∞,1−√33) (1−√33,1+√33) (1+√33,+∞)
      signo de 𝑓′ + − +
      monotonía de 𝑓 → → →
      Por tanto, 𝑓 es creciente en (−∞,1−√33) ∪(1+√33,+∞) y es decreciente en (1−√33,1+√33). Además, tiene un máximo relativo en 𝑥 =1 −√33 y un mínimo relativo en 1 +√33. Es decir, el punto (0,42; 0,38) es un máximo relativo y el punto (1,58; −0,38) es un mínimo relativo.
    • Estudiamos la curvatura. Para ello, calculamos la segunda derivada de 𝑓. 𝑓″(𝑥)=6𝑥−6. Para hallar los candidatos a puntos de inflexión, igualamos la segunda derivada a cero. 𝑓″(𝑥)=0⇔6𝑥−6=0⇔𝑥=1. Estudiemos el signo de la segunda derivada.
      ( −∞,1) (1, +∞)
      signo de 𝑓″ − +
      curvatura de 𝑓 ⌢ ⌣
      Por tanto, 𝑓 es convexa en (1, +∞) y es cóncava en ( −∞,1). Además, tiene un punto de inflexión en 𝑥 =1, es decir, el punto (1,0).
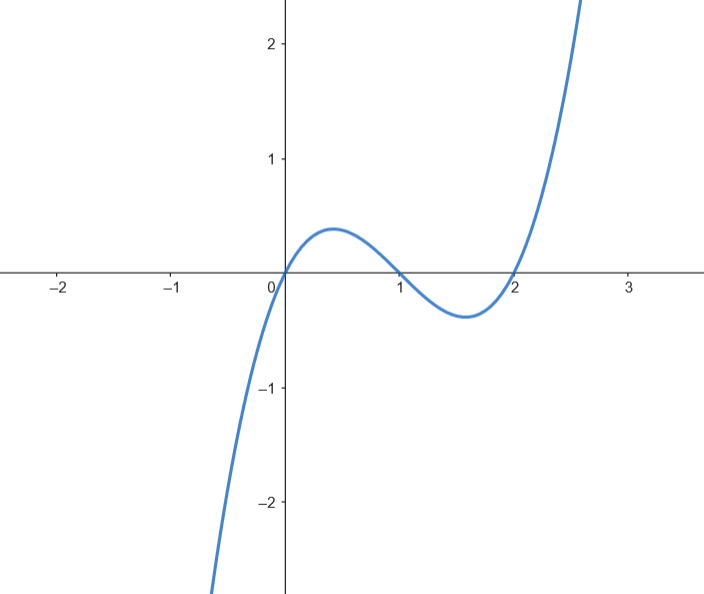
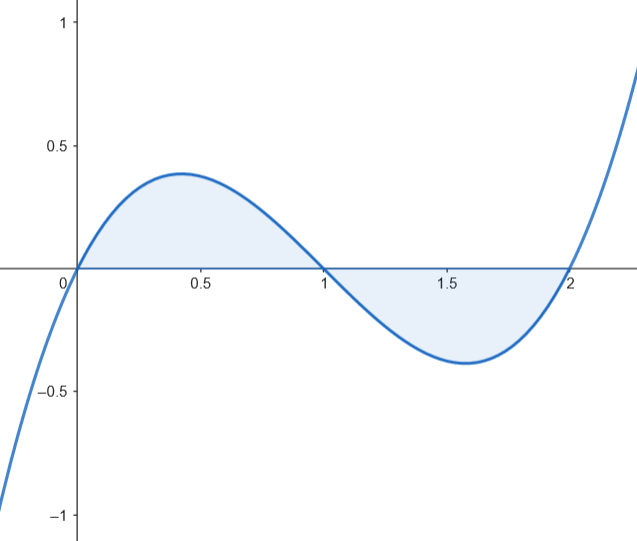  2. Representamos gráficamente la función usando la información del apartado anterior. Figura
  3. Podemos representar el recinto acotado limitado por la gráfica de 𝑓 y el eje 𝑋. Figura Calculamos el área. ∫10𝑓(𝑥)𝑑𝑥+∫21−𝑓(𝑥)𝑑𝑥=∫10(𝑥3−3𝑥2+2𝑥)𝑑𝑥+∫21−(𝑥3−3𝑥2+2𝑥)𝑑𝑥==[14𝑥4−𝑥3+𝑥2]10−[14𝑥4−𝑥3+𝑥2]21=14−(−14)=12𝑢2.

Ejercicio 4

Se desea analizar el valor de las acciones de una empresa en un día. La función 𝑣(𝑡) nos indica el valor, en euros, de cada acción de la empresa en función del tiempo 𝑡, medido en horas, a partir de la hora de apertura del mercado. De la función 𝑣(𝑡) se conoce que su variación instantánea es 𝑣′(𝑡)=𝑡2−5𝑡+6,𝑡∈[0,6].

  1. Determine los intervalos de crecimiento y decrecimiento de la función 𝑣.
  2. Si en el momento de la apertura del mercado se conoce que 𝑣(0) =10, halle la función 𝑣.
  3. Si un inversor compró 3.000 de estas acciones en el instante 𝑡 =2 y posteriormente las vendió en el instante 𝑡 =4, indique a cuánto ascendió la ganancia o la pérdida que obtuvo el inversor con esta gestión.
  4. ¿En qué momentos debería haber realizado este inversor las gestiones de compra y de venta para que la ganancia hubiese sido máxima? Justifique su respuesta.

Resolución
  1. Para hallar los puntos críticos, igualamos la derivada de 𝑣 a cero. 𝑣′(𝑡)=0⇔𝑡2−5𝑡+6=0⇔{𝑡=2,𝑡=3. Así que los puntos críticos se encuentran en 𝑡 =2 y 𝑡 =3. Estudiemos el signo de la derivada.
    (0,2) (2,3) (3,6)
    signo de 𝑣′ + − +
    monotonía de 𝑣 → → →
    Por tanto, 𝑣 es creciente en (0,2) ∪(3,6) y es decreciente en (2,3).
  2. Como 𝑣′ es la derivada de 𝑣, entonces 𝑣(𝑡)=∫𝑣′(𝑡)𝑑𝑡=∫(𝑡2−5𝑡+6)𝑑𝑡=13𝑡3−52𝑡2+6𝑡+𝐶. Además, 𝑣(0)=10⇔𝐶=10. Por tanto, 𝑣(𝑡)=13𝑡3−52𝑡2+6𝑡+10.
  3. Calculamos los valores de cada acción de la empresa en los instantes 𝑡 =2 y 𝑡 =4. 𝑣(2)=83−10+12+10=443,𝑣(4)=643−40+24+10=463. Así que el incremento de valor de cada acción es de 𝑣(4)−𝑣(2)=463−443=23. Por tanto, la ganancia obtenida por la compra de 3.000 acciones es de 3.000 ⋅23 =2.000€.
  4. Por el primer apartado, sabemos que la función 𝑣 tiene máximos relativos en 𝑡 =2 y 𝑡 =6 y tiene mínimos relativos en 𝑡 =0 y 𝑡 =3. Observamos que 𝑣(0)=10,𝑣(2)=443≈14,67,𝑣(3)=292=14,5,𝑣(6)=28. Así que el máximo absoluto se encuentra en 𝑡 =6 y el mínimo absoluto en 𝑡 =0. Por tanto, el mejor momento para comprar acciones es a la apertura del mercado (el instante 𝑡 =0) y el mejor momento para venderlas es a las seis horas.

Ejercicio 5

Disponemos de una moneda trucada en la que la probabilidad de obtener cara, al lanzarla, es el doble de la de obtener cruz.

  1. Halle la probabilidad de que, al lanzar la moneda, se obtenga cara.
  2. Halle la probabilidad de que, al lanzar dos veces la moneda, se obtenga una cara y una cruz sin importar el orden.
  3. Halle la probabilidad de que, al lanzar dos veces la moneda, se obtenga al menos una cara.
  4. Si al lanzar la moneda dos veces observamos que ha salido al menos una cara, halle la probabilidad de que se obtengan dos caras.

Resolución
  1. Llamamos 𝐶 a obtener cara y 𝑋 a obtener cruz. Como son sucesos complementarios y la probabilidad de obtener cara es el doble de la probabilidad de obtener cruz, entonces: {𝑃(𝐶)+𝑃(𝑋)=1,𝑃(𝐶)=2𝑃(𝑋) Podemos resolver este sistema por reducción. Si restamos las dos ecuaciones, obtenemos que: 𝑃(𝑋)=1−2𝑃(𝑋)⇔3𝑃(𝑋)=1⇔𝑃(𝑋)=13. Sustituyendo, 𝑃(𝐶)=2𝑃(𝑋)𝑃(𝑋)=1/3←←←←←←←←←←←←→𝑃(𝐶)=23. Por tanto, 𝑃(𝐶) =23 y 𝑃(𝑋) =13.
  2. Podemos hacer un diagrama de árbol.
    𝐶2
    2/3←←←←←←←←←←←→
    𝐶1
    2/3←←←←←←←←←←←→ 1/3←←←←←←←←←←←→
    𝑋2
    𝐶2
    1/3←←←←←←←←←←←→ 2/3←←←←←←←←←←←→
    𝑋1
    1/3←←←←←←←←←←←→
    𝑋2
    La probabilidad de obtener una cara y una cruz es: 𝑃(𝐶1∩𝑋2)+𝑃(𝑋1∩𝐶2)=𝑃(𝐶1)⋅𝑃(𝑋2|𝐶1)+𝑃(𝑋1)⋅𝑃(𝐶2|𝑋1)=23⋅13+13⋅23=49.
  3. La probabilidad de obtener al menos una cara es: 𝑃(𝐶1∪𝐶2)=𝑃(𝐶1∩𝐶2)+𝑃(𝐶1∩𝑋2)+𝑃(𝑋1∩𝐶2)==𝑃(𝐶1)⋅𝑃(𝐶2|𝐶1)+𝑃(𝐶1)⋅𝑃(𝑋1|𝐶1)+𝑃(𝑋1)⋅𝑃(𝐶2|𝑋1)=23⋅23+23⋅13+13⋅23=89.
  4. La probabilidad de obtener dos caras sabiendo que ha salido una cara es: 𝑃(𝐶1∩𝐶2|𝐶1∪𝐶2)=𝑃(𝐶1∩𝐶2)𝑃(𝐶1∪𝐶2)=𝑃(𝐶1)⋅𝑃(𝐶2|𝐶1)𝑃(𝐶1∪𝐶2)=23⋅2389=12.

Ejercicio 6

En una base de datos de correos electrónicos se ha observado que el 20% de los correos recibidos son spam. Además, se ha observado que la palabra "lottery" ha aparecido en el 40% de los correos que son spam y en el 0,6% de los correos que no lo son.

  1. Halle la probabilidad de que en un correo elegido al azar en el que aparezca la palabra "lottery" sea spam.
  2. Halle la probabilidad de que un correo elegido al azar en el que no aparezca la palabra "lottery" no sea spam.
  3. Si un correo se etiqueta como spam si aparece la palabra "lottery" y como no spam si esta palabra no aparece, calcule la probabilidad de que un correo se etiquete incorrectamente.

Resolución

Llamamos 𝑆 a recibir un correo de spam y 𝐿 a recibir un correo con la palabra "lottery". Podemos hacer un diagrama de árbol.

𝐿
0,4←←←←←←←←←←→
𝑆
0,2←←←←←←←←←←→ 0,6←←←←←←←←←←→
𝐿𝑐
𝐿
0,8←←←←←←←←←←→ 0,006←←←←←←←←←←←←→
𝑆𝑐
0,994←←←←←←←←←←←←→
𝐿𝑐
  1. Por el teorema de la probabilidad total, la probabilidad de recibir un correo con la palabra "lottery" es: 𝑃(𝐿)=𝑃(𝐿∩𝑆)+𝑃(𝐿∩𝑆𝑐)=𝑃(𝑆)⋅𝑃(𝐿|𝑆)+𝑃(𝑆𝑐)⋅𝑃(𝐿|𝑆𝑐)=0,2⋅0,4+0,8⋅0,006=0,0848. Por tanto, la probabilidad de que un correo con la palabra "lotery" sea de spam es: 𝑃(𝑆|𝐿)=𝑃(𝑆∩𝐿)𝑃(𝐿)=𝑃(𝑆)⋅𝑃(𝐿|𝑆)𝑃(𝐿)=0,2⋅0,40,0848≈0,9434.
  2. La probabilidad de que un correo sin la palabra "lotery" no sea de spam es: 𝑃(𝑆𝑐|𝐿𝑐)=𝑃(𝑆𝑐∩𝐿𝑐)𝑃(𝐿𝑐)=𝑃(𝑆𝑐)⋅𝑃(𝐿𝑐|𝑆𝑐)1−𝑃(𝐿)=0,8⋅0,9941−0,0848≈0,8689.
  3. La probabilidad de que un correo se etiquete incorrectamente es: 𝑃(𝑆∩𝐿𝑐)+𝑃(𝑆𝑐∩𝐿)=𝑃(𝑆)⋅𝑃(𝐿𝑐|𝑆)+𝑃(𝑆𝑐)⋅𝑃(𝐿|𝑆𝑐)=0,2⋅0,6+0,8⋅0,006=0,1248.

Ejercicio 7

  1. Una población está dividida en cuatro estratos de 250, 300, 400 y 350 individuos. Realizado un muestreo aleatorio estratificado con afijación proporcional se han seleccionado 20 individuos del primer estrato. Determine el tamaño de la población, el tamaño de la muestra y el número de individuos seleccionados de los tres restantes estratos.
  2. En un centro de enseñanza la calificación media de los estudiantes fue de 6,4 puntos con una desviación típica de 0,7 puntos. Se seleccionó aleatoriamente una muestra de 49 estudiantes.
    1. Indique la distribución que sigue la media de las muestras de tamaño 49.
    2. Calcule la probabilidad de que la media de las calificaciones de los estudiantes de una de esas muestras esté comprendida entre 6,3 y 6,8 puntos.

Resolución
  1. El tamaño de la población es 250+300+400+350=1.300. Llamamos 𝑥 al número de individuos en la muestra del segundo estrato, 𝑦 en la muestra del tercer estrato y 𝑧 en la muestra del cuarto estrato. Como se usa afijación proporcional y se seleccionan 20 individuos del primer estrato, 25020=300𝑥=400𝑦=350𝑧. Despejamos estos valores. 25020=300𝑥⇔𝑥=20⋅300250=24,25020=400𝑦⇔𝑦=20⋅400250=32,25020=350𝑧⇔𝑧=20⋅350250=28. Por tanto, se seleccionan 24 individuos del segundo estrato, 32 del tercer estrato y 28 del cuarto estrato. Así que el tamaño de la muestra es 20+24+32+28=104.
    1. La distribución de las medias muestrales ――𝑋 sigue una normal 𝑁(𝜇,𝜎√𝑛) con 𝜇 =6,4, 𝜎 =0,7 y 𝑛 =49. Es decir, ――𝑋 ∼𝑁(6,4;0,1).
    2. Calculamos la probabilidad. 𝑃(6,3≤――𝑋≤6,8)=𝑃(6,3−6,40,1≤𝑍≤6,8−6,40,1)=𝑃(−1≤𝑍≤4)=𝑃(𝑍≤4)−𝑃(𝑍≤−1)==𝑃(𝑍≤4)−(1−𝑃(𝑍≤1))≈0,8413.

Ejercicio 8

Se desea estimar la proporción de donantes de sangre en una universidad. Para ello se toma una muestra aleatoria de 400 personas de esa universidad, resultando que 64 son donantes de sangre.

  1. Calcule un intervalo de confianza, con un nivel del 98%, para estimar la proporción poblacional de donantes de sangre.
  2. Si el nivel de confianza es del 95%, calcule el error máximo cometido. Razone si este error será mayor o menor al disminuir el nivel de confianza.

Resolución
  1. Como 64 personas de 𝑛 =400 son donantes de sangre, la proporción muestral es: 𝑝=64400=0,16. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 98%, entonces: 𝛼=1−0,98=0,02⇒1−𝛼2=1−0,022=0,99⇒𝑧𝛼/2=2,325. Por tanto, el intervalo de confianza para estimar la proporción poblacional de donantes de sangre con un nivel de confianza del 98% es: 𝐼=(0,16−2,325⋅√0,16⋅(1−0,16)400,0,16+2,325⋅√0,16⋅(1−0,16)400)≈(0,1174;0,2026).
  2. Si el nivel de confianza es del 95%, entonces: 𝛼=1−0,95=0,05⇒1−𝛼2=1−0,052=0,975⇒𝑧𝛼/2=1,96. Por tanto, el error máximo cometido es: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=1,96⋅√0,16⋅(1−0,16)400≈0,0359. El error máximo cometido disminuye al reducir el nivel de confianza, porque el intervalo tiene una menor amplitud.