Icono Matemáticas de Selectividad

Buscar GitHub

Ejercicio 2: Junio de 2025

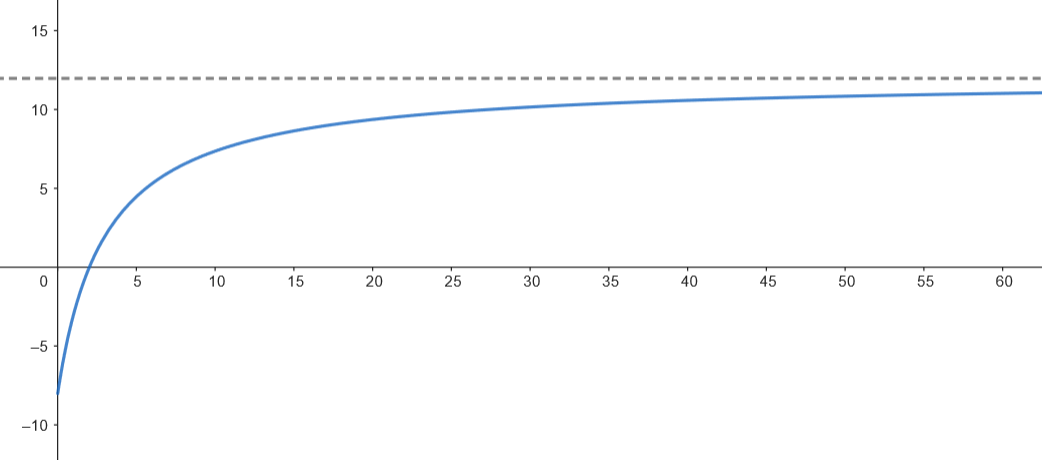
Un periódico digital ha publicado una noticia de última hora. El número de personas que han visto la noticia 𝑡 horas después de su lanzamiento viene modelado por la función: 𝑁(𝑡)=500.000⋅(1−𝑒−0,2𝑡),𝑡>0.

  1. Estudie la monotonía y curvatura de la función 𝑁.
  2. Represente gráficamente la función 𝑁 y describa su tendencia a lo largo del tiempo.
  3. ¿Cuánto tiempo ha debido de pasar para que la noticia haya sido vista por 450.000 personas?
  4. La velocidad de difusión de la noticia (número de personas por hora que han visto la publicación) es 𝑁′(𝑡). ¿Qué conclusión se obtiene al comparar 𝑁′(𝑡) en los instantes 𝑡 =1 y 𝑡 =10?

Resolución
  1. En primer lugar, hallamos las dos primeras derivadas de la función 𝑁. 𝑁′(𝑡)=500.000⋅(−𝑒−0,2𝑡)⋅(−0,2)=100.000𝑒−0,2𝑡,𝑁″(𝑡)=100.000𝑒−0,2𝑡⋅(−0,2)=−20.000𝑒−0,2𝑡.
    • Observamos que 𝑁′(𝑡) >0 para 𝑡 >0, así que 𝑁 es creciente en todo su dominio.
    • Observamos que 𝑁″(𝑡) <0 para 𝑡 >0, así que 𝑁 es cóncava en todo su dominio.
  2. Veamos si la gráfica de la función tiene asíntota horizontal para estudiar su tendencia. lím𝑡→+∞⁡𝑁(𝑡)=lím𝑡→+∞⁡500.000(1−𝑒−0,2𝑡)=500.000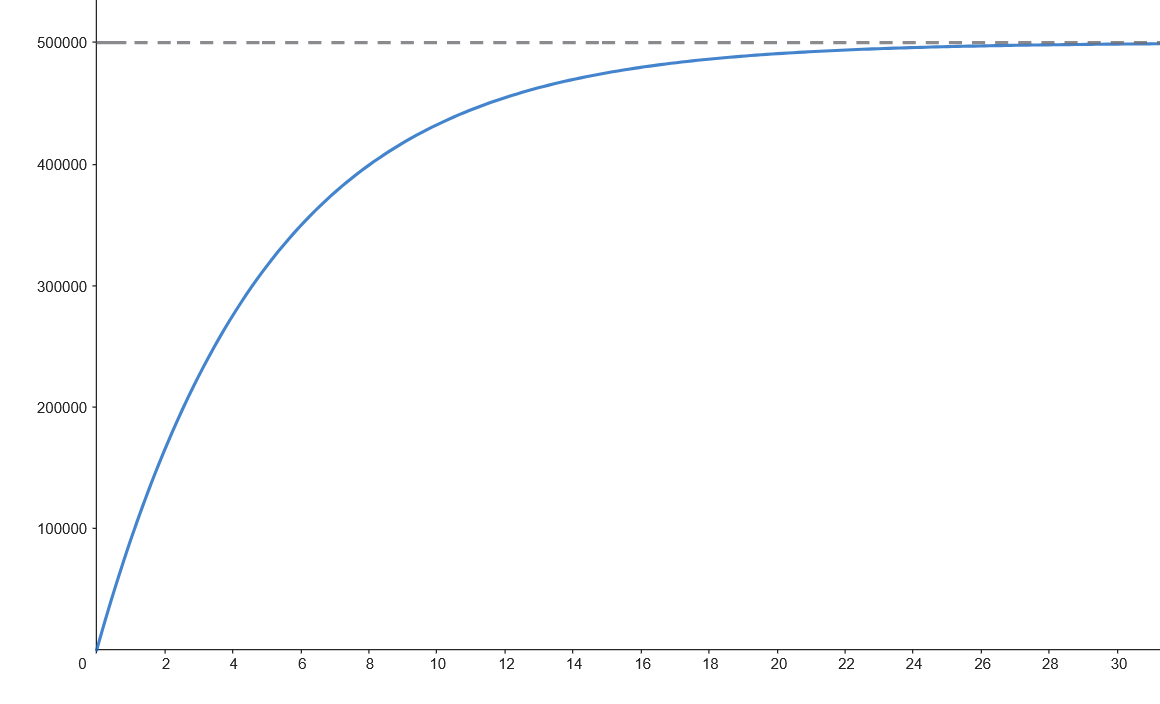. Por tanto, la recta 𝑦 =500.000 es una asíntota horizontal. Representamos gráficamente la función usando esta información. Figura Podemos observar que el número de personas que ven la noticia aumenta rápidamente en las primeras horas y se va acercando a 500.000, cada vez con menor velocidad.
  3. Para que la noticia haya sido vista por 450.000 personas ha de verificarse que: 𝑁(𝑡)=450.000⇔500.000(1−𝑒−0,2𝑡)=450.000⇔1−𝑒−0,2𝑡=910⇔𝑒−0,2𝑡=110⇔⇔−0,2𝑡=ln⁡(110)⇔𝑡=−ln⁡(110)0,2=5ln⁡(10)≈11,5129. Por tanto, han debido de pasar un poco más de 11 horas y media.
  4. Calculamos el valor de la derivada en los dos instantes. 𝑁′(1)≈81.873,0753,𝑁′(10)≈13.533,5283. Observamos que la velocidad de difusión de la noticia se reduce en gran medida con el paso de las horas.

Ejercicio 3: Reserva 2 de 2024

Se considera la función 𝑓(𝑥)=1−43+𝑥.

  1. Halle el dominio de 𝑓 y los puntos de corte de su gráfica con los ejes de coordenadas.
  2. Calcule las asíntotas de la función 𝑓.
  3. Obtenga los puntos donde la recta tangente a la gráfica de 𝑓 tiene pendiente 1.
  4. Estudie la curvatura de la función 𝑓.

Resolución
    • La función 𝑓 es una función racional, así que los puntos que no pertenecen al dominio son aquellos que anulan el denominador. 3+𝑥=0⇔𝑥=−3. Por tanto, Dom⁡(𝑓) =ℝ ∖{ −3}.
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑓(𝑥)=0⇔1−43+𝑥=0⇔1=43+𝑥⇔3+𝑥=4⇔𝑥=1. Luego el único punto de corte con el eje 𝑋 es (1,0).
    • Hallamos ahora el punto de corte con el eje 𝑌. 𝑓(0)=1−43=−13. Así que el punto de corte con el eje 𝑌 es (0,−13).
    • El denominador se anula en 𝑥 = −3 y observamos que lím𝑥→−3−⁡𝑓(𝑥)=lím𝑥→−3−⁡(1−43+𝑥)=+∞,lím𝑥→−3+⁡𝑓(𝑥)=lím𝑥→−3+⁡(1−43+𝑥)=−∞. Por tanto, la recta 𝑥 = −3 es una asíntota vertical.
    • Veamos si tiene una asíntota horizontal. lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡(1−43+𝑥)=1. Por tanto, la recta 𝑦 =1 es una asíntota horizontal.
  3. En primer lugar, hallamos la derivada de la función 𝑓. 𝑓′(𝑥)=4(3+𝑥)2. La pendiente de la recta tangente viene dada por el valor de la derivada. Así que: 𝑓′(𝑥)=1⇔4(3+𝑥)2=1⇔4=(3+𝑥)2⇔{3+𝑥=2⇔𝑥=−1,3+𝑥=−2⇔𝑥=−5. Por tanto, la recta tangente tiene pendiente 1 en los puntos de abscisa 𝑥 = −1 y 𝑥 = −5.
  4. En primer lugar, hallamos la segunda derivada de la función 𝑓. 𝑓″(𝑥)=−8(3+𝑥)3. Observamos que 𝑓″(𝑥) ≠0 para 𝑥 ≠ −3, así que no tiene puntos de inflexión. Estudiamos el signo de 𝑓″ considerando 𝑥 = −3 por no pertenecer al dominio.
    • Si 𝑥 < −3, 𝑓″(𝑥) >0. Así que 𝑓 es convexa.
    • Si 𝑥 > −3, 𝑓″(𝑥) <0. Así que 𝑓 es cóncava.
    Por tanto, 𝑓 es convexa en ( −∞, −3) y cóncava en ( −3, +∞).

Ejercicio 3: Junio de 2023

Se considera la función 𝑓(𝑥) =𝑥3 −3𝑥2 +2𝑥.

  1. Halle los puntos de corte con los ejes, los intervalos de crecimiento y decrecimiento, los extremos relativos de 𝑓 y su curvatura.
  2. Represente gráficamente la función 𝑓.
  3. Calcule el área del recinto acotado, limitado por la gráfica de 𝑓 y el eje de abscisas.

Resolución
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑓(𝑥)=0⇔𝑥3−3𝑥2+2𝑥=0⇔𝑥(𝑥2−3𝑥+2)=0⇔⎧{ {⎨{ {⎩𝑥=0,𝑥2−3𝑥+2=0⇔{𝑥=1,𝑥=2. Luego los puntos de corte con el eje 𝑋 son (0,0), (1,0) y (2,0). Observamos que (0,0) es por tanto el punto de corte con el eje 𝑌.
    • Estudiamos la monotonía y los extremos. En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=3𝑥2−6𝑥+2. Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔3𝑥2−6𝑥+2=0⇔𝑥=3±√33=1±√33. Estudiemos el signo de la derivada.
      (−∞,1−√33) (1−√33,1+√33) (1+√33,+∞)
      signo de 𝑓′ + − +
      monotonía de 𝑓 → → →
      Por tanto, 𝑓 es creciente en (−∞,1−√33) ∪(1+√33,+∞) y es decreciente en (1−√33,1+√33). Además, tiene un máximo relativo en 𝑥 =1 −√33 y un mínimo relativo en 1 +√33. Es decir, el punto (0,42; 0,38) es un máximo relativo y el punto (1,58; −0,38) es un mínimo relativo.
    • Estudiamos la curvatura. Para ello, calculamos la segunda derivada de 𝑓. 𝑓″(𝑥)=6𝑥−6. Para hallar los candidatos a puntos de inflexión, igualamos la segunda derivada a cero. 𝑓″(𝑥)=0⇔6𝑥−6=0⇔𝑥=1. Estudiemos el signo de la segunda derivada.
      ( −∞,1) (1, +∞)
      signo de 𝑓″ − +
      curvatura de 𝑓 ⌢ ⌣
      Por tanto, 𝑓 es convexa en (1, +∞) y es cóncava en ( −∞,1). Además, tiene un punto de inflexión en 𝑥 =1, es decir, el punto (1,0).
  2. Representamos gráficamente la función usando la información del apartado anterior. Figura
  3. Podemos representar el recinto acotado limitado por la gráfica de 𝑓 y el eje 𝑋. Figura Calculamos el área. ∫10𝑓(𝑥)𝑑𝑥+∫21−𝑓(𝑥)𝑑𝑥=∫10(𝑥3−3𝑥2+2𝑥)𝑑𝑥+∫21−(𝑥3−3𝑥2+2𝑥)𝑑𝑥==[14𝑥4−𝑥3+𝑥2]10−[14𝑥4−𝑥3+𝑥2]21=14−(−14)=12𝑢2.

Ejercicio 4: Julio de 2023

Sea la función 𝑓(𝑡)=12𝑡−24𝑡+3,𝑡≥0.

  1. Represente gráficamente la función 𝑓, determinando los puntos de corte con los ejes coordenados y las ecuaciones de las asíntotas, y estudiando la monotonía y la curvatura de 𝑓.
  2. Si la función 𝑓 representa los beneficios de una empresa, en millones de euros, donde 𝑡 indica los años de vida de la empresa:
    1. ¿A partir de qué año la empresa deja de tener pérdidas? Justifique la respuesta.
    2. A medida que pasan los años, ¿están limitados los beneficios? En caso afirmativo, ¿cuál es su límite y por qué?

Resolución
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑓(𝑡)=0⇔12𝑡−24𝑡+3=0⇔12𝑡−24=0⇔𝑡=2. Luego el punto de corte con el eje 𝑋 es (2,0).
    • Hallamos ahora el punto de corte con el eje 𝑌. 𝑓(0)=−243=−8. Así que el punto de corte con el eje 𝑌 es (0, −8).
    • Estudiamos las asíntotas. El denominador solo se anula en 𝑡 = −3. Sin embargo, la función no está definida en un entorno cercano, así que no tiene ninguna asíntota vertical. Veamos si 𝑓 tiene alguna asíntota horizontal. lím𝑡→+∞⁡12𝑡−24𝑡+3=12. Por tanto, la recta 𝑦 =12 es una asíntota horizontal.
    • Estudiamos la monotonía. En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑡)=12(𝑡+3)−(12𝑡−24)(𝑡+3)2=60(𝑡+3)2. Observamos que la derivada nunca se anula y siempre es positiva, así que no tiene puntos críticos y es creciente en todo su dominio.
    • Estudiamos la curvatura. Para ello, calculamos la segunda derivada de 𝑓. 𝑓″(𝑡)=−120(𝑡+3)3. Observamos que la segunda derivada nunca se anula y es siempre negativa para 𝑡 ≥0, así que no tiene puntos de inflexión y es cóncava en todo su dominio.
    Representamos gráficamente la función usando esta información. Figura
    1. Los beneficios de la empresa empiezan a ser positivos a partir del segundo año, donde se encuentra el punto de corte (2,0).
    2. A pesar de que los beneficios aumentan con el paso de los años, tienen como límite 12 millones de euros, representado en la gráfica por la asíntota horizontal 𝑦 =12.

Ejercicio 4: Reserva 1 de 2022

Se considera la función 𝑓(𝑥)=𝑥−3𝑥+2.

  1. Determine el dominio de la función y estudie su monotonía y curvatura.
  2. Calcule las ecuaciones de las asíntotas de 𝑓 si existen. Calcule los puntos de corte de la gráfica de 𝑓 con los ejes de coordenadas.
  3. Represente la gráfica de la función 𝑓.

Resolución
    • La función 𝑓 es una función racional, así que los puntos que no pertenecen al dominio son aquellos que anulan al denominador. 𝑥+2=0⇔𝑥=−2. Por tanto, Dom⁡(𝑓) =ℝ ∖{ −2}.
    • Estudiamos la monotonía. En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=𝑥+2−(𝑥−3)(𝑥+2)2=5(𝑥+2)2. Observamos que 𝑓′(𝑥) >0 para 𝑥 ≠ −2, así que 𝑓 es creciente en todo su dominio y no tiene extremos.
    • Estudiamos la curvatura. Para ello, calculamos la segunda derivada de 𝑓. 𝑓″(𝑥)=−10(𝑥+2)3. Observamos que 𝑓″(𝑥) ≠0 para 𝑥 ≠ −2, así que no tiene puntos de inflexión. Estudiamos el signo de la segunda derivada, considerando 𝑥 = −2 por no pertenecer al dominio.
      ( −∞, −2) ( −2, +∞)
      signo de 𝑓″ + −
      curvatura de 𝑓 ⌣ ⌢
      Por tanto, la función es convexa en ( −∞,2) y cóncava en (2, +∞).
    • El denominador se anula en 𝑥 = −2 y observamos que lím𝑥→−2−⁡𝑓(𝑥)=lím𝑥→−2−⁡𝑥−3𝑥+2=+∞,lím𝑥→−2+⁡𝑓(𝑥)=lím𝑥→−2+⁡𝑥−3𝑥+2=−∞. Por tanto, la recta 𝑥 = −2 es una asíntota vertical.
    • Veamos si tiene una asíntota horizontal. lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡𝑥−3𝑥+2=1. Por tanto, la recta 𝑦 =1 es una asíntota horizontal.
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑓(𝑥)=0⇔𝑥−3𝑥+2=0⇔𝑥−3=0⇔𝑥=3. Luego el único punto de corte con el eje 𝑋 es (3,0).
    • Hallamos ahora el punto de corte con el eje 𝑌. 𝑓(0)=−32. Así que el punto de corte con el eje 𝑌 es (0,−32).
  3. Representamos gráficamente la función usando la información de los apartados anteriores. Figura

Ejercicio 4: Reserva 1 de 2020

Se considera la función 𝑓(𝑥)=⎧{ {⎨{ {⎩𝑥2+𝑥+1,si 𝑥≤0,11−𝑥,si 𝑥>0.

  1. Estudie la continuidad y derivabilidad de 𝑓 en 𝑥 =0.
  2. Estudie la monotonía y curvatura de 𝑓 en su dominio.
  3. Calcule las ecuaciones de las asíntotas de 𝑓.

Ejercicio A2: Junio de 2019

Se considera la función 𝑓(𝑥) =𝑥3 −9𝑥 +2.

  1. Obtenga las ecuaciones de las rectas tangentes a la gráfica de la función que sean paralelas a la recta 𝑦 =3𝑥 −3.
  2. Estudie la monotonía y la curvatura de la función 𝑓.
  3. Calcule ∫𝑓(𝑥)𝑑𝑥.

Ejercicio B2: Junio de 2019

Sea la función 𝑓(𝑥)=⎧{ {⎨{ {⎩1𝑥−1,si 𝑥<0,𝑥2+𝑎,si 𝑥≥0.

  1. Determine el valor del parámetro 𝑎 para que 𝑓 sea continua en todo su dominio. Para ese valor de 𝑎, estudie la derivabilidad de 𝑓.
  2. Para 𝑎 = −2, estudie la monotonía y curvatura de la función 𝑓. ¿Tiene algún punto de inflexión?

Ejercicio A2: Reserva 3 de 2019

Sea la función 𝑓(𝑥) =𝑥3 +𝑎𝑥2 +𝑏𝑥 +1.

  1. Halle 𝑎 y 𝑏 de forma que 𝑓 tenga un extremo relativo en 𝑥 =1 y la recta tangente a la gráfica de la función 𝑓 en el punto de abscisa 𝑥 =0 tenga pendiente 𝑚 = −1.
  2. Para 𝑎 = −1 y 𝑏 = −1, estudie la monotonía y la curvatura de la función 𝑓.

Ejercicio B2: Reserva 4 de 2019

Se considera la función 𝑓(𝑥) =13𝑥3 −2𝑥2 +3𝑥 +1.

  1. Estudie su monotonía y halle sus extremos relativos.
  2. Determine los intervalos de concavidad y convexidad. Calcule su punto de inflexión.
  3. Calcule la pendiente de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0.
  4. Calcule ∫𝑓(𝑥)𝑑𝑥.

Ejercicio B2: Septiembre de 2019

De una cierta función 𝑓, sabemos que su función derivada es 𝑓′(𝑥) =3𝑥2 −3.

  1. Estudie los intervalos de crecimiento y decrecimiento de 𝑓, y calcule la abscisa de sus extremos relativos.
  2. Determine la curvatura de 𝑓 y halle la abscisa de su punto de inflexión.
  3. Calcule la función 𝑓, sabiendo que su gráfica pasa por el punto ( −1,3).

Ejercicio B2: Reserva 4 de 2017

Se considera la función 𝑓(𝑥)={𝑎𝑥−3𝑥2,si 𝑥≤1,2𝑥2+𝑏,si 𝑥>1.

  1. Calcule los valores de 𝑎 y 𝑏 para que la función 𝑓 sea derivable en 𝑥 =1.
  2. Para 𝑎 =3 y 𝑏 = −2, estudie la monotonía y curvatura de la función 𝑓.

Ejercicio A2: Septiembre de 2017

Sea la función 𝑓(𝑥) =𝑥3 +𝑎𝑥2 +𝑏𝑥.

  1. Halle 𝑎 y 𝑏 sabiendo que la función tiene un mínimo en el punto de abscisa 𝑥 = −1 y un punto de inflexion en el punto de abscisa 𝑥 = −2.
  2. Para 𝑎 =6 y 𝑏 =9, halle los puntos de corte con los ejes, estudie la monotonía y extremos y esboce la gráfica de la función.

Ejercicio B2: Reserva 4 de 2016

Se considera la función 𝑓(𝑥)=⎧{ {⎨{ {⎩4𝑥,si 𝑥≤2,𝑥2−2𝑥+2,si 𝑥>2.

  1. Estudie la continuidad y la derivabilidad de esta función.
  2. Estudie su monotonía y su curvatura para 𝑥 >0.

Ejercicio B2: Reserva 3 de 2015

Se considera la función 𝑓(𝑥) =𝑥3 −2𝑥2 +𝑥.

  1. Halle el máximo, el mínimo y el punto de inflexión de la función.
  2. Calcule los puntos de corte con los ejes.
  3. Obtenga las ecuaciones de las rectas tangentes a la gráfica de 𝑓 en los puntos de abscisas 𝑥 =0 y 𝑥 =1.

Ejercicio A2: Septiembre de 2015

  1. Determine el valor de 𝑎 para que sea continua en 𝑥 = −1 la función 𝑓(𝑥)={𝑎𝑥𝑥−1,si 𝑥≤−1,𝑥3−3𝑥2+6𝑥−2,si 𝑥>−1.
  2. Calcule los coeficientes 𝑏 y 𝑐 de la función 𝑔(𝑥) =𝑥3 +𝑏𝑥2 +𝑐𝑥 −2 para que (1,2) sea un punto de inflexión de 𝑔.

Ejercicio B2: Septiembre de 2015

Sea la función 𝑓(𝑥) =𝑥3 −9𝑥2 +8.

  1. Halle las coordenadas de sus extremos relativos y de su punto de inflexión, si existen.
  2. Determine la ecuación de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =1.

Ejercicio A2: Reserva 1 de 2014

Sea la función 𝑓(𝑥) =𝑥3 −3𝑥2 +3𝑥.

  1. Estudie la monotonía de 𝑓 y halle los extremos relativos que posea.
  2. Estudie su curvatura y calcule su punto de inflexión.
  3. Represente la gráfica de la función 𝑓.

Ejercicio B2: Reserva 4 de 2014

Represente gráficamente la función 𝑓(𝑥) =𝑥3 −6𝑥2 +12𝑥, estudiando previamente su dominio, puntos de corte con los ejes, intervalos de monotonía, extremos, intervalos de concavidad y convexidad y puntos de inflexión.

Ejercicio B2: Reserva 3 de 2013

Sea la función 𝑓(𝑥) =𝑥3 −24𝑥2 +4𝑥.

  1. Halle los intervalos de concavidad y convexidad y los puntos de inflexión.
  2. Obtenga la ecuación de la recta tangente a la gráfica de 𝑓(𝑥) en el punto de abscisa 𝑥 = −2.
  3. En el punto de abscisa 𝑥 =1, ¿la función es creciente o decreciente?

Ejercicio B2: Reserva 4 de 2013

Se considera la función 𝑓(𝑥)={𝑥3−1,si 𝑥<1,−𝑥2+4𝑥−3,si 𝑥≥1.

  1. Determine el dominio y estudie la continuidad de la función.
  2. Obtenga los extremos de la función.
  3. Estudie su curvatura.

Ejercicio A2: Reserva 1 de 2012

De la función 𝑓 se sabe que su función derivada es 𝑓′(𝑥) =3𝑥2 −8𝑥 +5.

  1. Estudie la monotonía y la curvatura de 𝑓.
  2. Sabiendo que la gráfica de 𝑓 pasa por el punto (1,1), calcule la ecuación de la recta tangente en dicho punto.

Ejercicio A2: Reserva 3 de 2012

Se considera la función 𝑓(𝑥)=1−2𝑥+2.

  1. Determine la monotonía y curvatura de la función.
  2. Calcule sus asíntotas.
  3. Represéntela gráficamente.

Ejercicio A2: Septiembre de 2011

  1. Halle el dominio, los puntos de corte con los ejes y las asíntotas de la función: 𝑓(𝑥)=4𝑥2𝑥+1.
  2. Halle los intervalos de monotonía, los extremos relativos, los intervalos de curvatura y los puntos de inflexión de la función: 𝑔(𝑥)=𝑥3+3𝑥2+3𝑥.