Ejercicio 4: Reserva 2 de 2025
Se considera la función
- Estudie la continuidad y derivabilidad de
𝑓 𝑥 = − 2 - Calcule la ecuación de la recta tangente a la gráfica de la función
𝑓 -
Represente la región del plano acotada superiormente por la gráfica de
𝑓
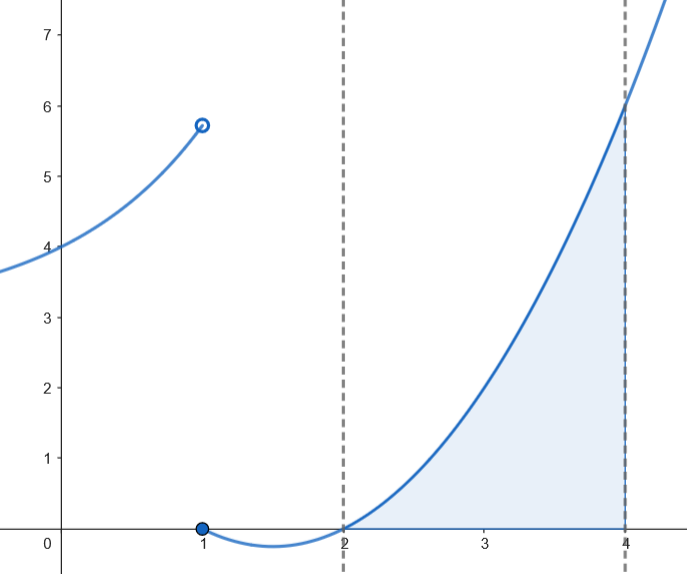 Calculamos el área.
Calculamos el área.