Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 2 de 2021

Ejercicio 1

Un laboratorio farmacéutico tiene una línea de producción con dos medicamentos A y B, con marca comercial y genérico respectivamente, de los cuales, entre los dos como máximo puede fabricar 10 unidades a la hora. Desde el punto de vista del rendimiento, se han de producir al menos 4 unidades por hora entre los dos y por motivos de política sanitaria, la producción de A ha de ser como mucho 2 unidades más que la de B. Cada unidad de tipo A que vende le produce un beneficio de 60 euros, mientras que cada unidad de tipo B le produce un beneficio de 25 euros. Si se vende todo lo que se produce, determine las unidades de cada medicamento que deberá fabricar por hora para maximizar su beneficio y obtenga el valor de dicho beneficio.

Resolución

Llamamos 𝑥 al número de unidades del medicamento A e 𝑦 al número de unidades del medicamento B. Las restricciones del problema son: ⎧{ { {⎨{ { {⎩𝑥+𝑦≤10,𝑥+𝑦≥4,𝑥≤𝑦+2,𝑥≥0. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=60𝑥+25𝑦.

Representamos la región factible. 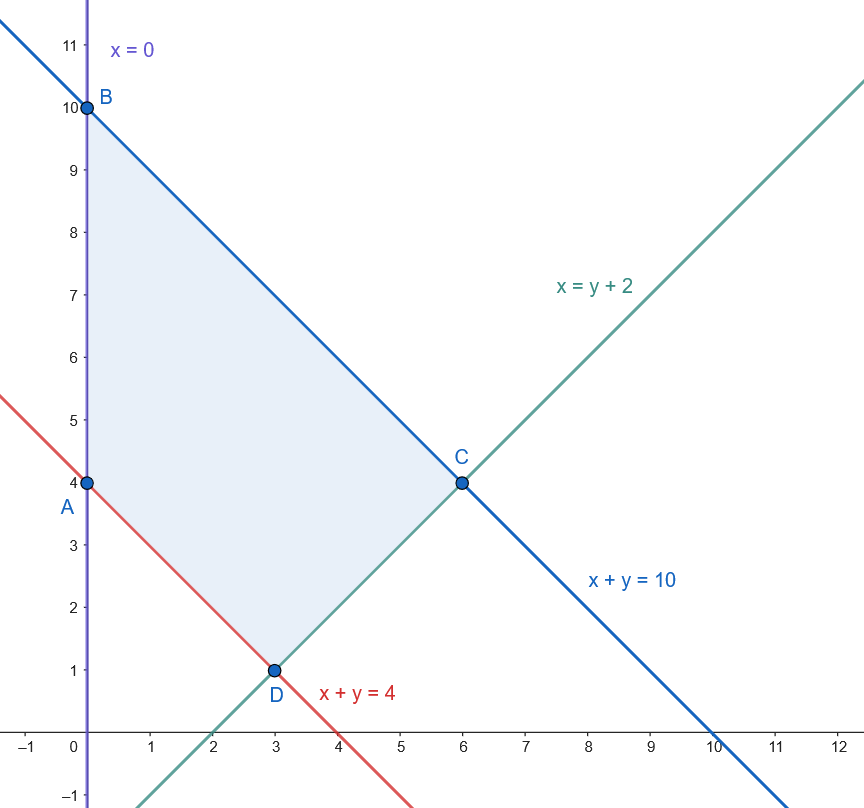Figura Los vértices son: 𝐴(0,4),𝐵(0,10),𝐶(6,4)y𝐷(3,1).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(0,4)=100,𝐹(𝐵)=𝐹(0,10)=250,𝐹(𝐶)=𝐹(6,4)=460,𝐹(𝐷)=𝐹(3,1)=205. Por tanto, el beneficio máximo se alcanza fabricando 6 unidades del medicamento A y 4 del medicamento B por hora, con unas ganancias de 460€.

Ejercicio 2

Se consideran las matrices 𝐴=(𝑎468),𝐵=(2233)y𝐶=(12).

  1. Calcule el valor del parámetro 𝑎 para que la matriz 𝐴 no tenga inversa.
  2. Para 𝑎 =3, resuelva la ecuación matricial 𝑋𝐴 −𝑋𝐵 =𝐶.
  3. Para 𝑎 =3, compruebe que 𝐴2 =11𝐴 y exprese 𝐴8 en función de la matriz 𝐴.

Resolución
  1. Calculamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣𝑎468∣=8𝑎−24. La inversa de 𝐴 existe si y solo si su determinante es no nulo. Observamos que: |𝐴|=0⇔8𝑎−24=0⇔𝑎=3. Por tanto, 𝐴 no tiene inversa cuando 𝑎 =3.
  2. Despejamos la ecuación matricial. 𝑋𝐴−𝑋𝐵=𝐶⇔𝑋(𝐴−𝐵)=𝐶⇔𝑋=𝐶(𝐴−𝐵)−1. En primer lugar, calculamos la matriz 𝐴 −𝐵 y hallamos su determinante. 𝐴−𝐵=(3468)−(2233)=(1235)⇒|𝐴−𝐵|=∣1235∣=−1. Como det(𝐴 −𝐵) ≠0, la matriz 𝐴 −𝐵 es invertible. Para hallar su inversa, calculamos primero su matriz adjunta. Adj⁡(𝐴−𝐵)=(5−3−21). Calculamos su inversa de la forma: (𝐴−𝐵)−1=1|𝐴−𝐵|Adj⁡(𝐴−𝐵)𝑡=−(5−2−31)=(−523−1). Por tanto, 𝑋=𝐶(𝐴−𝐵)−1=(12)(−523−1)=(10).
  3. Calculamos la matriz 𝐴2: 𝐴2=𝐴⋅𝐴=(3468)(3468)=(33446688)=11𝐴. Por tanto, 𝐴8=(𝐴2)4=(11𝐴)4=114𝐴4=114⋅(𝐴2)2=114⋅(11𝐴)2=114⋅112𝐴2=116⋅11𝐴=117𝐴.

Ejercicio 3

Se considera la función 𝑓(𝑥)={(𝑥+1)2,si −2≤𝑥<0,(𝑥−1)2,si 0≤𝑥≤2.

  1. Estudie la continuidad y derivabilidad de la función 𝑓 en todo su dominio.
  2. Calcule los extremos de la función 𝑓.
  3. Represente el recinto que encierra la gráfica de 𝑓, las rectas 𝑥 = −1, 𝑥 =1 y el eje 𝑂𝑋. Calcule el área de dicho recinto.

Resolución
  1. Estudiamos la continuidad y la derivabilidad.
    • Si 𝑥 ∈[ −2,2] con 𝑥 ≠0, 𝑓 es continua y derivable con: 𝑓′(𝑥)={2(𝑥+1),si −2≤𝑥<0,2(𝑥−1),si 0<𝑥≤2.
    • Estudiamos la continuidad en 𝑥 =0. lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0−⁡(𝑥+1)2=1,lím𝑥→0+⁡𝑓(𝑥)=lím𝑥→0+⁡(𝑥−1)2=1,𝑓(0)=1. Observamos que: lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0+⁡𝑓(𝑥)=𝑓(0). Así que 𝑓 es continua en 𝑥 =0. Pasamos a estudiar su derivabilidad. 𝑓′−(0)=lím𝑥→0−⁡𝑓′(𝑥)=lím𝑥→0−⁡2(𝑥+1)=2,𝑓′+(0)=lím𝑥→0+⁡𝑓′(𝑥)=lím𝑥→0+⁡2(𝑥−1)=−2. Como 𝑓′−(0) ≠𝑓′+(0), 𝑓 no es derivable en 𝑥 =0.
    Por tanto, 𝑓 es continua en [ −2,2] y derivable en [ −2,0) ∪(0,2].
  2. Para hallar los puntos críticos, igualamos las dos ramas de la derivada a cero.
    • Si −2 ≤𝑥 <0, 𝑓′(𝑥)=0⇔2(𝑥+1)=0⇔𝑥=−1.
    • Si 0 <𝑥 ≤2, 𝑓′(𝑥)=0⇔2(𝑥−1)=0⇔𝑥=1.
    Así que los puntos críticos son 𝑥 = −1 y 𝑥 =1. Consideramos también 𝑥 =0 por no ser derivable. Estudiamos el signo de la derivada.
    ( −2, −1) ( −1,0) (0,1) (1,2)
    signo de 𝑓′ − + − +
    monotonía de 𝑓 → → → →
    Por tanto, los puntos ( −2,1), (0,1) y (2,1) son máximos relativos y los puntos ( −1,0) y (1,0) son mínimos relativos.
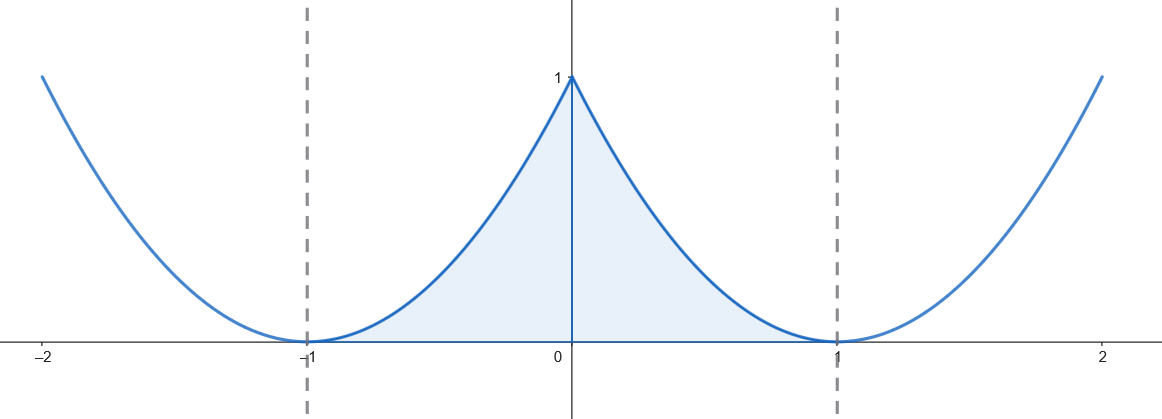  3. Representamos el recinto. Figura Como el recinto es simétrico, podemos calcular su área como: 2∫10(𝑥−1)2𝑑𝑥=2[13(𝑥−1)3]10=2⋅13=23𝑢2.

Ejercicio 4

  1. Sea 𝑓 una función de la que sabemos que la gráfica de su derivada, 𝑓′, es una parábola con vértice en el punto (0,8), que corta al eje de abscisas en los puntos ( −4,0) y (4,0).
    1. Dibuje la gráfica de 𝑓′.
    2. A partir de dicha gráfica, halle los intervalos de crecimiento y decrecimiento de 𝑓, así como las abscisas de los extremos relativos de 𝑓.
    3. Sabiendo que la gráfica de 𝑓 pasa por el origen de coordenadas, calcule la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0.
  2. Calcule la derivada de la función 𝑔(𝑥) =( −3 +𝑥2)𝑒2𝑥−1.

Resolución
    1. Representamos la gráfica. Figura
    2. La derivada de 𝑓 se anula en 𝑥 = −4 y 𝑥 =4, así que estos son sus puntos críticos. Estudiamos el signo de la derivada.
      ( −∞, −4) ( −4,4) (4, +∞)
      signo de 𝑓′ − + −
      monotonía de 𝑓 → → →
      Por tanto, 𝑓 es creciente en (4,4) y decreciente en ( −∞, −4) y (4,∞). Además, tiene un máximo relativo en 𝑥 =4 y un mínimo relativo en 𝑥 = −4.
    3. Sabemos que 𝑓(0) =0 y 𝑓′(0) =8. La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =0 viene dada por: 𝑦−𝑓(0)=𝑓′(0)(𝑥−0)⇔𝑦=8𝑥.
  2. Calculamos la derivada. 𝑔′(𝑥)=2𝑥𝑒2𝑥−1+(−3+𝑥2)𝑒2𝑥−1⋅2=2(𝑥2+𝑥−3)𝑒2𝑥−1.

Ejercicio 5

Un equipo andaluz de baloncesto jugó en una temporada un 40% de los partidos en casa y el resto fuera. De los partidos que jugó en casa, obtuvo un 60% de victorias y el resto fueron derrotas, mientras que de los que jugó fuera, obtuvo un 30% de victorias y el resto derrotas. Se elige un partido de este equipo al azar.

  1. Calcule la probabilidad de que el partido acabase en victoria.
  2. Calcule la probabilidad de que el partido haya sido jugado en casa, sabiendo que el resultado final fue una derrota.
  3. Si además se sabe que el 10% de las victorias obtenidas en casa y el 20% de las obtenidas fuera se produjeron tras una prórroga, calcule la probabilidad de que el partido acabase en victoria y que además esa victoria haya sido tras una prórroga.

Resolución

Llamamos 𝐶 a jugar en casa, 𝐹 a jugar fuera, 𝑉 a obtener una victoria y 𝐷 a obtener una derrota. Podemos hacer un diagrama de árbol.

𝑉
0,6←←←←←←←←←←→
𝐶
0,4←←←←←←←←←←→ 0,4←←←←←←←←←←→
𝐷
𝑉
0,6←←←←←←←←←←→ 0,3←←←←←←←←←←→
𝐹
0,7←←←←←←←←←←→
𝐷
  1. Por el teorema de la probabilidad total, la probabilidad de que el partido acabase en victoria es: 𝑃(𝑉)=𝑃(𝑉∩𝐶)+𝑃(𝑉∩𝐹)=𝑃(𝐶)⋅𝑃(𝑉|𝐶)+𝑃(𝐹)⋅𝑃(𝑉|𝐹)=0,4⋅0,6+0,6⋅0,3=0,42.
  2. La probabilidad de que el partido haya sido jugado en casa sabiendo que el resultado final fue una derrota es: 𝑃(𝐶|𝐷)=𝑃(𝐶∩𝐷)𝑃(𝐷)=𝑃(𝐶)⋅𝑃(𝐷|𝐶)1−𝑃(𝑉)=0,4⋅0,41−0,42≈0,2759.
  3. Llamamos 𝐸 a tener una prórroga. Podemos expandir el diagrama de árbol.
    𝑉 0,2←←←←←←←←←←→ 𝐸
    0,6←←←←←←←←←←→
    𝐶
    0,4←←←←←←←←←←→ 0,4←←←←←←←←←←→
    𝐷
    𝑉 0,1←←←←←←←←←←→ 𝐸
    0,6←←←←←←←←←←→ 0,3←←←←←←←←←←→
    𝐹
    0,7←←←←←←←←←←→
    𝐷
    Por el teorema de la probabilidad total, la probabilidad de que el partido acabase en victoria y que además haya sido tras una prórroga es: 𝑃(𝑉∩𝐸)=𝑃(𝐶∩𝑉∩𝐸)+𝑃(𝐹∩𝑉∩𝐸)=𝑃(𝐶)⋅𝑃(𝑉|𝐶)⋅𝑃(𝐸|𝑉∩𝐶)+𝑃(𝐹)⋅𝑃(𝑉|𝐹)⋅𝑃(𝐸|𝑉∩𝐹)==0,4⋅0,6⋅0,1+0,6⋅0,3⋅0,2=0,06.

Ejercicio 6

Sean 𝐴 y 𝐵 dos sucesos asociados a un mismo espacio muestral con 𝑃(𝐴𝑐) =0,4 y 𝑃(𝐴 ∩𝐵𝑐) =0,12.

  1. Calcule 𝑃(𝐴) y 𝑃(𝐴 ∩𝐵).
  2. Determina 𝑃(𝐵) para que 𝐴 y 𝐵 sean independientes.
  3. Si 𝑃(𝐵𝑐) =0,2, calcule 𝑃(𝐴 ∪𝐵), 𝑃(𝐴𝑐 ∪𝐵𝑐) y 𝑃(𝐴|𝐵𝑐).

Resolución
  1. Calculamos: 𝑃(𝐴)=1−𝑃(𝐴𝑐)=1−0,4=0,6,𝑃(𝐴∩𝐵𝑐)=𝑃(𝐴)−𝑃(𝐴∩𝐵)⇒𝑃(𝐴∩𝐵)=𝑃(𝐴)−𝑃(𝐴∩𝐵𝑐)=0,6−0,12=0,48.
  2. Para que 𝐴 y 𝐵 sean independientes, ha de verificarse que: 𝑃(𝐴∩𝐵)=𝑃(𝐴)⋅𝑃(𝐵)⇔𝑃(𝐵)=𝑃(𝐴∩𝐵)𝑃(𝐴)=0,480,6=0,8.
  3. Como 𝑃(𝐵𝑐) =0,2 ⇔𝑃(𝐵) =0,8, por el apartado anterior sabemos que 𝐴 y 𝐵 son independientes. Calculamos: 𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵)=0,6+0,8−0,48=0,92,𝑃(𝐴𝑐∪𝐵𝑐)=𝑃((𝐴∩𝐵)𝑐)=1−𝑃(𝐴∩𝐵)=1−0,48=0,52,𝑃(𝐴|𝐵𝑐)=𝑃(𝐴)=0,6.

Ejercicio 7

  1. En una población constituida por los números naturales del 1 al 9, ¿cuántas muestras de tamaño 2 se pueden formar por muestreo aleatorio simple? Si se elige al azar una de esas muestras, ¿cuál es la probabilidad de que el valor medio de los dos números de esa muestra sea 5?
  2. Para estimar la proporción de andaluces contagiados por una enfermedad infecciosa en un momento determinado, se ha tomado una muestra de 10.000 personas, resultando que 500 de ellas estaban infectadas.
    1. Con ese dato, establezca un intervalo, al 97% de confianza, para la proporción real de infectados en la población andaluza.
    2. A la vista del intervalo obtenido, razone si se podría aceptar que el 6% de la población andaluza estaba infectada.
    3. Se toma una nueva muestra de mayor tamaño y resulta que hay la misma proporción de positivos en la nueva muestra. Con estos nuevos datos, razone si el nuevo intervalo al 97% de confianza contiene al intervalo anterior o está contenido en él.

Resolución
  1. Con los números naturales del 1 al 9 se pueden formar 9 ⋅9 =81 muestras de tamaño 2. La media de los números es 5 en las muestras (1,9), (2,8), (3,7), (4,6), (5,5), (6,4), (7,3), (8,2) y (9,1). Por tanto la probabilidad es: 𝑝=981=19.
    1. Como 500 personas de 𝑛 =10.000 estaban infectadas, la proporción muestral es: 𝑝=50010.000=0,05. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar la proporción de infectados con un nivel de confianza del 97% es: 𝐼=(0,05−2,17⋅√0,05⋅(1−0,05)10.000,0,05+2,17⋅√0,05⋅(1−0,05)10.000)≈(0,0453;0,0547).
    2. Como 0,06 no pertenece al intervalo de confianza, no puede admitirse como proporción poblacional.
    3. La amplitud del intervalo disminuye al aumentar el tamaño de la muestra, porque el error máximo cometido se reduce. Por tanto, el nuevo intervalo estará contenido en el anterior.

Ejercicio 8

El tiempo, en horas, que los alumnos de un instituto dedican a estudiar para los exámenes finales, se distribuye siguiendo una ley Normal de media desconocida y varianza 81. Se toma una muestra aleatoria de 16 alumnos de dicho instituto, obteniéndose los siguientes tiempos: 30423845526021263344284932514940.

  1. Obtenga un intervalo, con un 95% de confianza, para estimar el tiempo medio de estudio de los alumnos de ese instituto.
  2. Calcule el mínimo tamaño de la muestra que se ha de tomar, para estimar el tiempo medio de estudio de esos alumnos con un error inferior a 2 horas y un nivel de confianza del 98%.

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Calculamos la media muestral. ――𝑥=30+42+38+45+52+60+21+26+33+44+28+49+32+51+49+4016=40. Como el nivel de confianza es del 95%, entonces: 𝛼=1−0,95=0,05⇒1−𝛼2=1−0,052=0,975⇒𝑧𝛼/2=1,96. Por tanto, el intervalo de confianza para estimar el tiempo medio en minutos de estudio de los alumnos con un nivel de confianza del 95% es: 𝐼=(40−1,96⋅√81√16,40+1,96⋅√81√16)=(35,59;44,41).
  2. Si el nivel de confianza es del 98%, entonces: 𝛼=1−0,98=0,02⇒1−𝛼2=1−0,022=0,99⇒𝑧𝛼/2=2,325. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=2,325⋅√81√𝑛=20,925√𝑛. Si se quiere que el error máximo sea inferior a 2, entonces: 20,925√𝑛=2⇔√𝑛=20,9252⇔𝑛=20,925222≈109,4639. Por tanto, el tamaño mínimo de la muestra debe ser de 110 alumnos.