Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 3 de 2024

Ejercicio 1

Se consideran las matrices 𝐴=(1−11−210),𝐵=⎛⎜ ⎜ ⎜⎝0−110−12⎞⎟ ⎟ ⎟⎠y𝐶=⎛⎜ ⎜ ⎜⎝132111031⎞⎟ ⎟ ⎟⎠.

  1. Resuelva la siguiente ecuación 𝐴𝐵𝑋𝐶=(100010).
  2. Halle las dimensiones de las matrices 𝐷 y 𝐸 para que tenga sentido la igualdad 𝐴𝐷 =𝐸𝐵.

Resolución
  1. En primer lugar, hallamos la matriz 𝐴𝐵. 𝐴𝐵=(1−11−210)⎛⎜ ⎜ ⎜⎝0−110−12⎞⎟ ⎟ ⎟⎠=(−2112).
    • Calculamos el determinante de 𝐴𝐵. |𝐴𝐵|=∣−2112∣=−5≠0. Así que 𝐴𝐵 es invertible con det(𝐴𝐵) = −5.
    • Calculamos el determinante de 𝐶. |𝐶|=∣132111031∣=1≠0. Así que 𝐶 es invertible con det(𝐶) =1.
    Despejamos la ecuación matricial. 𝐴𝐵𝑋𝐶=(100010)⇔𝑋=(𝐴𝐵)−1(100010)𝐶−1.
    • Para hallar la inversa de 𝐴𝐵, calculamos primero su matriz adjunta. Adj⁡(𝐴𝐵)=(2−1−1−2). Calculamos su inversa de la forma: (𝐴𝐵)−1=1|𝐴𝐵|Adj⁡(𝐴𝐵)𝑡=−15(2−1−1−2)=15(−2112).
    • Para hallar la inversa de 𝐶, calculamos primero su matriz adjunta. Adj⁡(𝐶)=⎛⎜ ⎜ ⎜⎝−2−1331−311−2⎞⎟ ⎟ ⎟⎠. Calculamos su inversa de la forma: 𝐶−1=1|𝐶|Adj⁡(𝐶)𝑡=⎛⎜ ⎜ ⎜⎝−231−1113−3−2⎞⎟ ⎟ ⎟⎠.
    Por tanto, 𝑋=(𝐴𝐵)−1(100010)𝐶−1=15(−2112)(100010)⎛⎜ ⎜ ⎜⎝−231−1113−3−2⎞⎟ ⎟ ⎟⎠==15(−210120)⎛⎜ ⎜ ⎜⎝−231−1113−3−2⎞⎟ ⎟ ⎟⎠=15(3−5−1−453).
  2. Llamamos 𝑚 ×𝑛 a la dimensión de 𝐷 y 𝑝 ×𝑞 a la de 𝐸. Como la matriz 𝐴 es de dimensión 2 ×3, 𝐷 debe tener 3 filas para poder multiplicarse con ella y el producto 𝐴𝐷 tiene dimensión 2 ×𝑛. Por otro lado, como 𝐵 es de dimensión 3 ×2, 𝐸 debe tener 3 columnas para poder multiplicarse y el producto 𝐸𝐵 tiene dimensión 𝑝 ×2. Por último, para que se cumpla la igualdad se tiene que verificar que 𝑛 =2 y 𝑝 =2. Por tanto, 𝐷 tiene dimensión 3 ×2 y 𝐸 dimensión 2 ×3.

Ejercicio 2

Un centro de bricolaje, que almacena bidones de pintura de interior y de exterior, cuenta con una capacidad máxima de almacenaje de 160 bidones. Por una cuestión logística, en el almacén deben mantenerse al menos 60 bidones, siendo como mínimo 20 bidones de pintura interior. Además, el número de bidones de pintura exterior almacenados no podrá ser inferior al de pintura interior. Se sabe que el gasto diario por almacenar cada bidón de pintura interior es de 1,50€ y por cada bidón de pintura exterior es de 0,90€. Calcule cuántos bidones de cada tipo se deben almacenar para que el gasto diario sea mínimo e indique cuánto supone ese gasto mínimo.

Resolución

Llamamos 𝑥 al número de bidones de pintura de interior e 𝑦 al de bidones de pintura de exterior. Las restricciones del problema son: ⎧{ { {⎨{ { {⎩𝑥+𝑦≤160,𝑥+𝑦≥60,𝑥≥20,𝑦≥𝑥. La función objetivo a minimizar es: 𝐹(𝑥,𝑦)=1,5𝑥+0,9𝑦.

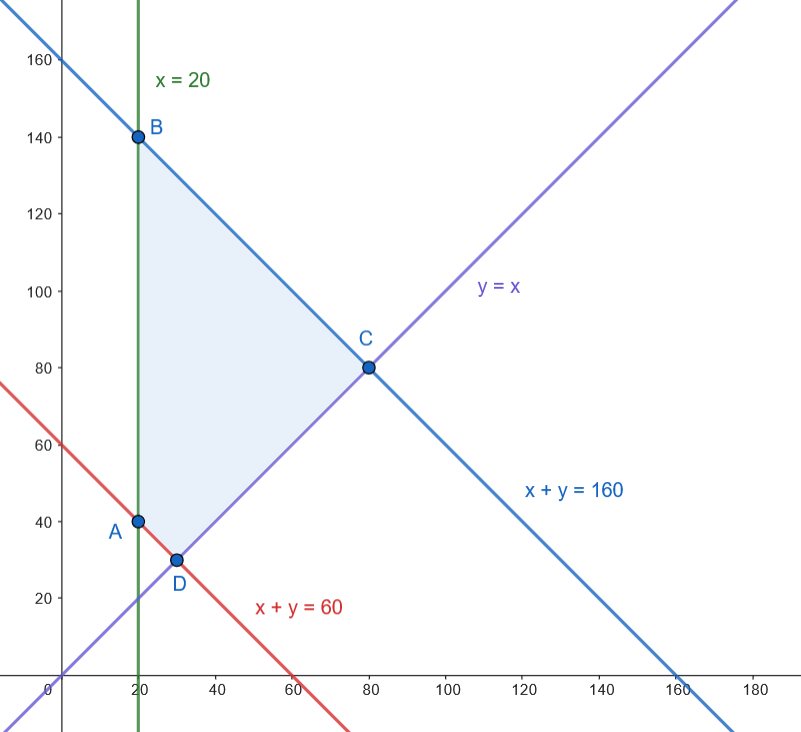Representamos la región factible. Figura Los vértices son: 𝐴(20,40),𝐵(20,140),𝐶(60,60)y𝐷(30,30).

Por el teorema fundamental de la programación lineal, el mínimo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(20,40)=66,𝐹(𝐵)=𝐹(20,140)=156,𝐹(𝐶)=𝐹(60,60)=192,𝐹(𝐷)=𝐹(30,30)=72. Por tanto, el coste diario mínimo se alcanza almacenando 20 bidones de pintura de interior y 40 de exterior, con unos gastos de 66€.

Ejercicio 3

Se desea analizar la evolución de la población de una localidad. Se conoce que la función 𝑓 aproxima el número de habitantes que tiene la población para cada tiempo 𝑡, medido en meses, con 𝑡 ∈[0,60]. El crecimiento de esta población viene dado por la siguiente expresión: 𝑓′(𝑡)=400+30√𝑡. También se sabe que la población en la actualidad, 𝑡 =0, es de 90.000 habitantes.

  1. ¿Cuál será la población dentro de 9 meses?
  2. Calcule ∫169𝑓′(𝑡)𝑑𝑡 e interprete el resultado.
  3. Si se entrega una ayuda de 150€ por cada nuevo habitante durante los tres primeros años, calcule la cuantía total aproximada de la ayuda que recibirá la localidad.

Resolución
  1. En primer lugar, hallamos la función 𝑓 integrando. 𝑓(𝑡)=∫𝑓′(𝑡)𝑑𝑡=∫(400+30√𝑡)𝑑𝑡=400𝑡+30⋅23𝑡32+𝐶=400𝑡+20√𝑡3+𝐶. Como la población en 𝑡 =0 es de 90.00 habitantes, ha de verificarse que: 𝑓(0)=90.000⇔𝐶=90.000. Así que: 𝑓(𝑡)=400𝑡+20√𝑡3+90.000. Por tanto, la población dentro de 9 meses será de 𝑓(9) =94.140 habitantes.
  2. Calculamos la integral. ∫169𝑓′(𝑡)𝑑𝑡=[400𝑡+20√𝑡3]169=400⋅16+20⋅64−(400⋅9+20⋅27)=3.540. El resultado se corresponde con el incremento del número de habitantes entre los meses 9 y 16.
  3. El número de nuevos habitantes durante los tres primeros años viene dado por: 𝑓(36)−𝑓(0)=108.720−90.000=18.720. Por tanto, la ayuda que recibirá la localidad es de 18.720 ⋅150 =2.808.000€.

Ejercicio 4

Se considera la función 𝑓(𝑥)={3+𝑒𝑥,si 𝑥<1,𝑥2+𝑎𝑥+2,si 𝑥≥1.

  1. Determine el valor de 𝑎 para que la función 𝑓 sea continua en ℝ. Para ese valor de 𝑎, ¿es 𝑓 derivable?
  2. Para 𝑎 = −3, calcule la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0.
  3. Para 𝑎 = −3, represente la región limitada por la gráfica de 𝑓, las rectas 𝑥 =2, 𝑥 =4 y el eje de abscisas. Calcule el área de dicha región.

Resolución
  1. Si 𝑥 ≠1, 𝑓 es continua y derivable para cualquier valor de 𝑎 con: 𝑓′(𝑥)={𝑒𝑥,si 𝑥<1,2𝑥+𝑎,si 𝑥>1. Estudiamos su continuidad en el punto de ruptura 𝑥 =1. lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡(3+𝑒𝑥)=3+𝑒,lím𝑥→1+⁡𝑓(𝑥)=lím𝑥→1+⁡(𝑥2+𝑎𝑥+2)=3+𝑎,𝑓(1)=3+𝑎. Para que 𝑓 sea continua, ha de verificarse que: 3+𝑒=3+𝑎⇔𝑎=𝑒. Estudiamos la derivabilidad. 𝑓′−(1)=lím𝑥→1−⁡𝑓′(𝑥)=lím𝑥→1−⁡𝑒𝑥=𝑒,𝑓′+(1)=lím𝑥→1+⁡𝑓′(𝑥)=lím𝑥→1+⁡(2𝑥+𝑒)=2+𝑒. Observamos que 𝑓′−(1) ≠𝑓′+(1), así que 𝑓 no es derivable en 𝑥 =1.
  2. La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =0 viene dada por: 𝑦−𝑓(0)=𝑓′(0)(𝑥−0)⇔𝑦−4=𝑥⇔𝑦=𝑥+4.
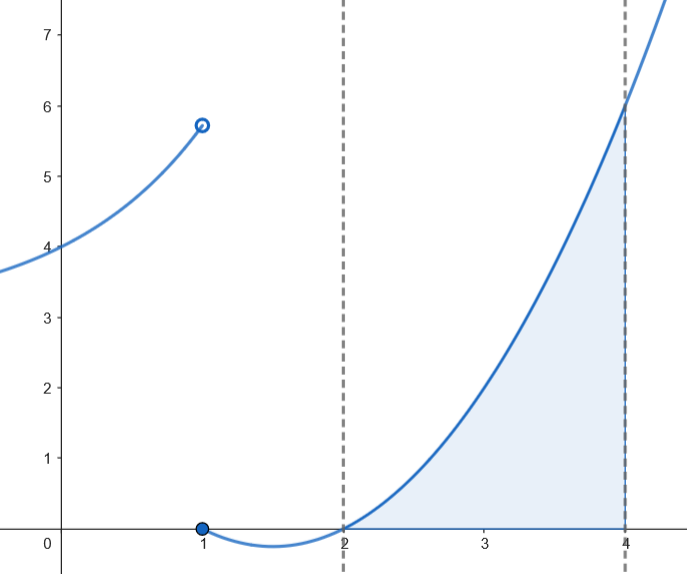  3. Si 𝑎 = −3, la función no es continua en 𝑥 =1 por el apartado anterior. Observamos que la segunda rama es una parábola con vértice (32,−14). Representamos la región. Figura Calculamos el área. ∫42𝑓(𝑥)𝑑𝑥=∫42(𝑥2−3𝑥+2)𝑑𝑥=[13𝑥3−32𝑥2+2𝑥]42=643−24+8−(83−6+4)=143𝑢2.

Ejercicio 5

Una tienda vende ropa de tallas M, L y XL. Se sabe que el 65% de sus clientes son mujeres. El 50% de las mujeres que compran ropa en esa tienda usan la talla M y el 10% la talla XL. De los hombres, el 40% usan la talla L y el 45% la XL.

  1. ¿Qué porcentaje de mujeres que compran ropa en esa tienda no usan la talla XL?
  2. Halle el porcentaje de clientes que no usan la talla L.
  3. De los clientes que usan la talla M, ¿qué porcentaje son mujeres?

Resolución

Llamamos 𝑊 a ser mujer, 𝐻 a ser hombre, 𝑀 a usar la talla M, 𝐿 a usar la talla L y 𝑋 a usar la talla XL. Podemos hacer un diagrama de árbol.

𝑀
0,5←←←←←←←←←←→
𝑊 0,4←←←←←←←←←←→ 𝐿
0,65←←←←←←←←←←←→ 0,1←←←←←←←←←←→
𝑋
𝑀
0,35←←←←←←←←←←←→ 0,15←←←←←←←←←←←→
𝐻 0,4←←←←←←←←←←→ 𝐿
0,45←←←←←←←←←←←→
𝑋
  1. La probabilidad de que un cliente no use la talla XL sabiendo que es mujer es: 𝑃(𝑋𝑐|𝑊)=1−𝑃(𝑋|𝑊)=1−0,1=0,9. Por tanto, el 90% de las mujeres que compran ropa en esa tienda no usan la talla XL.
  2. Por el teorema de la probabilidad total, la probabilidad de que un cliente use la talla L es: 𝑃(𝐿)=𝑃(𝐿∩𝑊)+𝑃(𝐿∩𝐻)=𝑃(𝑊)⋅𝑃(𝐿|𝑊)+𝑃(𝐻)⋅𝑃(𝐿|𝐻)=0,65⋅0,4+0,35⋅0,4=0,4. Así que la probabilidad de que un cliente no use la talla L es: 𝑃(𝐿𝑐)=1−𝑃(𝐿)=1−0,4=0,6. Por tanto, el 60% de los clientes no usan la talla L.
  3. Por el teorema de la probabilidad total, la probabilidad de que un cliente use la talla M es: 𝑃(𝑀)=𝑃(𝑀∩𝑊)+𝑃(𝑀∩𝐻)=𝑃(𝑊)⋅𝑃(𝑀|𝑊)+𝑃(𝐻)⋅𝑃(𝑀|𝐻)=0,65⋅0,5+0,35⋅0,15=0,3775. La probabilidad de que un cliente sea mujer sabiendo que usa la talla M es: 𝑃(𝑊|𝑀)=𝑃(𝑊∩𝑀)𝑃(𝑀)=𝑃(𝑊)⋅𝑃(𝑀|𝑊)𝑃(𝑀)=0,65⋅0,50,3775≈0,8609. Por tanto, el 86,09% de los clientes que usan la talla M son mujeres.

Ejercicio 6

El 75% de los estudiantes de un centro aprueba la asignatura A y un 55% aprueba la asignatura B. Además, un 35% del total de estudiantes aprueba ambas. Elegido un estudiante al azar de este centro, calcule las siguientes probabilidades:

  1. No apruebe B sabiendo que ha aprobado A.
  2. Aprueba alguna de estas asignaturas.
  3. No apruebe ni A ni B.
  4. Haya aprobado A si se sabe que ha aprobado alguna de estas dos asignaturas.
  5. Estudie si los sucesos "aprobar A" y "aprobar B" son independientes.

Resolución

Llamamos 𝐴 a aprobar la asignatura A y 𝐵 a aprobar la asignatura B. Sabemos que: 𝑃(𝐴)=0,75,𝑃(𝐵)=0,55y𝑃(𝐴∩𝐵)=0,35.

  1. La probabilidad de que no apruebe B sabiendo que ha aprobado A es: 𝑃(𝐵𝑐|𝐴)=1−𝑃(𝐵|𝐴)=1−𝑃(𝐵∩𝐴)𝑃(𝐴)=1−0,350,75≈0,5333.
  2. La probabilidad de que apruebe alguna de estas asignaturas es: 𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵)=0,75+0,55−0,35=0,95.
  3. La probabilidad de que no apruebe ni A ni B es: 𝑃(𝐴𝑐∩𝐵𝑐)=𝑃((𝐴∪𝐵)𝑐)=1−𝑃(𝐴∪𝐵)=1−0,95=0,05.
  4. La probabilidad de que haya aprobado A sabiendo que ha aprobado alguna de estas asignaturas es: 𝑃(𝐴|𝐴∪𝐵)=𝑃(𝐴)𝑃(𝐴∪𝐵)=0,750,95≈0,7895.
  5. Como 𝑃(𝐵𝑐|𝐴) ≠𝑃(𝐵𝑐), los sucesos 𝐴 y 𝐵 no son independientes.

Ejercicio 7

  1. Para estimar la proporción de mujeres matriculadas en carreras STEM en Andalucía, se realiza una encuesta a 2.000 universitarias andaluzas elegidas al azar y se obtiene que 710 de ellas están matriculadas en carreras STEM. Con un nivel de confianza del 96,5%, calcule un intervalo de confianza para estimar la proporción de mujeres matriculadas en carreras STEM en Andalucía.
  2. En otra comunidad autónoma, al seleccionar una muestra de universitarias, se observa que el porcentaje de mujeres matriculadas en carreras STEM es del 37%. Con un nivel de confianza del 98%, calcule el tamaño mínimo de esa nueva muestra para que el error máximo cometido sea del 1,5%.

Resolución
  1. Como 710 universitarias de 𝑛 =2.000 están matriculadas en carreras STEM, la proporción muestral es: 𝑝=7102.000=0,355. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 96,5%, entonces: 𝛼=1−0,965=0,035⇒1−𝛼2=1−0,0352=0,9825⇒𝑧𝛼/2=2,11. Por tanto, el intervalo de confianza para estimar la proporción de universitarias que están matriculadas en carreras STEM con un nivel de confianza del 96,5% es: 𝐼=(0,355−2,11⋅√0,355⋅(1−0,355)2.000,0,355+2,11⋅√0,355⋅(1−0,355)2.000)≈(0,3324;0,3776).
  2. La proporción muestral es 𝑝 =0,37. Si además el nivel de confianza es del 98%, entonces: 𝛼=1−0,90=0,02⇒1−𝛼2=1−0,022=0,99⇒𝑧𝛼/2=2,33. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=2,33⋅√0,37⋅(1−0,37)𝑛=2,33⋅√0,2331𝑛. Si se quiere el error máximo sea de 0,015, entonces: 2,33⋅√0,2331𝑛=0,015⇔√0,2331𝑛=0,0152,33⇔0,2331𝑛=0,01522,332⇔𝑛=0,2331⋅2,3320,0152=5.624,3404. Por tanto, el número mínimo de personas de la muestra debe ser 5.625.

Ejercicio 8

La cuota mensual de las hipotecas en una ciudad es una variable aleatoria que sigue una distribución Normal de media desconocida y desviación típica igual a 140€.

  1. Se toma una muestra aleatoria de hipotecas en dicha ciudad y se obtiene que el intervalo de confianza al 95% para la media de las cuotas mensuales es (517,65; 551,95). Calcule el valor de la media muestral y el tamaño de la muestra elegida.
  2. Escogida otra muestra de 78 hipotecas en esa ciudad y con un nivel de confianza del 97%, calcule el error máximo cometido para estimar la cuota mensual media.
  3. Si en otra ciudad la cuota mensual de las hipotecas sigue una distribución Normal de media 540€ y desviación típica de 150€, calcule la probabilidad de que la cuota de una hipoteca elegida al azar en dicha ciudad esté comprendida entre 600 y 700 euros.

Resolución
  1. En primer lugar, la media muestral viene dada por el punto medio del intervalo. ――𝑥=517,65+551,952=534,8. Por otro lado, el error cometido viene dado por la mitad de la amplitud del intervalo. 𝐸=551,95−517,652=17,15. Como el nivel de confianza es del 95%, entonces: 𝛼=1−0,95=0,05⇒1−𝛼2=1−0,052=0,975⇒𝑧𝛼/2=1,96. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=1,96⋅140√𝑛=274,4√𝑛. Como el error cometido es 17,15, se tiene que verificar: 274,4√𝑛=17,15⇔√𝑛=274,417,15⇔𝑛=(274,417,15)2=256. Por tanto, el tamaño de la muestra es 256.
  2. Si el nivel de confianza es del 97%, entonces 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=2,17⋅140√78≈34,3986.
  3. La cuota mensual de las hipotecas 𝑋 sigue una distribución 𝑁(540,150). La probabilidad de que la cuota de una hipoteca esté comprendida entre 600 y 700 euros es: 𝑃(600≤𝑋≤700)=𝑃(600−540150≤𝑍≤700−540150)=𝑃(0,4<𝑍<1,07)==𝑃(𝑍<1,07)−𝑃(𝑍<0,4)=0,8577−0,6554=0,2023.