Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 1 de 2022

Ejercicio 1

Considere la matriz 𝐴=⎛⎜ ⎜ ⎜⎝2−3−𝑎−1−1𝑎𝑎+11−3−𝑎⎞⎟ ⎟ ⎟⎠, donde 𝑎 es un número real. Determine de manera justificada:

  1. Los valores de 𝑎 para los que la matriz 𝐴 tiene inversa.
  2. Las matrices 𝐴2, 𝐴3 y 𝐴2022 para 𝑎 =4.
  3. La matriz 𝑋 que verifica que 𝑋𝐴 =𝐼3 para 𝑎 =3.

Resolución
  1. Calculamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣2−3−𝑎−1−1𝑎𝑎+11−3−𝑎∣=−2𝑎2−3(𝑎+1)−3(𝑎+1)+𝑎(𝑎+1)+3𝑎+6(𝑎+1)=−𝑎2+4𝑎. La inversa de 𝐴 existe si y solo si su determinante es no nulo. |𝐴|=0⇔−𝑎2+4𝑎=0⇔𝑎(−𝑎+4)=0⇔{𝑎=0,−𝑎+4=0⇔𝑎=4. Por tanto, la matriz 𝐴 tiene inversa si 𝑎 ≠0 y 𝑎 ≠4.
  2. Si 𝑎 =4, 𝐴=⎛⎜ ⎜ ⎜⎝2−3−5−1451−3−4⎞⎟ ⎟ ⎟⎠. Calculamos la matriz 𝐴2. 𝐴2=𝐴⋅𝐴=⎛⎜ ⎜ ⎜⎝2−3−5−1451−3−4⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝2−3−5−1451−3−4⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝2−3−5−1451−3−4⎞⎟ ⎟ ⎟⎠=𝐴. Como 𝐴2 =𝐴, 𝐴3=𝐴2⋅𝐴=𝐴⋅𝐴=𝐴. En general, 𝐴𝑛 =𝐴. Por tanto, 𝐴2022=𝐴=⎛⎜ ⎜ ⎜⎝2−3−5−1451−3−4⎞⎟ ⎟ ⎟⎠.
  3. Si 𝑎 =3, por el primer apartado 𝐴 es invertible y det(𝐴) =3. Resolvemos la ecuación matricial. 𝑋𝐴=𝐼3⇔𝑋=𝐴−1. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝3103−230−43⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=13⎛⎜ ⎜ ⎜⎝3301−2−4033⎞⎟ ⎟ ⎟⎠. Por tanto, 𝑋=𝐴−1=13⎛⎜ ⎜ ⎜⎝3301−2−4033⎞⎟ ⎟ ⎟⎠.

Ejercicio 2

Una sastrería dispone de 70 m2 de tela de lino y de 150 m2 de tela de algodón. En la confección de un traje se emplea 1 m2 de tela de lino y 3 m2 de tela de algodón, y en un vestido se necesitan 2 m2 de tela de cada tipo. Se obtienen 60 euros de beneficio por cada traje y 70 euros por cada vestido. Determine el número de trajes y vestidos que se deben confeccionar para obtener el máximo beneficio, así como dicho beneficio máximo.

Resolución

Llamamos 𝑥 al número de trajes e 𝑦 al número de vestidos. Podemos organizar la información en una tabla.

Lino (m2) Algodón (m2) Beneficios (€)
Traje 1 3 60
Vestido 2 2 70
Total 70 150

Las restricciones del problema son: ⎧{ { {⎨{ { {⎩𝑥+2𝑦≤70,3𝑥+2𝑦≤150,𝑥≥0,𝑦≥0. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=60𝑥+70𝑦.

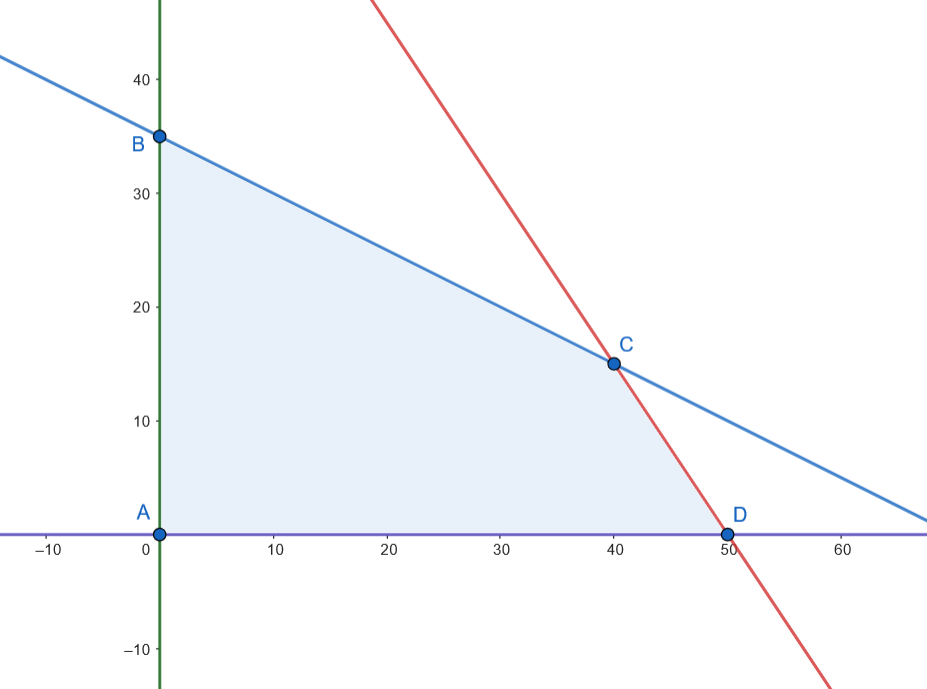Representamos la región factible. Figura Los vértices son: 𝐴(0,0),𝐵(0,35),𝐶(40,15)y𝐷(50,0).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(0,0)=0,𝐹(𝐵)=𝐹(0,35)=2.450,𝐹(𝐶)=𝐹(40,15)=3.450,𝐹(𝐷)=𝐹(50,0)=3.000. Por tanto, el valor máximo de los beneficios se alcanza confeccionando 40 trajes y 15 vestidos, con unas ganancias de 3.450€.

Ejercicio 3

Se considera la función 𝑓(𝑥)=⎧{ {⎨{ {⎩𝑎(𝑥+1)2,si −3≤𝑥≤1,𝑏𝑥22+2,si 1<𝑥≤2, con 𝑎 y 𝑏 números reales.

  1. Determine los valores de 𝑎 y 𝑏 para que 𝑓 sea continua y derivable.
  2. Para 𝑎 =1 y 𝑏 =2, esboce la gráfica de la función 𝑓 y calcule el área del recinto limitado por la gráfica de 𝑓, el eje 𝑂𝑋 y las rectas 𝑥 = −2 y 𝑥 =1.

Resolución
    • Si 𝑥 ∈[ −3,2] con 𝑥 ≠1, 𝑓 es continua y derivable con 𝑓′(𝑥)={2𝑎(𝑥+1),si −3≤𝑥<1,𝑏𝑥,si 1<𝑥≤2.
    • Estudiamos la continuidad para el punto de ruptura 𝑥 =1. lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡𝑎(𝑥+1)2=4𝑎,lím𝑥→1+⁡𝑓(𝑥)=lím𝑥→1+⁡(𝑏𝑥22+2)=𝑏2+2,𝑓(1)=4𝑎. Para que 𝑓 sea continua, ha de verificarse 4𝑎=𝑏2+2⇔8𝑎=𝑏+4. Pasamos a estudiar la derivabilidad. 𝑓′−(1)=lím𝑥→1−⁡𝑓′(𝑥)=lím𝑥→1−⁡2𝑎(𝑥+1)=4𝑎,𝑓′+(1)=lím𝑥→1+⁡𝑓′(𝑥)=lím𝑥→1+⁡𝑏𝑥=𝑏. Para que 𝑓 sea derivable, ha de verificarse 4𝑎=𝑏.
    Con estas dos condiciones, planteamos el sistema de ecuaciones {8𝑎=𝑏+4,4𝑎=𝑏. Resolvemos el sistema por reducción. Si restamos las ecuaciones, obtenemos que 4𝑎=4⇔𝑎=1. Sustituyendo en la segunda ecuación, 𝑏=4𝑎𝑎=1←←←←←←→𝑏=4. Por tanto, 𝑎 =1 y 𝑏 =4.
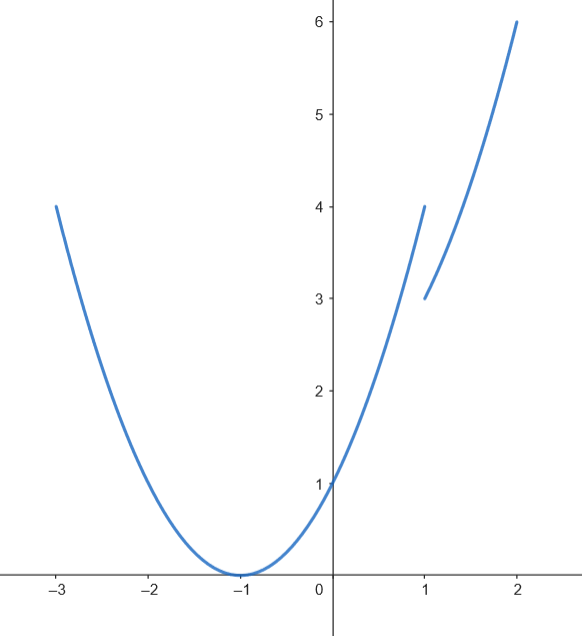  2. Si 𝑎 =1 y 𝑏 =2, por el apartado anterior 𝑓 no es continua en 𝑥 =1. Representamos gráficamente la función. Observamos que la primera rama es una parábola con vértice ( −1,0). Figura Podemos representar gráficamente el recinto acotado limitado por la gráfica de 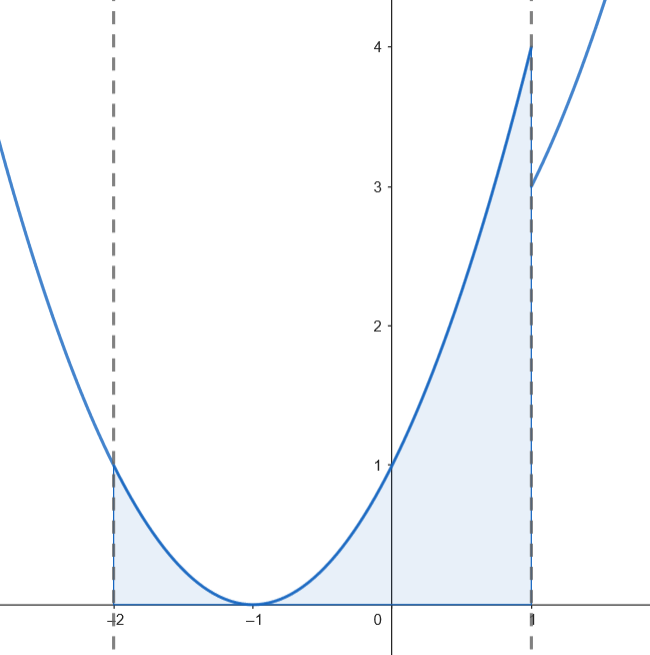𝑓, el eje 𝑋 y las rectas 𝑥 = −2 y 𝑥 =1. Figura Calculamos el área. ∫1−2𝑓(𝑥)𝑑𝑥=∫1−2(𝑥+1)2𝑑𝑥=∫1−2(𝑥2+2𝑥+1)𝑑𝑥=[13𝑥3+𝑥2+𝑥]1−2==13+1+1−(−83+4−2)=3𝑢2.

Ejercicio 4

Se considera la función 𝑓(𝑥)=𝑥−3𝑥+2.

  1. Determine el dominio de la función y estudie su monotonía y curvatura.
  2. Calcule las ecuaciones de las asíntotas de 𝑓 si existen. Calcule los puntos de corte de la gráfica de 𝑓 con los ejes de coordenadas.
  3. Represente la gráfica de la función 𝑓.

Resolución
    • La función 𝑓 es una función racional, así que los puntos que no pertenecen al dominio son aquellos que anulan al denominador. 𝑥+2=0⇔𝑥=−2. Por tanto, Dom⁡(𝑓) =ℝ ∖{ −2}.
    • Estudiamos la monotonía. En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=𝑥+2−(𝑥−3)(𝑥+2)2=5(𝑥+2)2. Observamos que 𝑓′(𝑥) >0 para 𝑥 ≠ −2, así que 𝑓 es creciente en todo su dominio y no tiene extremos.
    • Estudiamos la curvatura. Para ello, calculamos la segunda derivada de 𝑓. 𝑓″(𝑥)=−10(𝑥+2)3. Observamos que 𝑓″(𝑥) ≠0 para 𝑥 ≠ −2, así que no tiene puntos de inflexión. Estudiamos el signo de la segunda derivada, considerando 𝑥 = −2 por no pertenecer al dominio.
      ( −∞, −2) ( −2, +∞)
      signo de 𝑓″ + −
      curvatura de 𝑓 ⌣ ⌢
      Por tanto, la función es convexa en ( −∞,2) y cóncava en (2, +∞).
    • El denominador se anula en 𝑥 = −2 y observamos que lím𝑥→−2−⁡𝑓(𝑥)=lím𝑥→−2−⁡𝑥−3𝑥+2=+∞,lím𝑥→−2+⁡𝑓(𝑥)=lím𝑥→−2+⁡𝑥−3𝑥+2=−∞. Por tanto, la recta 𝑥 = −2 es una asíntota vertical.
    • Veamos si tiene una asíntota horizontal. lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡𝑥−3𝑥+2=1. Por tanto, la recta 𝑦 =1 es una asíntota horizontal.
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑓(𝑥)=0⇔𝑥−3𝑥+2=0⇔𝑥−3=0⇔𝑥=3. Luego el único punto de corte con el eje 𝑋 es (3,0).
    • Hallamos ahora el punto de corte con el eje 𝑌. 𝑓(0)=−32. Así que el punto de corte con el eje 𝑌 es (0,−32).
  3. Representamos gráficamente la función usando la información de los apartados anteriores. Figura

Ejercicio 5

El 80% de los restaurantes de una localidad admite el pago con tarjeta de crédito, el 50% admite pagar mediante el móvil y el 10% no admite el pago con ninguno de estos métodos. Escogido al azar un restaurante de dicha localidad.

  1. Calcule la probabilidad de que el restaurante admita:
    1. Alguno de estos dos medios de pago.
    2. Pagar con móvil sabiendo que admite pagar con tarjeta de crédito.
  2. ¿Son independientes los sucesos "Pagar con tarjeta" y "Pagar con móvil"?

Resolución

Llamamos 𝑇 a admitir el pago con tarjeta de crédito y 𝑀 a admitir el pago mediante el móvil. Sabemos que: 𝑃(𝑇)=0,8,𝑃(𝑀)=0,5y𝑃(𝑇𝑐∩𝑀𝑐)=0,1.

    1. La probabilidad de que el restaurante admita uno de los dos medios de pago es: 𝑃(𝑇∪𝑀)=1−𝑃((𝑇∪𝑀)𝑐)=1−𝑃(𝑇𝑐∩𝑀𝑐)=1−0,1=0,9.
    2. La probabilidad de admitir uno de los dos medios de pago viene dada por: 𝑃(𝑇∪𝑀)=𝑃(𝑇)+𝑃(𝑀)−𝑃(𝑇∩𝑀). Así que, despejando en la expresión anterior, la probabilidad de admitir los dos medios de pago es: 𝑃(𝑇∩𝑀)=𝑃(𝑇)+𝑃(𝑀)−𝑃(𝑇∪𝑀)=0,8+0,5−0,9=0,4. Por tanto, la probabilidad de que admita pagar con móvil sabiendo que admite pagar con tarjeta es: 𝑃(𝑀|𝑇)=𝑃(𝑀∩𝑇)𝑃(𝑇)=0,40,8=0,5.
  2. Como 𝑃(𝑀) =𝑃(𝑀|𝑇), los sucesos 𝑇 y 𝑀 son independientes.

Ejercicio 6

En una localidad se han vendido 1.335 boletos de lotería en tres establecimientos A, B y C. En el establecimiento A se han vendido 1.054 boletos, 99 en B y el resto en C. De los boletos premiados, 5 han sido vendidos en B y 13 en C. Sabemos que 95 de cada 100 boletos vendidos no han obtenido premio. Elegido un boleto al azar, se pide:

  1. ¿Cuál es el establecimiento que tiene una mayor probabilidad de haber vendido un boleto no premiado?
  2. ¿Cuál es la probabilidad de que un boleto no premiado haya sido vendido en el establecimiento A?

Resolución

Llamamos 𝐴 a ser vendido en el establecimiento A, 𝐵 en el establecimiento B, 𝐶 en el establecimiento C y 𝐺 a obtener un premio. Podemos hacer un diagrama de árbol.

𝐺
𝑝←←←←←←←←←→
𝐴
1054/1335←←←←←←←←←←←←←←←←←→ 1−𝑝←←←←←←←←←←←→
𝐺𝑐
𝐺
5/99←←←←←←←←←←←←→
99/1335←←←←←←←←←←←←←←←→ 𝐵
94/99←←←←←←←←←←←←←→
𝐺𝑐
𝐺
182/1335←←←←←←←←←←←←←←←←→ 13/182←←←←←←←←←←←←←←→
𝐶
169/182←←←←←←←←←←←←←←←→
𝐺𝑐

También sabemos que: 𝑃(𝐺𝑐)=0,95⇒𝑃(𝐺)=0,05.

  1. Por el teorema de la probabilidad total, la probabilidad de obtener un boleto premiado viene dada por: 𝑃(𝐺)=𝑃(𝐴)⋅𝑃(𝐺|𝐴)+𝑃(𝐵)⋅𝑃(𝐺|𝐵)+𝑃(𝐶)⋅𝑃(𝐺|𝐶)=10541335⋅𝑝+991335⋅599+1821335⋅13182==10541335𝑝+51335+131335=1054𝑝+181335. Como 𝑃(𝐺) =0,05, 1054𝑝+181335=0,05⇔1054𝑝+18=66,75⇔1054𝑝=48,75⇔𝑝=48,751054≈0,0463. Así que la probabilidad de vender un boleto no premiado en 𝐴 es: 𝑃(𝐺𝑐|𝐴)=1−𝑃(𝐺|𝐴)=1−0,0463=0,9537. Observamos que: 𝑃(𝐺𝑐|𝐴)=0,9537,𝑃(𝐺𝑐|𝐵)=9499≈0,9495y𝑃(𝐺𝑐|𝐶)=169182≈0,9286. Por tanto, el establecimiento A es el que tiene una mayor probabilidad de haber vendido un boleto no premiado.
  2. La probabilidad de que un boleto no premiado haya sido vendido en el establecimiento A es: 𝑃(𝐴|𝐺𝑐)=𝑃(𝐴∩𝐺𝑐)𝑃(𝐺𝑐)=𝑃(𝐴)⋅𝑃(𝐺𝑐|𝐴)𝑃(𝐺𝑐)=10541335⋅0,95370,95≈0,7926.

Ejercicio 7

  1. Se divide una población en cuatro estratos de tamaño 60.000, 20.000, 24.000 y 16.000 personas. En dicha población se realiza un muestreo estratificado por afijación proporcional, seleccionándose 144 personas del tercer estrato. Determine el tamaño total de la muestra y su composición.
  2. Dada la población {1,4,7}, establezca todas las muestras posibles de tamaño 2 que se puedan formar mediante muestreo aleatorio simple y determinar la media y la desviación típica de las medias muestrales obtenidas con todas estas muestras.

Resolución
  1. Llamamos 𝑥 al número de individuos en la muestra del primer estrato, 𝑦 en la muestra del segundo estrato y 𝑧 en la muestra del cuarto estrato. Como se usa afijación proporcional y se seleccionan 144 individuos del tercer estrato, 60.000𝑥=20.000𝑦=24.000144=16.000𝑧. Despejamos estos valores. 24.000144=60.000𝑥⇔𝑥=144⋅60.00024.000=360,24.000144=20.000𝑦⇔𝑦=144⋅20.00024.000=120,24.000144=16.000𝑧⇔𝑧=144⋅16.00024.000=96. Por tanto, la muestra está compuesta por 360 individuos del primer estrato, 120 del segundo estrato, 144 del tercer estrato y 96 del cuarto estrato. Así que el tamaño de la muestra es 360+120+144+96=720.
  2. Las muestras posibles de tamaño 2 son (1,1)(1,4)(1,7)(4,1)(4,4)(4,7)(7,1)(7,4)(7,7). Hallamos la media 𝜇 y la varianza 𝜎2 de la población. 𝜇=1+4+73=4,𝜎2=(1−4)2+(4−4)2+(7−4)23=6. Por tanto, la distribución de medias muestrales de tamaño 2 tiene media 𝜇 =4 y desviación típica 𝜎√2=√6√2=√3.

Ejercicio 8

Se desea estimar la proporción de estudiantes de una universidad que proceden de otras provincias, para ello se selecciona una muestra de tamaño 2.100 de los que 630 lo cumplen.

  1. Calcule un intervalo de confianza con un nivel del 97,5% para estimar la proporción poblacional de estudiantes de esa universidad procedentes de otras provincias.
  2. En una nueva muestra que mantiene la misma proporción muestral, y con el mismo nivel de confianza, queremos que el error máximo cometido sea de 0,01. Halle su tamaño mínimo.

Resolución
  1. Como 630 estudiantes de 𝑛 =2.100 provienen de otras provincias, la proporción muestral es: 𝑝=6302.100=0,3. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 97,5%, entonces: 𝛼=1−0,975=0,025⇒1−𝛼2=1−0,0252=0,9875⇒𝑧𝛼/2=2,24. Por tanto, el intervalo de confianza para estimar la proporción poblacional de estudiantes que proceden de otras provincias con un nivel de confianza del 97,5% es: 𝐼=(0,3−2,24⋅√0,3⋅(1−0,3)2.100,0,3+2,24⋅√0,3⋅(1−0,3)2.100)=(0,2776;0,3224).
  2. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=2,24⋅√0,3⋅(1−0,3)𝑛=2,24⋅√0,21√𝑛. Si se quiere que el error máximo sea de 0,01, entonces: 2,24⋅√0,21√𝑛=0,01⇔√𝑛=2,24⋅√0,210,01⇔𝑛=2,242⋅0,210,012=10.536,96. Por tanto, el tamaño mínimo de la muestra debe ser de 10.537 estudiantes.