Icono Matemáticas de Selectividad

Buscar GitHub

📋 Junio de 2025

Ejercicio 1

  1. Plantee y resuelva el siguiente problema de forma matricial: El gerente de una empresa de productos hospitalarios desea introducir un nuevo producto en el mercado nacional. Para ello contrata a 3 vendedores que se han encargado de las zonas A, B y C del país, respectivamente. El vendedor de la zona A ha trabajado 40 horas, ha realizado 10 demostraciones y 5 viajes para dicha promoción. El vendedor de la zona B ha trabajado el doble de horas que el de la zona A, realizando 15 demostraciones y 8 viajes. En cuanto al vendedor de la zona C, ha trabajado 100 horas, ha realizado 25 demostraciones y 10 viajes. El gerente debe abonarles 75€ por hora trabajada, 300€ por demostración y 250€ por viaje realizado. Teniendo en cuenta que, además, debe aplicárseles una retención en concepto del impuesto del IRPF del 15% si la cantidad a abonar al vendedor es menor de diez mil euros y del 18% en caso contrario, determine la cantidad final que cobrará cada vendedor.
  2. Sea 𝐴=⎛⎜ ⎜ ⎜⎝−2213𝑎−12403⎞⎟ ⎟ ⎟⎠. ¿Para qué valores de 𝑎 es la matriz 𝐴 invertible?

Resolución
  1. Podemos recoger la información en las matrices: 𝐴=⎛⎜ ⎜ ⎜⎝40105801581002510⎞⎟ ⎟ ⎟⎠,𝐵=⎛⎜ ⎜ ⎜⎝75300250⎞⎟ ⎟ ⎟⎠.
    • La matriz 𝐴 recoge los números de horas trabajadas, demostraciones y viajes por cada vendedor. Las filas indican los vendedores y las columnas las horas trabajadas, demostraciones y viajes, respectivamente.
    • La matriz 𝐵 recoge la cantidad que debe ser abonada por cada hora trabajada, demostración y viaje, respectivamente.
    Así que la cantidad de dinero sin aplicar impuestos que recibe cada vendedor en euros viene dada por el producto: 𝐶=𝐴⋅𝐵=⎛⎜ ⎜ ⎜⎝40105801581002510⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝75300250⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝7.25012.50017.500⎞⎟ ⎟ ⎟⎠. Como la cantidad a abonar a los vendedores de las zonas B y C es superior a 10.000€, la matriz que recoge el porcentaje que cobra cada vendedor al aplicar la retención del IRPF es: 𝐷=(0,850,820,82). Por tanto, la cantidad final que cobra cada vendedor viene dada por la diagonal del producto: 𝐶⋅𝐷=⎛⎜ ⎜ ⎜⎝7.25012.50017.500⎞⎟ ⎟ ⎟⎠(0,850,820,82)=⎛⎜ ⎜ ⎜⎝6.162,55.9455.94510.62510.25010.25014.87514.35014.350⎞⎟ ⎟ ⎟⎠. Es decir, los vendedores de las zonas A, B y C cobran 6.162,5€, 10.250€ y 14.350€, respectivamente.
  2. Calculamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣−2213𝑎−12403∣=−6(𝑎−1)+16−4(𝑎−1)−18=−10𝑎+8. La inversa de 𝐴 existe cuando su determinante es no nulo. |𝐴|=0⇔−10𝑎+8=0⇔10𝑎=8⇔𝑎=45. Por tanto, la matriz es invertible si 𝑎 ≠45.

Ejercicio 2

Un periódico digital ha publicado una noticia de última hora. El número de personas que han visto la noticia 𝑡 horas después de su lanzamiento viene modelado por la función: 𝑁(𝑡)=500.000⋅(1−𝑒−0,2𝑡),𝑡>0.

  1. Estudie la monotonía y curvatura de la función 𝑁.
  2. Represente gráficamente la función 𝑁 y describa su tendencia a lo largo del tiempo.
  3. ¿Cuánto tiempo ha debido de pasar para que la noticia haya sido vista por 450.000 personas?
  4. La velocidad de difusión de la noticia (número de personas por hora que han visto la publicación) es 𝑁′(𝑡). ¿Qué conclusión se obtiene al comparar 𝑁′(𝑡) en los instantes 𝑡 =1 y 𝑡 =10?

Resolución
  1. En primer lugar, hallamos las dos primeras derivadas de la función 𝑁. 𝑁′(𝑡)=500.000⋅(−𝑒−0,2𝑡)⋅(−0,2)=100.000𝑒−0,2𝑡,𝑁″(𝑡)=100.000𝑒−0,2𝑡⋅(−0,2)=−20.000𝑒−0,2𝑡.
    • Observamos que 𝑁′(𝑡) >0 para 𝑡 >0, así que 𝑁 es creciente en todo su dominio.
    • Observamos que 𝑁″(𝑡) <0 para 𝑡 >0, así que 𝑁 es cóncava en todo su dominio.
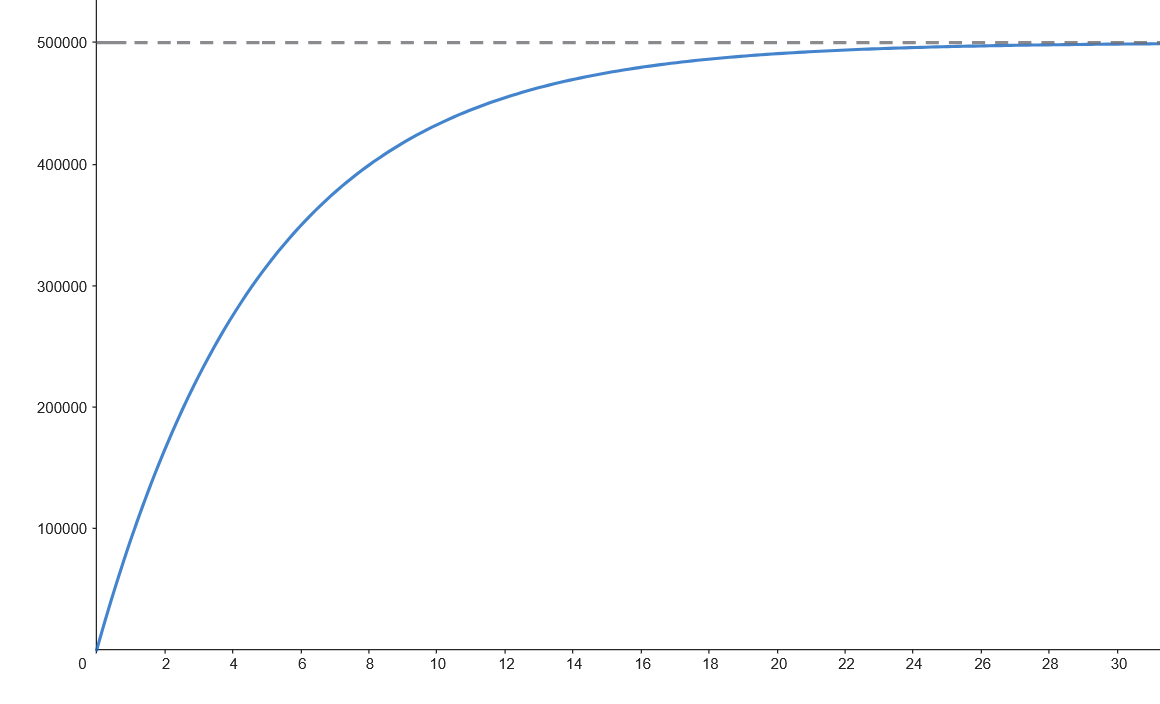  2. Veamos si la gráfica de la función tiene asíntota horizontal para estudiar su tendencia. lím𝑡→+∞⁡𝑁(𝑡)=lím𝑡→+∞⁡500.000(1−𝑒−0,2𝑡)=500.000. Por tanto, la recta 𝑦 =500.000 es una asíntota horizontal. Representamos gráficamente la función usando esta información. Figura Podemos observar que el número de personas que ven la noticia aumenta rápidamente en las primeras horas y se va acercando a 500.000, cada vez con menor velocidad.
  3. Para que la noticia haya sido vista por 450.000 personas ha de verificarse que: 𝑁(𝑡)=450.000⇔500.000(1−𝑒−0,2𝑡)=450.000⇔1−𝑒−0,2𝑡=910⇔𝑒−0,2𝑡=110⇔⇔−0,2𝑡=ln⁡(110)⇔𝑡=−ln⁡(110)0,2=5ln⁡(10)≈11,5129. Por tanto, han debido de pasar un poco más de 11 horas y media.
  4. Calculamos el valor de la derivada en los dos instantes. 𝑁′(1)≈81.873,0753,𝑁′(10)≈13.533,5283. Observamos que la velocidad de difusión de la noticia se reduce en gran medida con el paso de las horas.

Ejercicio 3

A un paciente con diabetes se le monitoriza durante un día completo, suministrándole un medicamento a mediodía para observar su reacción. La cantidad de glucosa en sangre (mg/dl) del paciente, en cada instante 𝑡 (horas), es: 𝑓(𝑡)=⎧{ {⎨{ {⎩56(𝑡33−12𝑡2+108𝑡+108),si 0≤𝑡≤12,𝑡2−40𝑡+546,si 12<𝑡≤24.

  1. Halle en qué periodos de tiempo el nivel de glucosa va aumentando.
  2. ¿En qué momentos del día el paciente tiene los niveles más alto y más bajo de glucosa en sangre y a cuánto ascienden?
  3. ¿En qué momentos, después del mediodía, el paciente tiene 155 mg/dl?

Resolución
  1. Si 𝑡 ≠12, la función es continua y derivable con: 𝑓′(𝑡)={56(𝑡2−24𝑡+108),si 0≤𝑡<12,2𝑡−40,si 12<𝑡≤24. Para hallar los puntos críticos, igualamos las dos ramas de la derivada a cero.
    • Si 0 <𝑡 <12, 𝑓′(𝑡)=0⇔56(𝑡2−24𝑡+108)=0⇔𝑡2−24𝑡+108=0⇔{𝑡=6,𝑡=18∉(0,12).
    • Si 12 <𝑡 <24, 𝑓′(𝑡)=0⇔2𝑡−40=0⇔2𝑡=40⇔𝑡=20.
    Así que los puntos críticos son 𝑡 =6 y 𝑡 =20. También consideramos 𝑡 =12 por ser el punto de ruptura. Estudiamos el signo de la derivada.
    (0,6) (6,12) (12,20) (20,24)
    signo de 𝑓′ + − − +
    monotonía de 𝑓 → → → →
    Por tanto, 𝑓 es creciente en (0,6) y (20,24). Es decir, la glucosa aumenta a lo largo de las seis primeras horas y a partir de las 20 horas.
  2. Los puntos (6,330) y (24,162) son máximos relativos y los puntos (0,90) y (20,146) son mínimos relativos. Por tanto, (6,330) es el máximo absoluto y (0,90) es el mínimo absoluto. Es decir, el nivel más alto se alcanza a las seis horas, con 330 mg/dl, y el nivel más bajo lo tiene al principio del día, con 90 mg/dl.
  3. Si 𝑡 >6, 𝑓(𝑡)=155⇔𝑡2−40𝑡+546=155⇔𝑡2−40𝑡+391=0⇔{𝑡=17,𝑡=23. Por tanto, el paciente alcanza una cantidad de glucosa de 155 mg/dl a las 17 horas y a las 23 horas.

Ejercicio 4

En una casa con trastero viven tres personas y cada una tiene un llavero con las llaves de la casa. El primer llavero contiene 7 llaves, el segundo 8 y el tercero 5. En cada uno de los llaveros hay una única llave que abre el trastero. Otra persona necesita abrir el trastero y, para ello, selecciona un llavero al azar y, de este, elige una llave aleatoriamente e intenta abrirlo. Calcule la probabilidad de que:

  1. No haya acertado con la llave seleccionada.
  2. El llavero sea el tercero y la llave abra el trastero.
  3. Sabiendo que la llave elegida abre el trastero, esta pertenezca al primer o al tercer llavero.
  4. Si la llave no abre el trastero, esta no pertenezca al primer llavero.

Resolución

Llamamos 𝐿1 a seleccionar el llavero 1, 𝐿2 a seleccionar el llavero 2, 𝐿3 a seleccionar el llavero 3 y 𝐴 a abrir el trastero. Podemos hacer un diagrama de árbol.

𝐴
1/7←←←←←←←←←←←→
𝐿1
1/3←←←←←←←←←←←→ 6/7←←←←←←←←←←←→
𝐴𝑐
𝐴
1/8←←←←←←←←←←←→
1/3←←←←←←←←←←←→ 𝐿2
7/8←←←←←←←←←←←→
𝐴𝑐
𝐴
1/3←←←←←←←←←←←→ 1/5←←←←←←←←←←←→
𝐿3
4/5←←←←←←←←←←←→
𝐴𝑐
  1. Por el teorema de la probabilidad total, la probabilidad de que no haya acertado con la llave seleccionada es: 𝑃(𝐴𝑐)=𝑃(𝐴𝑐∩𝐿1)+𝑃(𝐴𝑐∩𝐿2)+𝑃(𝐴𝑐∩𝐿3)==𝑃(𝐿1)⋅𝑃(𝐴𝑐|𝐿1)+𝑃(𝐿2)⋅𝑃(𝐴𝑐|𝐿2)+𝑃(𝐿3)⋅𝑃(𝐴𝑐|𝐿3)=13⋅67+13⋅78+13⋅45≈0,8440.
  2. La probabilidad de que el llavero sea el tercero y la llave abra el trastero es: 𝑃(𝐿3∩𝐴)=𝑃(𝐿3)⋅𝑃(𝐴|𝐿3)=13⋅15=115≈0,0667.
  3. La probabilidad de que la llave pertenezca al primer o al tercer llavero sabiendo que abre el trastero es: 𝑃((𝐿1∪𝐿3)|𝐴)=𝑃((𝐿1∪𝐿3)∩𝐴)𝑃(𝐴)=𝑃(𝐿1∩𝐴)+𝑃(𝐿3∩𝐴)1−𝑃(𝐴𝑐)=𝑃(𝐿1)⋅𝑃(𝐴|𝐿1)+𝑃(𝐿3)⋅𝑃(𝐴|𝐿3)1−𝑃(𝐴𝑐)==13⋅17+13⋅151−0,8440≈0,7328.
  4. La probabilidad de que la llave no pertenezca al primer llavero sabiendo que no abre el trastero es: 𝑃(𝐿𝑐1|𝐴𝑐)=𝑃(𝐿𝑐1∩𝐴𝑐)𝑃(𝐴𝑐)=𝑃(𝐿2∩𝐴𝑐)+𝑃(𝐿3∩𝐴𝑐)𝑃(𝐴𝑐)=𝑃(𝐿2)⋅𝑃(𝐴𝑐|𝐿2)+𝑃(𝐿3)⋅𝑃(𝐴𝑐|𝐿3)𝑃(𝐴𝑐)==13⋅78+13⋅450,8440≈0,6615.

Ejercicio 5

Una empresa de marketing ha lanzado una campaña publicitaria para promocionar un nuevo servicio de energía solar para hogares. Según estudios previos, se estima que el 20% de las personas que ven el anuncio terminan contratando el servicio. Para analizar más en profundidad la efectividad de la campaña, se seleccionan aleatoriamente a 20 personas que han visto el anuncio.

  1. Calcule la probabilidad de que exactamente 10 personas contraten el servicio.
  2. Determine la probabilidad de que al menos 2 personas contraten el servicio.
  3. Determine el valor esperado del número de personas que contratarán el servicio de entre las seleccionadas.
  4. ¿Cuántas personas, de entre las que han visto el anuncio, se deberían seleccionar para que el número esperado de personas que contraten el servicio sea mayor o igual a 13?

Resolución

Llamamos 𝑋 al número de personas que contratan el servicio, con 𝑋 ∼Bi⁡(𝑛 =20, 𝑝 =0,2).

  1. La probabilidad de que 10 personas contraten el servicio es: 𝑃(𝑋=10)=(2010)0,210⋅0,810≈0,0020.
  2. En primer lugar, hallamos la probabilidad de que contraten el servicio menos de 2 personas. 𝑃(𝑋=0)=(200)0,20⋅0,820≈0,0115,𝑃(𝑋=1)=(201)0,21⋅0,819≈0,0576. Así que: 𝑃(𝑋≤1)=𝑃(𝑋=0)+𝑃(𝑋=1)=0,0115+0,0576=0,0691. Por tanto, la probabilidad de que contraten el servicio al menos 2 personas es: 𝑃(𝑋≥2)=1−𝑃(𝑋≤1)=1−0,0691=0,9309.
  3. El valor esperado viene dado por: 𝐸(𝑋)=𝑛𝑝=20⋅0,2=4.
  4. Para que el valor esperado sea 13, ha de verificarse: 𝐸(𝑋)=13⇔𝑛𝑝=13⇔0,2𝑛=13⇔𝑛=65. Por tanto, se deberían seleccionar al menos 65 personas.

Ejercicio 6

El tiempo de estudio semanal de los estudiantes andaluces, medido en horas, se distribuye según una ley Normal de media desconocida y desviación típica 5 horas. A partir de una muestra de 81 estudiantes se ha obtenido que el intervalo de confianza para la media poblacional es (10,794; 13,206), con un nivel de confianza del 97%.

  1. Obtenga el tiempo medio de estudio de esa muestra de estudiantes.
  2. Si se amplía el tamaño de la muestra, razone si manteniendo el nivel de confianza, la amplitud del intervalo de confianza aumenta o disminuye.
  3. Si se desea reducir la amplitud del intervalo de confianza, razone si manteniendo el tamaño muestral, ha de reducirse o aumentarse el nivel de confianza.
  4. Si la media de la población es de 10,2 horas y sabiendo que la media muestral es de 12 horas, calcule el tamaño máximo de la muestra para obtener un intervalo de confianza que contenga la media poblacional, manteniendo el 97% de confianza.

Resolución
  1. La media muestral viene dada por el punto medio del intervalo. ¯𝑥=10,704+13,2062=12.
  2. La amplitud del intervalo disminuye al aumentar el tamaño de la muestra, porque el error máximo cometido se reduce.
  3. El nivel de confianza debe reducirse para disminuir la amplitud del intervalo, porque el error máximo cometido se reduce.
  4. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Como el nivel de confianza es del 97%, entonces: 𝑃(𝑍≤𝑧𝛼/2)=1+0,972=0,985⇔𝑧𝛼/2=2,17. Así que el intervalo de confianza para estimar la media de la población con un nivel de confianza del 97% es: 𝐼=(12−2,17⋅5√𝑛,12+2,17⋅5√𝑛)=(12−10,85√𝑛,12+10,85√𝑛). Para que el intervalo contenga a la media poblacional 𝜇 =10,2, ha de verificarse: 12−10,85√𝑛=10,2⇔10,85√𝑛=1,8⇔√𝑛=10,851,8⇔𝑛=10,8521,82≈36,3341. Por tanto, el tamaño máximo de la muestra debe ser de 36 estudiantes.

Ejercicio 7

Los desajustes sobre el horario previsto de llegada de los trenes de alta velocidad, medidos en minutos, siguen una ley Normal con media 0 y desviación típica 2,2.

  1. Calcule el porcentaje de trenes que tienen un desajuste máximo de un minuto.
  2. Elegidos al azar 15 trenes de alta velocidad, los desajustes han sido: 01,3−2,1−1,520,852,1−31,83,14−0,71,6−5,4.
    1. Calcule un intervalo de confianza, con un nivel de confianza del 96%, para la media poblacional. ¿Cuál es el error máximo que se comete en la estimación de esta media? Con ese nivel de confianza y a partir de los datos obtenidos, ¿puede afirmarse que un tren tenga un retraso de 2 minutos?
    2. Con un nivel de confianza del 98%, ¿cuántos trenes de alta velocidad deberían elegirse, como mínimo, para que la diferencia entre la media poblacional y su estimación muestral sea como máximo de 1,1 minutos?

Resolución
  1. El desajuste sobre el horario previsto 𝑋 sigue una distribución 𝑁(0; 2,2). La probabilidad de que un tren tenga un desajuste máximo de 1 minuto es: 𝑃(−1≤𝑋≤1)=𝑃(−12,2≤𝑍≤12,2)=𝑃(−0,45≤𝑍≤0,45)=𝑃(𝑍≤0,45)−𝑃(𝑍≤−0,45)==𝑃(𝑍≤0,45)−(1−𝑃(𝑍≤0,45))=2𝑃(𝑍≤0,45)−1=2⋅0,6736−1=0,3472. Por tanto, el porcentaje de trenes que tienen un desajuste máximo de 1 minuto es el 34,72%.
    1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Calculamos la media muestral. ――𝑥=0+1,3−2,1−1,5+2+0,8+5+2,1−3+1,8+3,1+4−0,7+1,6−5,415=0,6. Como el nivel de confianza es del 96%, entonces: 𝛼=1−0,96=0,04⇒1−𝛼2=1−0,042=0,98⇒𝑧𝛼/2=2,055. Por tanto, el intervalo de confianza para estimar el desajuste medio en minutos de los trenes con un nivel de confianza del 96% es: 𝐼=(0,6−2,055⋅2,2√15,0,6+2,055⋅2,2√15)≈(−0,5673;1,7673). El error máximo cometido con esta estimación viene dado por: 𝐸=1,7673−(−0,5673)2=1,1673. Como 2 no pertenece al intervalo de confianza, no puede afirmarse que un tren tenga un retraso de 2 minutos.
    2. Si el nivel de confianza es del 98%, entonces: 𝛼=1−0,98=0,02⇒1−𝛼2=1−0,022=0,99⇒𝑧𝛼/2=2,325. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=2,325⋅2,2√𝑛=5,115√𝑛. Para que el error máximo no sea superior a 1,1, ha de verificarse que: 𝐸=1,1⇔5,115√𝑛=1,1⇔√𝑛=4,65⇔𝑛=21,6225. Por tanto, el numero mínimo de trenes de la muestra debe ser 22.