Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 4 de 2022

Ejercicio 1

Una fábrica de juguetes educativos produce juegos de ajedrez y dominó. Para fabricar un ajedrez se necesitan 2kg de madera y 4 horas de trabajo, mientras que para fabricar un dominó se necesita 1kg de madera y 1 hora de trabajo. Para que la producción sea rentable hay que hacer al día al menos 3 juegos y emplear como máximo 7kg de madera y 9 horas de trabajo. Cada ajedrez se vende por 40€ y cada dominó por 15€. ¿Cuántos juegos de ajedrez y dominó deben fabricarse diariamente para que la ganancia obtenida sea máxima? ¿Cuál será esa ganancia?

Resolución

Llamamos 𝑥 al número de juegos de ajedrez e 𝑦 al de dominó. Podemos organizar la información en una tabla.

Madera (kg) Trabajo (h) Precio (€)
Ajedrez 2 4 40
Dominó 1 1 15
Máximo 7 9

Las restricciones del problema son: ⎧{ { { {⎨{ { { {⎩2𝑥+𝑦≤7,4𝑥+𝑦≤9,𝑥+𝑦≤3,𝑥≥0,𝑦≥0. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=40𝑥+15𝑦.

Representamos la región factible. 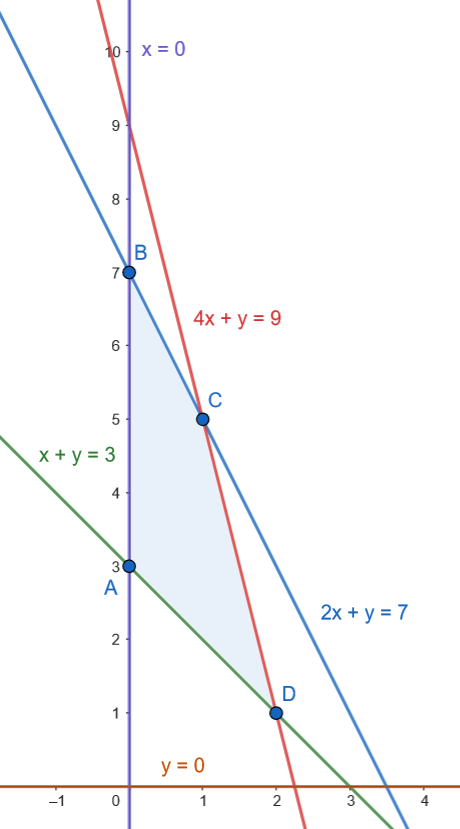Figura Los vértices son: 𝐴(0,3),𝐵(0,7),𝐶(1,5)y𝐷(2,1).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(0,3)=45,𝐹(𝐵)=𝐹(0,7)=105,𝐹(𝐶)=𝐹(1,5)=115,𝐹(𝐷)=𝐹(2,1)=95. Por tanto, la ganancia máxima se alcanza fabricando 1 juego de ajedrez y 5 juegos de dominó diarios, con unos beneficios de 115€.

Ejercicio 2

Se consideran las matrices 𝐴=⎛⎜ ⎜ ⎜⎝7−6−2314−50−4⎞⎟ ⎟ ⎟⎠,𝐵=⎛⎜ ⎜ ⎜⎝223534−401⎞⎟ ⎟ ⎟⎠,𝐶=(12−1−2−30)y𝐷=(𝑎20−11−1𝑎).

  1. Resuelva la siguiente ecuación matricial: 𝐴𝑡 −𝑋𝐴 =3𝐼3.
  2. ¿Existe algún valor del parámetro 𝑎 para el que se verifique 𝐶𝑡𝐷 =𝐵? En caso afirmativo, calcule dicho valor.

Resolución
  1. En primer lugar, calculamos el determinante de la matriz 𝐴. |𝐴|=∣7−6−2314−50−4∣=10. Así que 𝐴 es invertible con det(𝐴) =10. Despejamos la ecuación matricial. 𝐴𝑡−𝑋𝐴=3𝐼3⇔𝑋𝐴=𝐴𝑡−3𝐼3⇔𝑋=(𝐴𝑡−3𝐼3)𝐴−1. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝−4−85−24−3830−22−3425⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=110⎛⎜ ⎜ ⎜⎝−4−24−22−8−38−2453025⎞⎟ ⎟ ⎟⎠. Por último, calculamos la matriz 𝑋 operando. 𝑋=(𝐴𝑡−3𝐼3)𝐴−1=110⎡⎢ ⎢⎣⎛⎜ ⎜ ⎜⎝73−5−610−24−4⎞⎟ ⎟ ⎟⎠−⎛⎜ ⎜ ⎜⎝300030003⎞⎟ ⎟ ⎟⎠⎤⎥ ⎥⎦⎛⎜ ⎜ ⎜⎝−4−24−22−8−38−2453025⎞⎟ ⎟ ⎟⎠==110⎛⎜ ⎜ ⎜⎝43−5−6−20−24−7⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝−4−24−22−8−38−2453025⎞⎟ ⎟ ⎟⎠=110⎛⎜ ⎜ ⎜⎝−65−360−31540220200−59−314−297⎞⎟ ⎟ ⎟⎠.
  2. Veamos cuándo 𝐶𝑡𝐷 =𝐵. 𝐶𝑡𝐷=𝐵⇔⎛⎜ ⎜ ⎜⎝1−22−3−10⎞⎟ ⎟ ⎟⎠(𝑎20−11−1𝑎)=⎛⎜ ⎜ ⎜⎝223534−401⎞⎟ ⎟ ⎟⎠⇔⎛⎜ ⎜ ⎜ ⎜⎝𝑎2−22−1−2𝑎2𝑎2−33−2−3𝑎−𝑎201⎞⎟ ⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝223534−401⎞⎟ ⎟ ⎟⎠. Igualando los elementos de las matrices, obtenemos el sistema ⎧{ { { {⎨{ { { {⎩𝑎2−2=2⇒𝑎=±2,−1−2𝑎=3⇒𝑎=−2,2𝑎2−3=5⇒𝑎=±2,−2−3𝑎=4⇒𝑎=−2,−𝑎2=−4⇒𝑎=±2. Por tanto, 𝑎 = −2.

Ejercicio 3

Una empresa de fumigación sabe que los beneficios, en miles de euros, que obtiene en función de las hectáreas que le encargan fumigar mensualmente viene dada por la expresión 𝐵(𝑥)=−𝑥2+16𝑥−48. Además, por problemas de personal, la empresa no puede fumigar más de 10 hectáreas al mes.

  1. ¿Cuántas hectáreas tiene que fumigar al mes para que la empresa tenga beneficios?
  2. ¿Cuántas hectáreas tiene que fumigar para obtener el máximo beneficio mensual? ¿A cuánto asciende dicho beneficio?
  3. Si un mes ha obtenido un beneficio de 7.000€, ¿cuántas hectáreas ha fumigado?

Resolución

Como la empresa no puede fumigar más de 10 hectáreas al mes, Dom⁡(𝐵) =[0,10].

  1. Hallamos los puntos de corte de la función 𝐵 con el eje 𝑋, es decir, aquellos en los que el beneficio es cero. 𝐵(𝑥)=0⇔−𝑥2+16𝑥−48=0⇔{𝑥=4,𝑥=12. Así que el único punto de corte con el eje en el dominio [0,10] está en 𝑥 =4. Observamos además que 𝐵(𝑥) >0 si 4 <𝑥 ≤10. Por tanto, la empresa obtendrá beneficios si fumiga entre 4 y 10 hectáreas al mes.
  2. La función es cuadrática y su gráfica es cóncava, así que el máximo se alcanza en el vértice de la parábola. Como el vértice es el punto (8,16), la empresa tendrá que fumigar 8 hectáreas al mes para obtener el beneficio máximo, que asciende a 16.000€.
  3. Se obtiene un beneficio de 7.000€ si 𝐵(𝑥) =7. 𝐵(𝑥)=7⇔−𝑥2+16𝑥−48=7⇔−𝑥2+16𝑥−55=0⇔{𝑥=5,𝑥=11. Como 𝑥 =11 no pertenece al dominio, la función solo alcanza un valor de 7 en 𝑥 =5. Por tanto, la empresa ha fumigado 5 hectáreas.

Ejercicio 4

Se considera la función 𝑓(𝑥)=⎧{ {⎨{ {⎩𝑎𝑥2+𝑏𝑥+1,si 𝑥≤1,2𝑥,si 𝑥>1, con 𝑎 y 𝑏 números reales.

  1. ¿Para qué valores de 𝑎 y 𝑏 la función es continua y derivable en 𝑥 =1?
  2. Para 𝑎 = −3 y 𝑏 =4, calcule los extremos relativos de 𝑓.
  3. Para 𝑎 = −2 y 𝑏 =3, calcule el valor de la integral ∫3−1𝑓(𝑥)𝑑𝑥.

Resolución
    • Si 𝑥 ≠1, 𝑓 es continua y derivable con 𝑓′(𝑥)={2𝑎𝑥+𝑏,si 𝑥<1,−2𝑥2,si 𝑥>1.
    • Estudiamos la continuidad para 𝑥 =1. lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡(𝑎𝑥2+𝑏𝑥+1)=𝑎+𝑏+1,lím𝑥→1+⁡𝑓(𝑥)=lím𝑥→1+⁡2𝑥=2,𝑓(1)=𝑎+𝑏+1. Para que 𝑓 sea continua en 𝑥 =1, ha de verificarse 𝑎+𝑏+1=2⇔𝑎+𝑏=1. Pasamos a estudiar la derivabilidad. 𝑓′−(1)=lím𝑥→1−⁡𝑓′(𝑥)=lím𝑥→1−⁡(2𝑎𝑥+𝑏)=2𝑎+𝑏,𝑓′+(1)=lím𝑥→1+⁡𝑓′(𝑥)=lím𝑥→1+−2𝑥2=−2. Para que 𝑓 sea derivable en 𝑥 =1, ha de verificarse 2𝑎+𝑏=−2.
    Con estas dos condiciones, planteamos el sistema de ecuaciones {𝑎+𝑏=1,2𝑎+𝑏=−2. Resolvemos el sistema por reducción. Si restamos las ecuaciones, obtenemos que −𝑎=3⇔𝑎=−3. Despejando y sustituyendo en la primera ecuación, 𝑎+𝑏=1⇔𝑏=1−𝑎𝑎=−3←←←←←←←→𝑏=4. Por tanto, 𝑎 = −3 y 𝑏 =4.
  2. Si 𝑎 = −3 y 𝑏 =4, por el apartado anterior 𝑓 es continua y derivable en ℝ con 𝑓(𝑥)=⎧{ {⎨{ {⎩−3𝑥2+4𝑥+1,si 𝑥<1,2𝑥,si 𝑥≥1y𝑓′(𝑥)={−6𝑥+4,si 𝑥<1,−2𝑥2,si 𝑥≥1. Para hallar los puntos críticos, igualamos las dos ramas de la derivada a cero.
    • Si 𝑥 <1, 𝑓′(𝑥)=0⇔−6𝑥+4=0⇔𝑥=23.
    • Si 𝑥 ≥1, 𝑓′(𝑥)=−2𝑥2≠0.
    Así que el único punto crítico es 𝑥 =23. Estudiamos el signo de la derivada.
    (−∞,23) (23,+∞)
    signo de 𝑓′ + −
    monotonía de 𝑓 → →
    Por tanto, el punto (23,73) es un máximo relativo.
  3. Si 𝑎 = −2 y 𝑏 =3, 𝑓(𝑥)=⎧{ {⎨{ {⎩−2𝑥2+3𝑥+1,si 𝑥<1,2𝑥,si 𝑥≥1. Calculamos la integral. ∫3−1𝑓(𝑥)𝑑𝑥=∫1−1(−2𝑥2+3𝑥+1)𝑑𝑥+∫312𝑥𝑑𝑥=[−23𝑥3+32𝑥2+𝑥]1−1+[2ln⁡(𝑥)]31==−23+32+1−(23+32−1)+2ln⁡(3)=23+2ln⁡(3).

Ejercicio 5

Juan realiza el siguiente juego: lanza dos dados simultáneamente y si la suma es 2 o mayor que 7, gana y termina el juego. En caso contrario, tiene una segunda y última oportunidad lanzando de nuevo los dos dados y ganaría si la suma es mayor que 9.

  1. ¿Cuál es la probabilidad de que Juan gane lanzando una sola vez los dados?
  2. ¿Cuál es la probabilidad de que Juan gane en la segunda oportunidad?
  3. ¿Cuál es la probabilidad de que Juan gane?

Resolución

Llamamos 𝐺1 a ganar en la primera oportunidad y 𝐺2 a ganar en la segunda. Podemos hacer un diagrama de árbol.

𝐺1
←←←←←←←←→
𝐺2
←←←←←←←←→ ←←←←←←←←→
𝐺𝑐1
←←←←←←←←→
𝐺𝑐2
Para hallar las probabilidades, podemos hacer una tabla con todas las posibilidades al lanzar dos dados.
1 2 3 4 5 6
1 2 3 4 5 6 7
2 3 4 5 6 7 8
3 4 5 6 7 8 9
4 5 6 7 8 9 10
5 6 7 8 9 10 11
6 7 8 9 10 11 12

  1. La probabilidad de que Juan gane lanzando una sola vez los dados es 𝑃(𝐺1)=1636=49.
  2. La probabilidad de que Juan gane en la segunda oportunidad sabiendo que no ganó en la primera es 𝑃(𝐺2|𝐺𝑐1)=636=16. Por tanto, la probabilidad de que Juan gane en la segunda oportunidad es 𝑃(𝐺2)=𝑃(𝐺𝑐1)⋅𝑃(𝐺2|𝐺𝑐1)=59⋅16=554.
  3. La probabilidad de que Juan gane es 𝑃(𝐺1)+𝑃(𝐺2)=49+554=2954.

Ejercicio 6

Una encuesta realizada a los clientes de un banco muestra que el 60% de sus clientes tiene un ordenador, el 50% tiene una tablet y el 20% posee un ordenador y una tablet. Se elige al azar un cliente de ese banco.

  1. Calcule la probabilidad de que:
    1. Tenga un ordenador o una tablet.
    2. No tenga tablet si no tiene ordenador.
    3. Tenga ordenador y no tenga tablet.
  2. ¿Son los sucesos "Tener un ordenador" y "Tener una tablet" incompatibles? ¿Son sucesos independientes?

Resolución

Llamamos 𝑂 a tener un ordenador y 𝑇 a tener una tablet. Sabemos que 𝑃(𝑂)=0,6,𝑃(𝑇)=0,5y𝑃(𝑂∩𝑇)=0,2.

    1. La probabilidad de que tenga un ordenador o una tablet es 𝑃(𝑂∪𝑇)=𝑃(𝑂)+𝑃(𝑇)−𝑃(𝑂∩𝑇)=0,6+0,5−0,2=0,9.
    2. La probabilidad de que no tenga tablet sabiendo que no tiene ordenador es 𝑃(𝑇𝑐|𝑂𝑐)=𝑃(𝑇𝑐∩𝑂𝑐)𝑃(𝑂𝑐)=𝑃((𝑇∪𝑂)𝑐)1−𝑃(𝑂)=1−𝑃(𝑇∪𝑂)1−𝑃(𝑂)=1−0,91−0,6=0,25.
    3. La probabilidad de que tenga ordenador y no tenga tablet es 𝑃(𝑂∩𝑇𝑐)=𝑃(𝑂)−𝑃(𝑂∩𝑇)=0,6−0,2=0,4.
  2. Como 𝑃(𝑂 ∩𝑇) >0, los sucesos no son incompatibles. Por otro lado, como 𝑃(𝑇𝑐|𝑂𝑐) ≠𝑃(𝑇𝑐), los sucesos no son independientes.

Ejercicio 7

Se desea estimar la proporción de personas mayores de 45 años de una determinada ciudad que tienen presbicia (vista cansada). Para ello, se toma una muestra aleatoria de 540 personas mayores de 45 años, obteniéndose que 378 tienen presbicia.

  1. Obtenga un intervalo, con un nivel de confianza del 97%, para estimar la proporción poblacional de personas mayores de 45 años con presbicia en dicha ciudad.
  2. Suponiendo que se mantiene la misma proporción muestral y el mismo nivel de confianza del apartado anterior, ¿cuántas personas se deberán seleccionar como mínimo para que la proporción muestral difiera de la proporción poblacional a lo sumo en un 3%?

Resolución
  1. Como 378 personas de 𝑛 =540 tienen vista cansada, la proporción muestral es: 𝑝=378540=0,7. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar la proporción de personas mayores de 45 años con vista cansada en la ciudad con un nivel de confianza del 97% es: 𝐼=(0,7−2,17⋅√0,7⋅(1−0,7)540,0,7+2,17⋅√0,7⋅(1−0,7)540)≈(0,6572;0,7428).
  2. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=2,17⋅√0,7⋅(1−0,7)𝑛=2,17⋅√0,21𝑛. Si se quiere el error no sea mayor que 0,03, entonces: 2,17⋅√0,21𝑛=0,03⇔√0,21𝑛=0,032,17⇔0,21𝑛=0,0322,172⇔𝑛=0,21⋅2,1720,032≈1.098,7433. Por tanto, el número mínimo de personas de la muestra debe ser 1.099.

Ejercicio 8

El peso en gramos de las tortugas terrestres de una reserva natural sigue una ley Normal de varianza 121g2. Para estimar el peso medio de las tortugas de la reserva, se toma una muestra de 10 tortugas, obteniéndose los siguientes datos: 98010029509851100108589510009121006.

  1. Halle un intervalo de confianza para el peso medio de las tortugas con un nivel de confianza del 97%.
  2. ¿Cuál debe ser el tamaño mínimo de la muestra para asegurar con un nivel de confianza del 94% que el error máximo cometido sea de 5g?

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Calculamos la media muestral. ――𝑥=980+1002+950+985+1100+1085+895+1000+912+100610=991,5. Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar el peso medio de las tortugas con un nivel de confianza del 97% es: 𝐼=(991,5−2,17⋅√121√10,991,5+2,17⋅√121√10)≈(983,9516;999,0484).
  2. Si el nivel de confianza es del 94%, entonces: 𝛼=1−0,94=0,06⇒1−𝛼2=1−0,062=0,97⇒𝑧𝛼/2=1,885. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=1,885⋅√121√𝑛=20,735√𝑛. Si se quiere que el error máximo cometido sea de 5, entonces: 20,735√𝑛=5⇔√𝑛=20,7355⇔𝑛=20,735225≈17,1976. Por tanto, el tamaño mínimo de la muestra debe ser de 18 tortugas.