Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 2 de 2022

Ejercicio 1

Se considera el recinto definido por las siguientes inecuaciones: 𝑥+2𝑦≥7,2𝑥−𝑦≤4,4𝑥−𝑦≥1,3𝑥+2𝑦≤20.

  1. Represente dicho recinto y calcule sus vértices.
  2. Obtenga el valor máximo de la función 𝐹(𝑥,𝑦) =𝑥 +3𝑦 en el recinto anterior, así como el punto donde se alcanza.

Resolución
  1. Representamos el recinto. 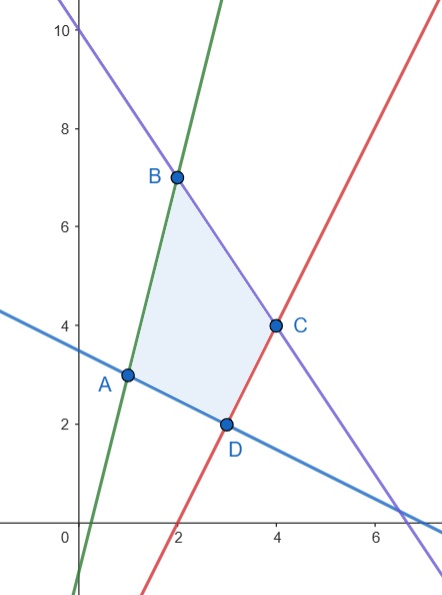Figura Los vértices son 𝐴(1,3),𝐵(2,7),𝐶(4,4)y𝐷(3,2).
  2. Para hallar el valor máximo de la función 𝐹, la evaluamos en los vértices. 𝐹(𝐴)=𝐹(1,3)=10,𝐹(𝐵)=𝐹(2,7)=23,𝐹(𝐶)=𝐹(4,4)=16,𝐹(𝐷)=𝐹(3,2)=9. Por tanto, el máximo se alcanza en el punto 𝐵(2,7) y el valor de la función es 23.

Ejercicio 2

Se consideran las matrices 𝐴=⎛⎜ ⎜ ⎜⎝𝑎208𝑎000𝑎⎞⎟ ⎟ ⎟⎠y𝐵=⎛⎜ ⎜ ⎜⎝1−210⎞⎟ ⎟ ⎟⎠, donde 𝑎 es un número real.

  1. Determine los valores de 𝑎 para que la matriz 𝐴 sea no invertible.
  2. Para 𝑎 =5, calcule la inversa de la matriz 𝐴.
  3. Para 𝑎 =5, resuelva la ecuación matricial 𝐴𝑋 =𝐵.

Resolución
  1. Calculamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣𝑎208𝑎000𝑎∣=𝑎3−16𝑎. La inversa de 𝐴 existe si y solo si su determinante es no nulo. |𝐴|=0⇔𝑎3−16𝑎=0⇔𝑎(𝑎2−16)=0⇔{𝑎=0,𝑎2−16=0⇔𝑎2=16⇔𝑎=±4. Por tanto, la matriz 𝐴 es no invertible si 𝑎 = −4, 𝑎 =0 o 𝑎 =4.
  2. Si 𝑎 =5, por el apartado anterior 𝐴 es invertible con det(𝐴) =45. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝25−400−10250009⎞⎟ ⎟ ⎟⎠. Calculamos su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=145⎛⎜ ⎜ ⎜⎝25−100−40250009⎞⎟ ⎟ ⎟⎠.
  3. Despejamos 𝑋 en la ecuación matricial y resolvemos. 𝐴𝑋=𝐵⇔𝑋=𝐴−1𝐵=145⎛⎜ ⎜ ⎜⎝25−100−40250009⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝1−210⎞⎟ ⎟ ⎟⎠=145⎛⎜ ⎜ ⎜⎝45−9090⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝1−22⎞⎟ ⎟ ⎟⎠.

Ejercicio 3

Los ingresos (𝐼) y los costes (𝐶) de una discoteca, en miles de euros, en función del número de horas diarias que permanece abierta, vienen dados por las funciones: 𝐼(𝑥)=𝑥3−𝑥y𝐶(𝑥)=𝑥3−𝑥2+6, respectivamente. Sabiendo que la licencia del ayuntamiento no permite que este tipo de local permanezca abierto más de 8 horas diarias, halle:

  1. La función beneficio en función del número de horas diarias que la discoteca permanece abierta.
  2. El número de horas que debe permanecer abierta para obtener beneficios.
  3. En qué momento se tienen las mayores pérdidas y a cuánto ascienden.
  4. El tiempo que debe permanecer abierta para obtener el máximo beneficio y a cuánto asciende.

Resolución
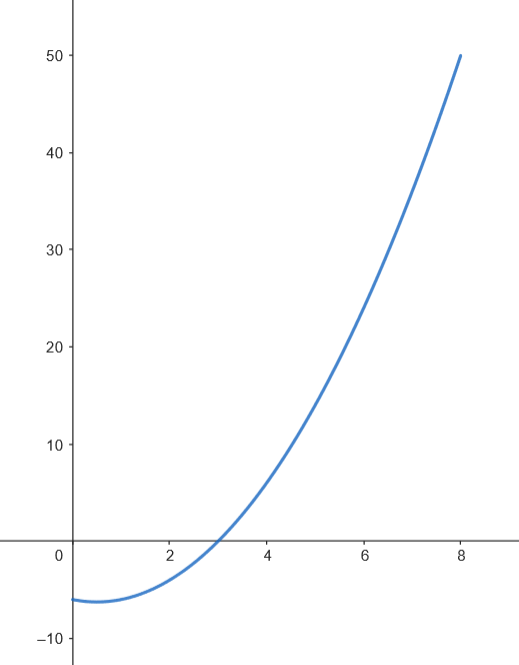
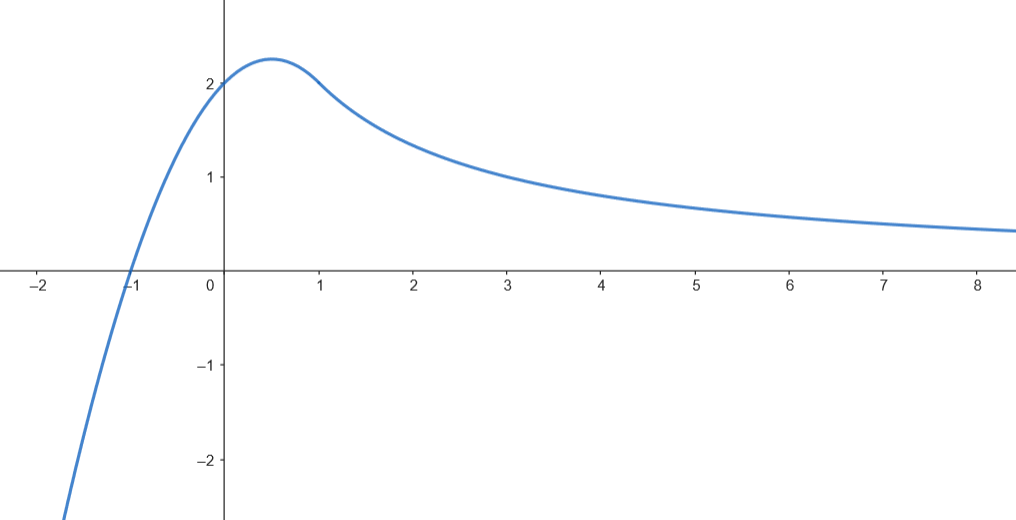
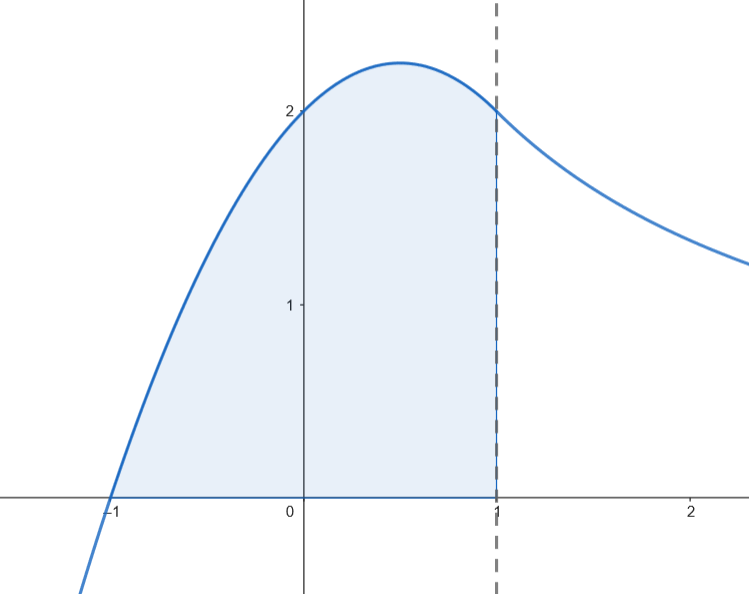  1. Los beneficios viene dados por la diferencia entre los ingresos y los costes. La función que representa los beneficios en miles de euros en función del número de horas diarias es 𝐵(𝑥)=𝐼(𝑥)−𝐶(𝑥)=𝑥3−𝑥−(𝑥3−𝑥2+6)=𝑥2−𝑥−6,0≤𝑥≤8. Podemos representar la función Figura
  2. Hallamos los puntos de corte de 𝐵 con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝐵(𝑥)=0⇔𝑥2−𝑥−6=0⇔{𝑥=−2,𝑥=3. Así que el único punto de corte con el eje en el dominio [0,8] está en 𝑥 =3. Observamos además que 𝐵(𝑥) >0 para 𝑥 >3. Por tanto, la discoteca obtiene beneficios a partir de la tercera hora.
  3. La función 𝐵 es una parábola cóncava con vértice (0,5; −6,25), por lo que este es su mínimo absoluto. Por tanto, la discoteca tiene las mayores pérdidas a la media hora y estas ascienden a 6.250€.
  4. El máximo absoluto de la función es el punto (8,50). Por tanto, se obtiene el máximo beneficio a las ocho horas y este asciende a 50.000€.

Ejercicio 4

Se considera la función 𝑓(𝑥)=⎧{ {⎨{ {⎩𝑎𝑥2+𝑏𝑥+2,si 𝑥≤1,4𝑥+1,si 𝑥>1, con 𝑎 y 𝑏 números reales.

  1. Calcule 𝑎 y 𝑏 para que la función 𝑓 sea continua y derivable.
  2. Para 𝑎 = −1 y 𝑏 =1, realice un esbozo de la gráfica de la función 𝑓.
  3. Para 𝑎 = −1 y 𝑏 =1, halle el área del recinto acotado, limitado por la gráfica de 𝑓, la recta 𝑥 =1 y el eje 𝑂𝑋.

Resolución
    • Si 𝑥 ≠1, 𝑓 es continua y derivable con 𝑓′(𝑥)=⎧{ {⎨{ {⎩2𝑎𝑥+𝑏,si 𝑥<1,−4(𝑥+1)2,si 𝑥>1.
    • Estudiamos la continuidad para el punto de ruptura 𝑥 =1. lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡(𝑎𝑥2+𝑏𝑥+2)=𝑎+𝑏+2,lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡4𝑥+1=2,𝑓(1)=𝑎+𝑏+2. Para que 𝑓 sea continua, ha de verificarse 𝑎+𝑏+2=2⇔𝑎+𝑏=0. Pasamos a estudiar la derivabilidad. 𝑓′−(1)=lím𝑥→1−⁡𝑓′(𝑥)=lím𝑥→1−⁡(2𝑎𝑥+𝑏)=2𝑎+𝑏,𝑓′+(1)=lím𝑥→1+⁡𝑓′(𝑥)=lím𝑥→1+−4(𝑥+1)2=−1. Para que 𝑓 sea derivable, ha de verificarse 2𝑎+𝑏=−1.
    Con estas dos condiciones, planteamos el sistema de ecuaciones {𝑎+𝑏=0,2𝑎+𝑏=−1. Resolvemos el sistema por reducción. Si restamos las ecuaciones, obtenemos que −𝑎=1⇔𝑎=−1. Despejando y sustituyendo en la primera ecuación, 𝑎+𝑏=0⇔𝑏=−𝑎𝑎=−1←←←←←←←→𝑏=1. Por tanto, 𝑎 = −1 y 𝑏 =1.
  2. Si 𝑎 = −1 y 𝑏 =1, sabemos por el apartado anterior que 𝑓 es continua y derivable. Representamos gráficamente la función. Observamos que la parábola tiene vértice (0,5; 2,25) y corta a los ejes en los puntos ( −1,0) y (0,2). Figura
  3. Podemos representar el recinto acotado limitado por la gráfica de 𝑓, el eje 𝑋 y la recta 𝑥 =1. Figura Calculamos el área. ∫1−1𝑓(𝑥)𝑑𝑥=∫1−1(−𝑥2+𝑥+2)𝑑𝑥=[−13𝑥3+12𝑥2+2𝑥]1−1=−13+12+2−(13+12−2)=103𝑢2.

Ejercicio 5

Se ha llevado a cabo una encuesta en un centro educativo para saber qué actividades extraescolares se realizan por la tarde. El 80% de los encuestados practican deporte o estudian idiomas, el 35% realizan ambas actividades y el 60% no estudian idiomas.

  1. Elegido un estudiante de ese centro al azar, calcule la probabilidad de que:
    1. Practique deporte y no estudie idiomas.
    2. Estudie idiomas y no practique deporte.
    3. Haga solamente una de las dos actividades.
    4. No haga ninguna de las dos actividades.
  2. ¿Son independientes los sucesos "Practicar deporte" y "Estudiar idiomas"?

Resolución

Llamamos 𝐷 a practicar deporte e 𝐼 a estudiar idiomas. Sabemos que: 𝑃(𝐷∪𝐼)=0,8,𝑃(𝐷∩𝐼)=0,35y𝑃(𝐼𝑐)=0,6⇒𝑃(𝐼)=0,4.

    1. Sabemos que la probabilidad de practicar deporte o estudiar idiomas viene dada por: 𝑃(𝐷∪𝐼)=𝑃(𝐷)+𝑃(𝐼)−𝑃(𝐷∩𝐼). Así que, despejando en la expresión anterior, la probabilidad de practicar deporte es: 𝑃(𝐷)=𝑃(𝐷∪𝐼)+𝑃(𝐷∩𝐼)−𝑃(𝐼)=0,8+0,35−0,4=0,75. Por tanto, la probabilidad de practicar deporte y no estudiar idiomas es: 𝑃(𝐷∩𝐼𝑐)=𝑃(𝐷)−𝑃(𝐷∩𝐼)=0,75−0,35=0,4.
    2. La probabilidad de estudiar idiomas y no practicar deporte es: 𝑃(𝐼∩𝐷𝑐)=𝑃(𝐼)−𝑃(𝐷∩𝐼)=0,4−0,35=0,05.
    3. La probabilidad de hacer solo una de las dos actividades es: 𝑃((𝐷∩𝐼𝑐)∪(𝐷𝑐∩𝐼))=𝑃(𝐷∩𝐼𝑐)+𝑃(𝐷𝑐∩𝐼)=0,4+0,05=0,45.
    4. La probabilidad de no hacer ninguna de las dos actividades es: 𝑃(𝐷𝑐∩𝐼𝑐)=𝑃((𝐷∪𝐼)𝑐)=1−𝑃(𝐷∪𝐼)=1−0,8=0,2.
  2. Observamos que: 𝑃(𝐷)⋅𝑃(𝐼)=0,75⋅0,4=0,3,𝑃(𝐷∩𝐼)=0,35. Como 𝑃(𝐷) ⋅𝑃(𝐼) ≠𝑃(𝐷 ∩𝐼), los sucesos no son independientes.

Ejercicio 6

Del total de personas vacunadas en un país para prevenir una enfermedad, el 48% recibió la vacuna A, el 35% la vacuna B y el resto la vacuna C. La efectividad de la vacuna A se sitúa en el 70%, la de B en el 95% y la de C en el 94%. Elegida al azar una persona vacunada,

  1. ¿Cuál es la probabilidad de que haya sido vacunada con A y no le sea efectiva?
  2. ¿Qué probabilidad hay de que la vacuna le sea efectiva?
  3. Sabiendo que la vacuna no le ha sido efectiva, ¿cuál es la probabilidad de que haya sido vacunada con C?

Resolución

Llamamos 𝐴 a recibir la vacuna A, 𝐵 a recibir la vacuna B, 𝐶 a recibir la vacuna C y 𝐸 a que la vacuna sea efectiva. Podemos hacer un diagrama de árbol.

𝐸
0,7←←←←←←←←←←→
𝐴
0,48←←←←←←←←←←←→ 0,3←←←←←←←←←←→
𝐸𝑐
𝐸
0,95←←←←←←←←←←←→
0,35←←←←←←←←←←←→ 𝐵
0,05←←←←←←←←←←←→
𝐸𝑐
𝐸
0,17←←←←←←←←←←←→ 0,94←←←←←←←←←←←→
𝐶
0,06←←←←←←←←←←←→
𝐸𝑐
  1. La probabilidad de que haya sido vacunada con A y no le sea efectiva es: 𝑃(𝐴∩𝐸𝑐)=𝑃(𝐴)⋅𝑃(𝐸𝑐|𝐴)=0,48⋅0,3=0,144.
  2. Por el teorema de la probabilidad total, la probabilidad de que la vacuna le sea efectiva es: 𝑃(𝐸)=𝑃(𝐴∩𝐸)+𝑃(𝐵∩𝐸)+𝑃(𝐶∩𝐸)=𝑃(𝐴)∩𝑃(𝐸|𝐴)+𝑃(𝐵)∩𝑃(𝐸|𝐵)+𝑃(𝐶)∩𝑃(𝐸|𝐶)==0,48⋅0,7+0,35⋅0,95+0,17⋅0,94=0,8283.
  3. La probabilidad de que haya sido vacunada con C sabiendo que la vacuna no le ha sido efectiva es: 𝑃(𝐶|𝐸𝑐)=𝑃(𝐶∩𝐸𝑐)𝑃(𝐸𝑐)=𝑃(𝐶)⋅𝑃(𝐸𝑐|𝐶)1−𝑃(𝐸)=0,17⋅0,061−0,8283≈0,0594.

Ejercicio 7

Se desea estimar la proporción de jóvenes de una localidad que están suscritos a una determinada plataforma de televisión. Para ello, se toma una muestra aleatoria de 100 jóvenes de los que 36 afirman estar suscritos a dicha plataforma.

  1. Determine un intervalo de confianza, con un nivel del 92%, para la proporción de jóvenes que están suscritos a esta plataforma.
  2. Suponiendo que se mantiene la misma proporción muestral y el mismo nivel de confianza del apartado anterior, determine el tamaño muestral mínimo que se debería tomar si se quisiera que el error máximo fuera 0,025.

Resolución
  1. Como 36 jóvenes de 𝑛 =100 están suscritos a la plataforma, la proporción muestral es: 𝑝=36100=0,36. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 92%, entonces: 𝛼=1−0,92=0,08⇒1−𝛼2=1−0,082=0,96⇒𝑧𝛼/2=1,75. Por tanto, el intervalo de confianza para estimar la proporción poblacional de jóvenes suscritos a la plataforma con un nivel de confianza del 92% es: 𝐼=(0,36−1,75⋅√0,36⋅(1−0,36)100,0,36+1,75⋅√0,36⋅(1−0,36)100)=(0,276;0,444).
  2. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=1,75⋅√0,36⋅(1−0,36)𝑛=0,84√𝑛. Si se quiere que el error máximo sea de 0,025, entonces: 0,84√𝑛=0,025⇔√𝑛=0,840,025⇔𝑛=0,8420,0252=1.128,96. Por tanto, el tamaño mínimo de la muestra debe ser de 1.129 jóvenes.

Ejercicio 8

La vida útil de un determinado modelo de teléfono móvil (en meses) se distribuye según una ley Normal de varianza 9,61 meses2. En una muestra de 10 teléfonos, la vida útil de los mismos ha sido: 30,63031,329,732,33232,831,531,230,5.

  1. Determine un intervalo de confianza para estimar la vida útil de este modelo de teléfono móvil con un nivel de confianza del 97%.
  2. Determine el tamaño mínimo muestral para que, con el mismo nivel de confianza, el error que se comete al estimar la duración media de la vida útil de este modelo de teléfono móvil sea inferior a 0,15 meses.

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Calculamos la media muestral. ――𝑥=30,6+30+31,3+29,7+32,3+32+32,8+31,5+31,2+30,510=31,19. Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar la vida media en meses del teléfono con un nivel de confianza del 97% es: 𝐼=(31,19−2,17⋅√9,61√10,31,19+2,17⋅√9,61√10)≈(29,0627;33,3173).
  2. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=2,17⋅√9,61√𝑛=6,727√𝑛. Si se quiere que el error máximo sea inferior a 0,15, entonces: 6,727√𝑛=0,15⇔√𝑛=6,7270,15⇔𝑛=6,72720,152≈2.011,2235. Por tanto, el tamaño mínimo de la muestra debe ser de 2.012 teléfonos.