Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 3 de 2023

Ejercicio 1

El aforo de un campo de fútbol es de 10.000 personas. Según el reglamento establecido por la federación de fútbol, como máximo deben ponerse a la venta 3.000 entradas para los aficionados del equipo visitante y por cada aficionado visitante debe haber dos aficionados locales como mínimo y cuatro aficionados locales como máximo. Si el precio de la entrada es de 50€ pero el aficionado local tiene un descuento del 20%, ¿cuántos aficionados locales y visitantes deben asistir para obtener el mayor importe con la venta de las entradas?

Resolución

Llamamos 𝑥 al número de aficionados del equipo local que asisten al partido e 𝑦 al de aficionados del equipo visitante.

Las restricciones del problema son: ⎧{ { { {⎨{ { { {⎩𝑥+𝑦≤10.000,𝑦≤3.000,𝑥≥2𝑦,𝑥≤4𝑦,𝑦≥0. Como el precio de la entrada para los aficionados del equipo local es de 50 ⋅0,8 =40€, la función objetivo a maximizar es: 𝐹(𝑥,𝑦)=40𝑥+50𝑦.

Representamos la región factible. 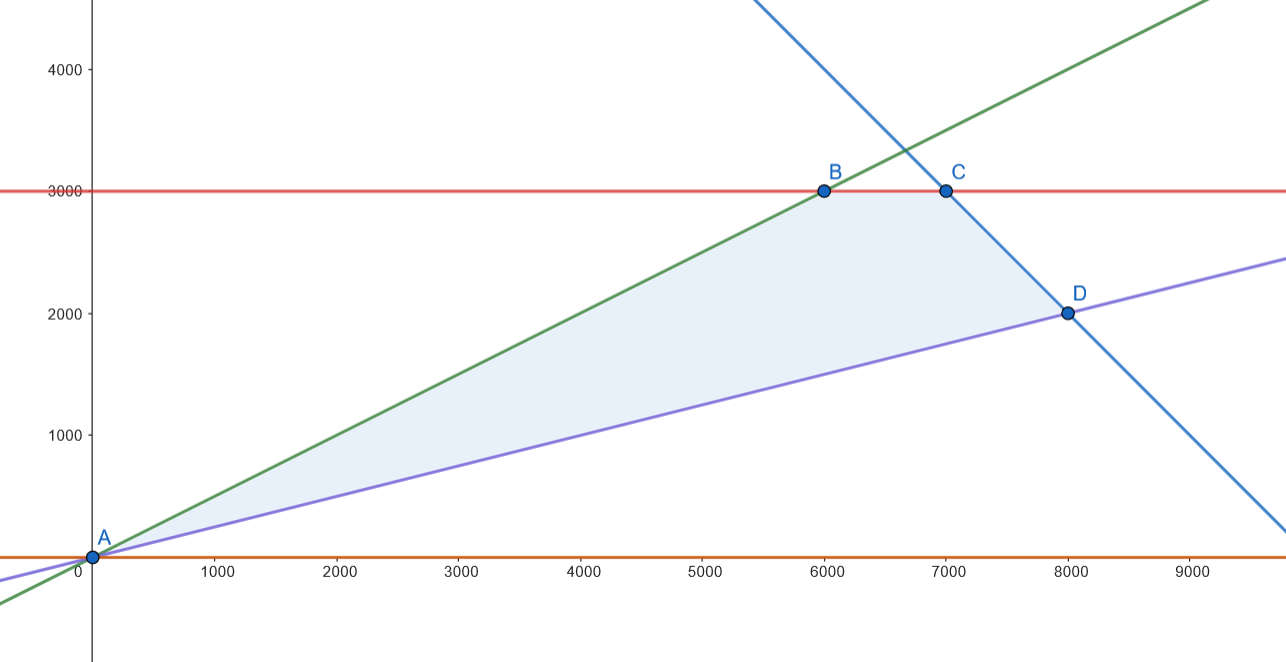Figura Los vértices son: 𝐴(0,0),𝐵(6.000,3.000),𝐶(7.000,3.000),𝐷(8.000,2.000).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(0,0)=0,𝐹(𝐵)=𝐹(6.000,3.000)=390.000,𝐹(𝐶)=𝐹(7.000,3.000)=430.000,𝐹(𝐷)=𝐹(8.000,2.000)=420.000. Por tanto, el valor máximo de los beneficios se alcanza con 7.000 aficionados del equipo local y 3.000 del equipo visitante, con un importe de 430.000€.

Ejercicio 2

  1. Se considera la matriz 𝐴=⎛⎜ ⎜ ⎜⎝1−100𝑚−21𝑚4⎞⎟ ⎟ ⎟⎠.
    1. Obtenga para qué valores de 𝑚 la matriz 𝐴 tiene inversa.
    2. Calcule, en caso de existir, la inversa de 𝐴 para 𝑚 =1.
  2. Despeje y simplifique 𝑋 en la ecuación 𝑋𝐵 −𝐵2 +𝐵 =0, sabiendo que la matriz 𝐵 es invertible.

Resolución
    1. Calculamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣1−100𝑚−21𝑚4∣=4𝑚+2+2𝑚=6𝑚+2. La inversa de 𝐴 existe si y solo si su determinante es no nulo. |𝐴|=0⇔6𝑚+2=0⇔𝑚=−13. Por tanto, la matriz 𝐴 tiene inversa si 𝑚 ≠ −13.
    2. Si 𝑚 =1, por el apartado anterior 𝐴 es invertible con det(𝐴) =8. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝6−2−144−2221⎞⎟ ⎟ ⎟⎠. Calculamos su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=18⎛⎜ ⎜ ⎜⎝642−242−1−21⎞⎟ ⎟ ⎟⎠.
  2. Despejamos 𝑋 en la ecuación matricial. 𝑋𝐵−𝐵2+𝐵=0⇔(𝑋−𝐵+𝐼)𝐵=0⇔𝑋−𝐵+𝐼=0⇔𝑋=𝐵+𝐼.

Ejercicio 3

  1. Se considera la función 𝑓(𝑥)={𝑎𝑥2+𝑏𝑥+6,si 𝑥≤2,5,−1,4𝑥+7,si 𝑥>2,5, con 𝑎 y 𝑏 números reales. Calcule el valor de los parámetros 𝑎 y 𝑏 para que la función sea continua y tenga un máximo en 𝑥 =1.
  2. Represente gráficamente la función 𝑔(𝑥) = −2𝑥2 +2𝑥 +4 y calcule el área de la región acotada, limitada por la gráfica de dicha función y el eje de abscisas.

Resolución
    • Si 𝑥 ≠2,5, 𝑓 es continua y derivable con 𝑓′(𝑥)={2𝑎𝑥+𝑏,si 𝑥<2,5,−1,4,si 𝑥>2,5.
    • Estudiamos la continuidad para el punto de ruptura 𝑥 =2,5. lím𝑥→2,5−⁡𝑓(𝑥)=lím𝑥→2,5−⁡(𝑎𝑥2+𝑏𝑥+6)=6,25𝑎+2,5𝑏+6,lím𝑥→2,5+⁡𝑓(𝑥)=lím𝑥→2,5+⁡(−1,4𝑥+7)=3,5,𝑓(2,5)=6,25𝑎+2,5𝑏+6. Para que 𝑓 sea continua, ha de verificarse 6,25𝑎+2,5𝑏+6=3,5⇔6,25𝑎+2,5𝑏=−2,5⇔25𝑎+10𝑏=−10⇔5𝑎+2𝑏=−2.
    Además, para que 𝑓 tenga un máximo en 𝑥 =1 ha de ocurrir que 𝑓′(1) =0. 𝑓′(1)=0⇔2𝑎+𝑏=0. Con estas dos condiciones, planteamos el sistema de ecuaciones {5𝑎+2𝑏=−2,2𝑎+𝑏=0. Resolvemos el sistema por sustitución. Como 2𝑎 +𝑏 =0 ⇔𝑏 = −2𝑎, 5𝑎+2𝑏=−2𝑏=−2𝑎←←←←←←←←→5𝑎−4𝑎=−2⇔𝑎=−2. Así que 𝑏=−2𝑎𝑎=−2←←←←←←←→𝑏=4. Por tanto, 𝑎 = −2 y 𝑏 =4.
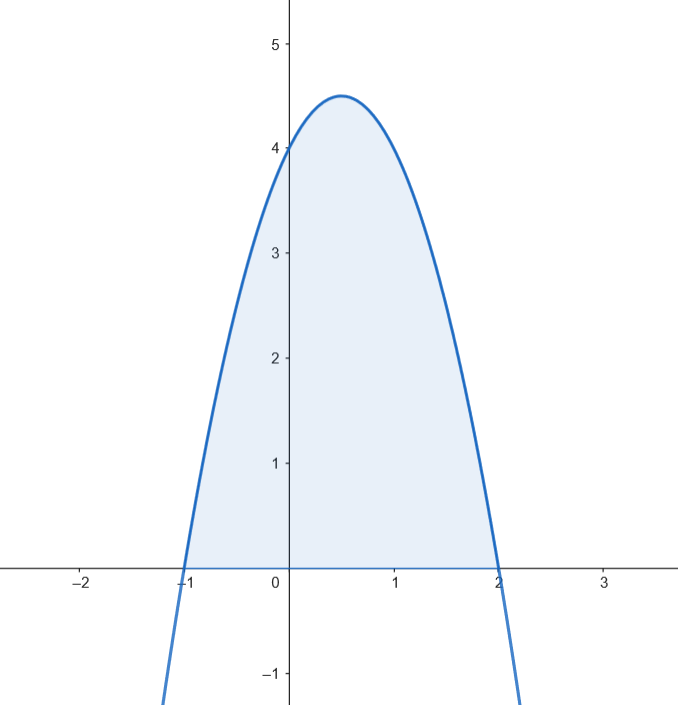  2. En primer lugar, hallamos los puntos de corte de la función 𝑔 con el eje 𝑋. 𝑔(𝑥)=0⇔−2𝑥2+2𝑥+4=0⇔𝑥2−𝑥−2=0⇔{𝑥=−1,𝑥=2. Así que los puntos de corte son ( −1,0) y (2,0). Además, observamos que 𝑔 es una parábola con vértice (12,92). Representamos la función y el recinto acotado. Figura Calculamos el área del recinto. ∫2−1𝑔(𝑥)𝑑𝑥=∫2−1(−2𝑥2+2𝑥+4)𝑑𝑥=[−23𝑥3+𝑥2+4𝑥]2−1=−163+4+8−(23+1−4)=9𝑢2.

Ejercicio 4

Se considera la función 𝑓(𝑥)=⎧{ { {⎨{ { {⎩𝑥23,si 0≤𝑥≤2,4𝑥+1,si 𝑥>2.

  1. Estudie la continuidad y derivabilidad de la función 𝑓.
  2. Determine los intervalos de crecimiento y decrecimiento, el máximo de la función y represente gráficamente la función 𝑓.

Resolución
    • Si 𝑥 ≥0 y 𝑥 ≠2, 𝑓 es continua y derivable con 𝑓′(𝑥)=⎧{ {⎨{ {⎩23𝑥,si 0≤𝑥<2,−4(𝑥+1)2,si 𝑥>2.
    • Estudiamos la continuidad para el punto de ruptura 𝑥 =2. lím𝑥→2−⁡𝑓(𝑥)=lím𝑥→2−⁡𝑥23=43,lím𝑥→2+⁡𝑓(𝑥)=lím𝑥→2+⁡4𝑥+1=43,𝑓(2)=43. Observamos que lím𝑥→2−⁡𝑓(𝑥)=lím𝑥→2+⁡𝑓(𝑥)=𝑓(2). Así que 𝑓 es continua en 𝑥 =2.
      Pasamos a estudiar la derivabilidad. 𝑓′−(2)=lím𝑥→2−⁡𝑓′(𝑥)=lím𝑥→2−⁡23𝑥=43,𝑓′+(2)=lím𝑥→2+⁡𝑓′(𝑥)=lím𝑥→2+−4(𝑥+1)2=−49. Observamos que 𝑓′−(2) ≠𝑓′+(2), así que 𝑓 no es derivable en 𝑥 =2.
    Por tanto, 𝑓 es continua en [0, +∞) y derivable en [0,2) ∪(2, +∞).

  2. Para hallar los puntos críticos, igualamos las dos ramas de la derivada a cero.

    • Si 0 ≤𝑥 <2, 𝑓(𝑥)=0⇔23𝑥=0⇔𝑥=0.
    • Si 𝑥 >2, 𝑓′(𝑥)=−4(𝑥+1)2≠0.

    Así que el único punto crítico es 𝑥 =0. También consideramos 𝑥 =2 por ser el punto de ruptura. Estudiemos el signo de la derivada.

    (0,2) (2, +∞)
    signo de 𝑓′ + −
    monotonía de 𝑓 → →

    Por tanto, 𝑓 es creciente en (0,2) y es decreciente en (2, +∞). Además, el punto (2,43) es un máximo relativo.

    Representamos gráficamente la función usando la información obtenida.

    Figura

Ejercicio 5

Durante la pasada temporada, una tenista ganó el 90% de los partidos que jugó sobre tierra y la mitad cuando lo hizo sobre otro tipo de superficie. De los 40 partidos que jugó la temporada pasada, 25 lo hizo sobre tierra. Elegido al azar un partido de la temporada pasada de esta tenista, halle la probabilidad de que:

  1. Ganase el partido.
  2. No ganase sabiendo que jugó sobre tierra.
  3. Jugase sobre tierra sabiendo que ganó.

Resolución

Llamamos 𝑇 a jugar sobre tierra y 𝐺 a ganar. Podemos hacer un diagrama de árbol.

𝐺
0,9←←←←←←←←←←→
𝑇
0,625←←←←←←←←←←←←→ 0,1←←←←←←←←←←→
𝐺𝑐
𝐺
0,375←←←←←←←←←←←←→ 0,5←←←←←←←←←←→
𝑇𝑐
0,5←←←←←←←←←←→
𝐺𝑐
  1. Por el teorema de la probabilidad total, la probabilidad de que ganase el partido es: 𝑃(𝐺)=𝑃(𝐺∩𝑇)+𝑃(𝐺∩𝑇𝑐)=𝑃(𝑇)⋅𝑃(𝐺|𝑇)+𝑃(𝑇𝑐)⋅𝑃(𝐺|𝑇𝑐)=0,625⋅0,9+0,375⋅0,5=0,75.
  2. La probabilidad de que no ganase sabiendo que jugó sobre tierra es 𝑃(𝐺𝑐|𝑇) =0,1.
  3. La probabilidad de que jugase sobre tierra sabiendo que ganó es: 𝑃(𝑇|𝐺)=𝑃(𝑇∩𝐺)𝑃(𝐺)=𝑃(𝑇)⋅𝑃(𝐺|𝑇)𝑃(𝐺)=0,625⋅0,90,75=0,75.

Ejercicio 6

El 32% de las microempresas tiene página web y el 64,6% ni tiene página web ni realiza ventas por comercio electrónico. De las microempresas que tienen página web, el 30% realiza ventas por comercio electrónico. Se selecciona al azar una microempresa.

  1. Calcule la probabilidad de que tenga página web o realice ventas por comercio electrónico.
  2. Calcule la probabilidad de que realice ventas por comercio electrónico.
  3. Calcule la probabilidad de que no tenga página web y realice ventas por comercio electrónico.
  4. Razone si son independientes los sucesos "Tener página web" y "Realizar ventas por comercio electrónico". ¿Son incompatibles?

Resolución

Llamamos 𝑊 a tener página web y 𝑉 a realizar ventas por comercio electrónico. Sabemos que: 𝑃(𝑊)=0,32,𝑃(𝑊𝑐∩𝑉𝑐)=0,646y𝑃(𝑉|𝑊)=0,3.

  1. La probabilidad de tener página web o realizar ventas por comercio electrónico es: 𝑃(𝑊∪𝑉)=1−𝑃(𝑊𝑐∩𝑉𝑐)=1−0,646=0,354.
  2. Sabemos que la probabilidad de tener página web o realizar ventas por comercio electrónico viene dada por: 𝑃(𝑊∪𝑉)=𝑃(𝑊)+𝑃(𝑉)−𝑃(𝑊∩𝑉). Además, sabemos que: 𝑃(𝑊∩𝑉)=𝑃(𝑊)⋅𝑃(𝑉|𝑊)=0,32⋅0,3=0,096. Así que, despejando en la expresión anterior, la probabilidad de realizar ventas por comercio electrónico es: 𝑃(𝑉)=𝑃(𝑊∪𝑉)−𝑃(𝑊)+𝑃(𝑊∩𝑉)=0,354−0,32+0,096=0,13.
  3. La probabilidad de no tener página web y realizar ventas por comercio electrónico es: 𝑃(𝑊𝑐∩𝑉)=𝑃(𝑉)−𝑃(𝑊∩𝑉)=0,13−0,096=0,034.
  4. Como 𝑃(𝑉) ≠𝑃(𝑉|𝑊), los sucesos 𝑊 y 𝑉 no son independientes. Por otro lado, como 𝑃(𝑊 ∩𝑉) >0, los sucesos no son incompatibles.

Ejercicio 7

El peso de la gamba roja de Garrucha, en gramos, sigue una distribución Normal de media poblacional desconocida y desviación típica 5 gramos.

  1. Se elige una muestra aleatoria de 100 gambas obteniéndose una media de 53 gramos. Calcule un intervalo de confianza al 97,5% para estimar el peso medio de la gamba roja.
  2. Sabiendo que la media poblacional es 53 gramos y escogiendo una muestra aleatoria de 64 gambas, calcule la probabilidad de que el peso medio de la muestra sea superior a 53,25 gramos.

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Como el nivel de confianza es del 97,5%, entonces: 𝛼=1−0,975=0,025⇒1−𝛼2=1−0,0252=0,9875⇒𝑧𝛼/2=2,24. Por tanto, el intervalo de confianza para estimar el peso medio de la gamba roja en gramos con un nivel de confianza del 97,5% es: 𝐼=(53−2,24⋅5√100,53+2,24⋅5√100)=(51,88;54,12).
  2. La distribución de las medias muestrales ――𝑋 sigue una normal 𝑁(𝜇,𝜎√𝑛) con 𝜇 =53, 𝜎 =5 y 𝑛 =64. Es decir, ――𝑋 ∼𝑁(53; 0,625). La probabilidad de que el peso medio de la muestra sea superior a 53,25 es: 𝑃(――𝑋>53,25)=𝑃(𝑍>53,25−530,625)=𝑃(𝑍>0,4)=1−𝑃(𝑍≤0,4)=0,3446.

Ejercicio 8

Se desea estimar la proporcion de clientes de una compañía de seguros que han requerido el servicio de asistencia en carretera. Para ello, se ha recogido una muestra aleatoria de 300 asegurados resultando que 90 han requerido este servicio.

  1. Obtenga un intervalo de confianza al 97% para estimar la proporción de asegurados que han solicitado este servicio.
  2. Con la proporción muestral facilitada y con un nivel de confianza del 95%, ¿cuál es el número mínimo de asegurados que se deberán seleccionar aleatoriamente para que la proporción muestral y la poblacional no difieran en más de un 3%?

Resolución
  1. Como 90 asegurados de 𝑛 =300 han requerido el servicio de asistencia en carretera, la proporción muestral es: 𝑝=90300=0,3. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar la proporción de asegurados que ha solicitado el servicio con un nivel de confianza del 97% es: 𝐼=(0,3−2,17⋅√0,3⋅(1−0,3)300,0,3+2,17⋅√0,3⋅(1−0,3)300)≈(0,2426;0,3574).
  2. Si el nivel de confianza es del 95%, entonces: 𝛼=1−0,95=0,05⇒1−𝛼2=1−0,052=0,975⇒𝑧𝛼/2=1,96. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=1,96⋅√0,3⋅(1−0,3)𝑛=1,96⋅√0,21𝑛. Si se quiere el error no sea mayor que 0,03, entonces: 1,96⋅√0,21𝑛=0,03⇔√0,21𝑛=0,031,96⇔0,21𝑛=0,0321,962⇔𝑛=0,21⋅1,9620,032≈896,3733. Por tanto, el número mínimo de asegurados de la muestra debe ser 897.