Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 4 de 2023

Ejercicio 1

Una empresa de pinturas quiere elaborar botes de pintura de dos colores nuevos: Júpiter y Minerva. Para ello, dispone de 1.000 kg de pintura de color verde, 800 kg de color morado y 300 kg de color naranja. Para elaborar un bote de color Júpiter se necesitan 10 kg de pintura verde, 5 kg de morada y 5 kg de naranja. Para elaborar un bote de color Minerva se necesitan 5 kg de pintura verde y 5 kg de morada. Sabiendo que se obtiene un beneficio de 30€ por cada bote de pintura Júpiter y 20€ por un bote de pintura Minerva, ¿cuántos botes de cada tipo deberá fabricar la empresa para obtener un beneficio máximo? ¿Cuál será el valor de ese beneficio?

Resolución

Llamamos 𝑥 al número de botes de pintura de color Júpiter e 𝑦 al de Minerva. Podemos organizar la información en una tabla.

Verde (kg) Morado (kg) Naranja (kg) Beneficio (€)
Júpiter 10 5 5 30
Minerva 5 5 0 20
Total 1.000 800 300

Las restricciones del problema son: ⎧{ { { {⎨{ { { {⎩10𝑥+5𝑦≤1.000,5𝑥+5𝑦≤800,5𝑥≤300,𝑥≥0,𝑦≥0.⇔⎧{ { { {⎨{ { { {⎩2𝑥+𝑦≤200,𝑥+𝑦≤160,𝑥≤60,𝑥≥0,𝑦≥0. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=30𝑥+20𝑦.

Representamos la región factible. 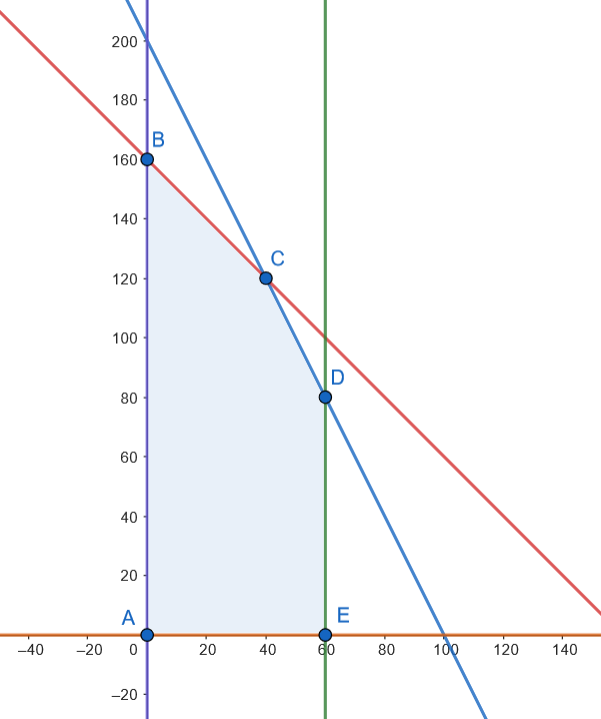Figura Los vértices son: 𝐴(0,0),𝐵(0,160),𝐶(40,120),𝐷(60,80)y𝐸(60,0).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(0,0)=0,𝐹(𝐵)=𝐹(0,160)=3.200,𝐹(𝐶)=𝐹(40,120)=3.600,𝐹(𝐷)=𝐹(60,80)=3.400,𝐹(𝐸)=𝐹(60,0)=1.800. Por tanto, el valor máximo de los beneficios se alcanza fabricando 40 botes de pintura de color Júpiter y 120 de Minerva, con unas ganancias de 3.600€.

Ejercicio 2

Se consideran las matrices 𝐴=⎛⎜ ⎜ ⎜⎝5−7670403−1⎞⎟ ⎟ ⎟⎠,𝐵=⎛⎜ ⎜ ⎜⎝12−9−201104−7⎞⎟ ⎟ ⎟⎠y𝐶=⎛⎜ ⎜ ⎜⎝12−1⎞⎟ ⎟ ⎟⎠.

  1. Halle las dimensiones de las siguientes matrices: 𝐶𝑡𝐴𝐶, 𝐴𝐶𝐶𝑡𝐵.
  2. Calcule, en caso de existir, las inversas de las matrices 𝐴 y 𝐵.
  3. Resuelva el siguiente sistema matricial: {2𝑋+3𝑌=𝐴,−3𝑋+4𝑌=𝐵.

Resolución
    • 𝐶𝑡 es de dimensión 1 ×3 y 𝐴 es 3 ×3, así que 𝐶𝑡𝐴 es de dimensión 1 ×3. Como 𝐶 es 3 ×1, la matriz 𝐶𝑡𝐴𝐶 es de dimensión 1 ×1.
    • 𝐴 es de dimensión 3 ×3 y 𝐶 es 3 ×1, así que 𝐴𝐶 es de dimensión 3 ×1. Como 𝐶𝑡 es 1 ×3, 𝐴𝐶𝐶𝑡 es de dimensión 3 ×3. Por último, como 𝐵 es 3 ×3, la matriz 𝐴𝐶𝐶𝑡𝐵 es de dimensión 3 ×3.
    • Hallamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣5−7670403−1∣=126−49−60=17. Como det(𝐴) ≠0, la matriz 𝐴 es invertible. Para hallar su inversa, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝−1272111−5−15−282249⎞⎟ ⎟ ⎟⎠. Calculamos su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=117⎛⎜ ⎜ ⎜⎝−1211−287−52221−1549⎞⎟ ⎟ ⎟⎠.
    • Hallamos en primer lugar el determinante de la matriz 𝐵. |𝐵|=∣12−9−201104−7∣=72−44−28=0. Como det(𝐵) =0, 𝐵 no es invertible.
  3. Resolvemos el sistema por reducción para evitar arrastrar fracciones. Multiplicamos la primera ecuación por 3 y la segunda por 2. {2𝑋+3𝑌=𝐴,−3𝑋+4𝑌=𝐵⇒{6𝑋+9𝑌=3𝐴,−6𝑋+8𝑌=2𝐵. Si sumamos ambas ecuaciones, obtenemos que 17𝑌=3𝐴+2𝐵⇔𝑌=117⎡⎢ ⎢⎣⎛⎜ ⎜ ⎜⎝15−21182101209−3⎞⎟ ⎟ ⎟⎠+⎛⎜ ⎜ ⎜⎝24−18−402208−14⎞⎟ ⎟ ⎟⎠⎤⎥ ⎥⎦=117⎛⎜ ⎜ ⎜⎝17−17017034017−17⎞⎟ ⎟ ⎟⎠==⎛⎜ ⎜ ⎜⎝1−1010201−1⎞⎟ ⎟ ⎟⎠. Sustituyendo en la primera ecuación, 2𝑋+3𝑌=𝐴⇔𝑋=12(𝐴−3𝑌)=12⎡⎢ ⎢⎣⎛⎜ ⎜ ⎜⎝5−7670403−1⎞⎟ ⎟ ⎟⎠−⎛⎜ ⎜ ⎜⎝3−3030603−3⎞⎟ ⎟ ⎟⎠⎤⎥ ⎥⎦=12⎛⎜ ⎜ ⎜⎝2−4640−2002⎞⎟ ⎟ ⎟⎠==⎛⎜ ⎜ ⎜⎝1−2320−1001⎞⎟ ⎟ ⎟⎠. Por tanto, 𝑋=⎛⎜ ⎜ ⎜⎝1−2320−1001⎞⎟ ⎟ ⎟⎠e𝑌=⎛⎜ ⎜ ⎜⎝1−1010201−1⎞⎟ ⎟ ⎟⎠.

Ejercicio 3

Se considera la función 𝑓(𝑥)={𝑥2−4𝑥+4,si 𝑥<3,−𝑥+4,si 𝑥≥3.

  1. Estudie la continuidad y derivabilidad de la función 𝑓 en todos los puntos de su dominio.
  2. Respresente gráficamente 𝑓.
  3. Calcule el área de la región limitada por la gráfica de 𝑓, el eje de abscisas y las rectas 𝑥 =2 y 𝑥 =4.

Resolución
    • Si 𝑥 ≠3, 𝑓 es continua y derivable con 𝑓′(𝑥)={2𝑥−4,si 𝑥<3,−1,si 𝑥>3.
    • Estudiamos la continuidad para el punto de ruptura 𝑥 =3. lím𝑥→3−⁡𝑓(𝑥)=lím𝑥→3−⁡(𝑥2−4𝑥+4)=1,lím𝑥→3+⁡𝑓(𝑥)=lím𝑥→3+⁡(−𝑥+4)=1,𝑓(3)=1. Observamos que lím𝑥→3−⁡𝑓(𝑥)=lím𝑥→3+⁡𝑓(𝑥)=𝑓(3). Así que 𝑓 es continua en 𝑥 =3.
      Pasamos a estudiar la derivabilidad. 𝑓′−(3)=lím𝑥→3−⁡𝑓′(𝑥)=lím𝑥→3−⁡(2𝑥−4)=2,𝑓′+(3)=lím𝑥→3+⁡𝑓′(𝑥)=lím𝑥→3+−1=−1. Observamos que 𝑓′−(3) ≠𝑓′+(3), así que 𝑓 no es derivable en 𝑥 =3.
    Por tanto, 𝑓 es continua en ℝ y derivable en ℝ ∖{3}.
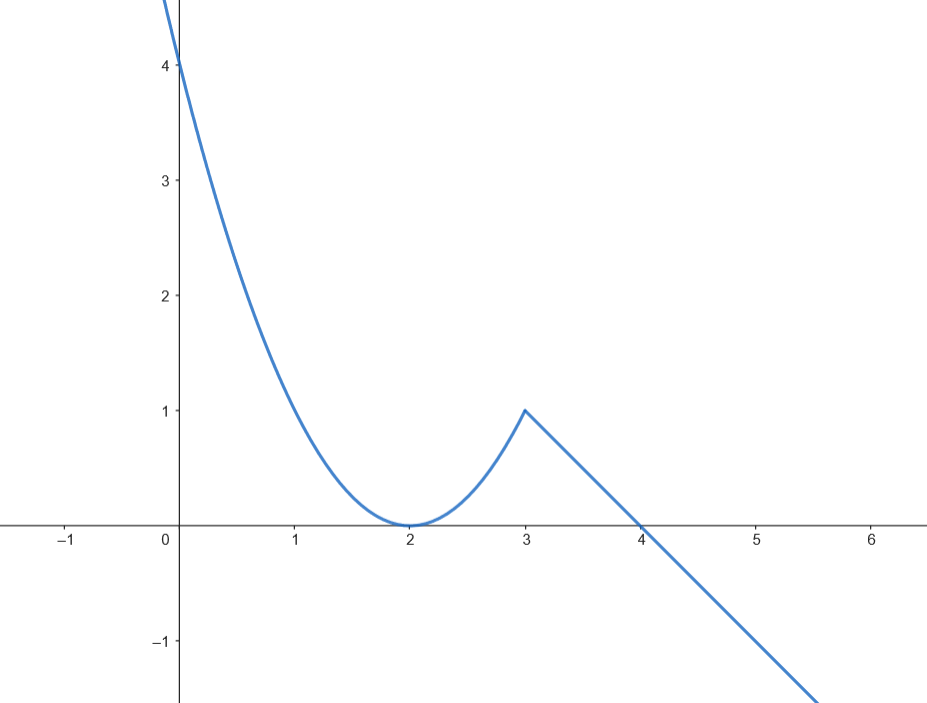
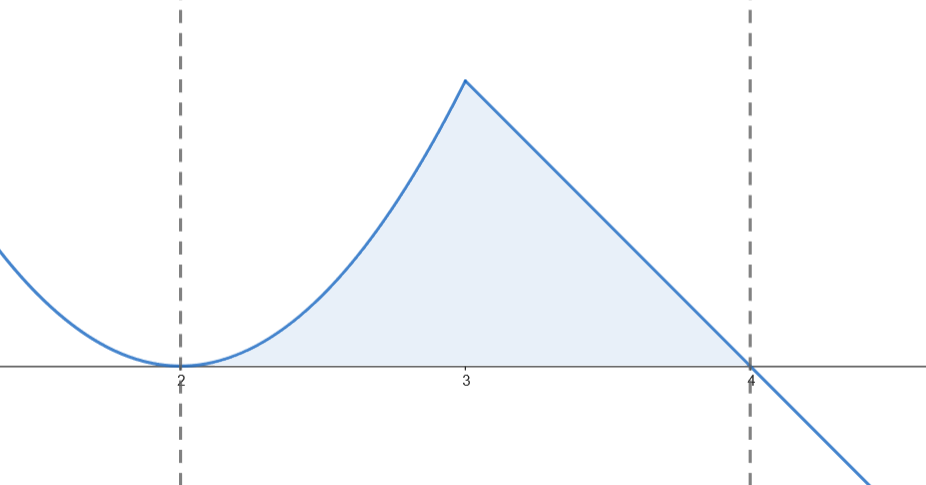  2. Representamos gráficamente la función. Observamos que la parábola tiene vértice (2,0). Figura
  3. Podemos representar el recinto acotado limitado por la gráfica de 𝑓 y las rectas 𝑥 =2 y 𝑥 =4. Figura Calculamos el área. ∫32(𝑥2−4𝑥+4)𝑑𝑥+∫43(−𝑥+4)𝑑𝑥=[13𝑥3−2𝑥2+4𝑥]32+[−12𝑥2+4𝑥]43==9−18+12−(83−8+8)−8+16−(−92+12)=56𝑢2.

Ejercicio 4

La función 𝐵(𝑡) = −𝑡2 +21𝑡 −20 con 0 ≤𝑡 ≤15 representa el beneficio, en miles de euros, de una empresa en función de los años, 𝑡.

  1. Si la función 𝐼(𝑡) = −𝑡2 +48𝑡 representa los ingresos de esta empresa, en miles de euros, para el mismo intervalo de tiempo, ¿cuál es la función de gastos de dicha empresa? ¿Cuáles son los gastos iniciales?
  2. Calcule el momento a partir del cual el beneficio fue positivo.
  3. Calcule en qué momento el beneficio fue máximo y el valor del mismo.
  4. Represente gráficamente la función beneficio.

Resolución
  1. Los gastos vienen dados por la diferencia entre los ingresos y el beneficio. La función que representa los gastos en miles de euros en función de los años es: 𝐺(𝑡)=𝐼(𝑡)−𝐵(𝑡)=−𝑡2+48𝑡−(−𝑡2+21𝑡−20)=27𝑡+20. Como 𝐺(0) =20, los gastos iniciales son 20.000€.
  2. Hallamos los puntos de corte de 𝐵 con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝐵(𝑡)=0⇔−𝑡2+21𝑡−20=0⇔{𝑡=1,𝑡=20. Así que el único punto de corte con el eje en el dominio [0,15] está en 𝑡 =1. Observamos además que 𝐵(𝑡) >0 para 1 <𝑡 ≤15. Por tanto, el beneficio es positivo a partir del primer año.
  3. Como la función 𝐵 es una parábola cóncava, su máximo se alcanza en el vértice (10,5; 90,25). Es decir, el beneficio máximo se alcanza a los diez años y medio, con un valor de 90.250€.
  4. Representamos gráficamente la función usando la información del apartado anterior. Figura

Ejercicio 5

Una fábrica produce procesadores que se clasifican en un primer control en tres tipos, A, B y C, según la frecuencia a la que pueden trabajar. El 60% de los procesadores fabricados se clasifican de tipo A, el 30% de tipo B y el resto de tipo C. En un segundo control, se desechan el 20% de los procesadores de tipo A, el 50% de los de tipo B y el 60% de los de tipo C, por problemas al trabajar a ciertas temperaturas. Si se elige un procesador de esta fábrica al azar, calcule la probabilidad de que:

  1. Sea descartado y sea de tipo A o de tipo B.
  2. Sea descartado.
  3. Sea de tipo C sabiendo que no ha sido descartado.

Resolución

Llamamos 𝐴 a ser de tipo A, 𝐵 a ser de tipo B, 𝐶 a ser de tipo C y 𝐷 a descartar el procesador. Podemos hacer un diagrama de árbol.

𝐷
0,2←←←←←←←←←←→
𝐴
0,6←←←←←←←←←←→ 0,8←←←←←←←←←←→
𝐷𝑐
𝐷
0,5←←←←←←←←←←→
0,3←←←←←←←←←←→ 𝐵
0,5←←←←←←←←←←→
𝐷𝑐
𝐷
0,1←←←←←←←←←←→ 0,6←←←←←←←←←←→
𝐶
0,4←←←←←←←←←←→
𝐷𝑐
  1. La probabilidad de que un procesador sea descartado y sea de tipo A o B es: 𝑃(𝐷∩(𝐴∪𝐵))=𝑃((𝐷∩𝐴)∪(𝐷∩𝐵))=𝑃(𝐷∩𝐴)+𝑃(𝐷∩𝐵)=𝑃(𝐴)⋅𝑃(𝐷|𝐴)+𝑃(𝐵)⋅𝑃(𝐷|𝐵)==0,6⋅0,2+0,3⋅0,5=0,27.
  2. Por el teorema de la probabilidad total, la probabilidad de que un procesador sea descartado es: 𝑃(𝐷)=𝑃(𝐷∩𝐴)+𝑃(𝐷∩𝐵)+𝑃(𝐷∩𝐶)=𝑃(𝐴)⋅𝑃(𝐷|𝐴)+𝑃(𝐵)⋅𝑃(𝐷|𝐵)+𝑃(𝐶)⋅𝑃(𝐷|𝐶)==0,27+0,1⋅0,6=0,33.
  3. La probabilidad de que un procesador sea de tipo C sabiendo que no ha sido descartado es: 𝑃(𝐶|𝐷𝑐)=𝑃(𝐶∩𝐷𝑐)𝑃(𝐷𝑐)=𝑃(𝐶)−𝑃(𝐶∩𝐷)1−𝑃(𝐷)=𝑃(𝐶)−𝑃(𝐶)⋅𝑃(𝐷|𝐶)1−𝑃(𝐷)=0,1−0,1⋅0,61−0,33≈0,0597.

Ejercicio 6

El 75% del alumnado de un instituto utiliza la plataforma del centro como medio para comunicarse con sus profesores y el 40% lo hace a través del correo electrónico. Además, hay un 15% que no usa ninguno de estos medios. Se elige un estudiante de este instituto al azar.

  1. Calcule la probabilidad de que utilice ambos medios de comunicación.
  2. Calcule la probabilidad de que utilice solamente uno de estos medios de comunicación.
  3. Calcule la probabilidad de que utilice la plataforma del centro sabiendo que no usa el correo electrónico como medio de comunicación.
  4. Razone si los sucesos "Utilizar la plataforma del centro" y "Utilizar el correo electrónico" son independientes.

Resolución

Llamamos 𝐴 a usar la plataforma del centro y 𝐵 a usar el correo electrónico. Sabemos que: 𝑃(𝐴)=0,75,𝑃(𝐵)=0,4y𝑃((𝐴∪𝐵)𝑐)=0,15⇒𝑃(𝐴∪𝐵)=0,85.

  1. La probabilidad de que un estudiante utilice ambos medios de comunicación es: 𝑃(𝐴∩𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∪𝐵)=0,75+0,4−0,85=0,3.
  2. La probabilidad de que un estudiante utilice solo uno de los dos medios de comunicación es: 𝑃(𝐴−𝐵)+𝑃(𝐵−𝐴)=𝑃(𝐴∪𝐵)−𝑃(𝐴∩𝐵)=0,85−0,3=0,55.
  3. La probabilidad de que un estudiante utilice la plataforma del centro sabiendo que no usa el correo electrónico es: 𝑃(𝐴|𝐵𝑐)=𝑃(𝐴∩𝐵𝑐)𝑃(𝐵𝑐)=𝑃(𝐴)−𝑃(𝐴∩𝐵)1−𝑃(𝐵)=0,75−0,31−0,4=0,75.
  4. Como 𝑃(𝐴) =𝑃(𝐴|𝐵𝑐), los sucesos 𝐴 y 𝐵 son independientes.

Ejercicio 7

Una empresa fabrica piezas cuyo diámetro sigue una distribución Normal de media desconocida y varianza 9 mm2.

  1. Se seleccionan al azar 144 piezas obteniéndose un diámetro medio de 81 mm. Determine un intervalo de confianza al 98,5% para estimar el diámetro medio de las piezas fabricadas por la empresa.
  2. Con el mismo nivel de confianza del apartado anterior, ¿de qué tamaño mínimo habría que tomar la muestra para obtener un intervalo de confianza con una amplitud máxima de 0,9?
  3. Suponiendo que la media poblacional es de 80,4 mm y tomando muestras aleatorias de 64 piezas, ¿qué distribución de probabilidad sigue la variable aleatoria diámetro medio muestral? ¿Cuál es la probabilidad de que el diámetro medio muestral esté comprendido entre 79,5 mm y 80,7 mm?

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Como el nivel de confianza es del 98,5%, entonces: 𝛼=1−0,985=0,015⇒1−𝛼2=1−0,0152=0,9925⇒𝑧𝛼/2=2,43. Por tanto, el intervalo de confianza para estimar el diámetro medio de las piezas con un nivel de confianza del 98,5% es: 𝐼=(81−2,43⋅√9√144,81+2,43⋅√9√144)≈(80,3925;81,6075).
  2. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=2,43⋅√9√𝑛=7,29√𝑛. Si se quiere que el intervalo de confianza tenga una amplitud máxima de 0,9, 𝐸=0,92=0,45. Así que: 7,29√𝑛=0,45⇔√𝑛=7,290,45⇔𝑛=7,2920,452=262,44. Por tanto, el tamaño mínimo de la muestra debe ser de 263 piezas.
  3. La distribución del diámetro medio muestral ――𝑋 sigue una normal 𝑁(𝜇,𝜎√𝑛) con 𝜇 =80,4, 𝜎 =√9 =3 y 𝑛 =64. Es decir, ――𝑋 ∼𝑁(80,4; 0,375). La probabilidad de que el diámetro medio muestral esté comprendido entre 79,5 mm y 80,7 mm es: 𝑃(79,5≤――𝑋≤80,7)=𝑃(79,5−80,40,375≤𝑍≤80,7−80,40,375)=𝑃(−2,4≤𝑍≤0,8)==𝑃(𝑍≤0,8)−𝑃(𝑍≤−2,4)=𝑃(𝑍≤0,8)−(1−𝑃(𝑍≤2,4))≈0,7799.

Ejercicio 8

Se selecciona una muestra aleatoria de 300 habitantes de una ciudad, a los que se les pregunta si creen que llevan una dieta saludable. De las personas encuestadas, 180 han contestado afirmativamente, mientras que el resto ha respondido que no.

  1. Calcule un intervalo de confianza al 95% para la proporción de personas que creen seguir una dieta saludable.
  2. ¿Cuál sería el número de habitantes mínimo necesario en este estudio de opinión para que se reduzca a un tercio del error cometido en el intervalo (0,54; 0,66) con el mismo nivel de confianza?

Resolución
  1. Como 180 personas de 𝑛 =300 creen que siguen una media saludable, la proporción muestral es: 𝑝=180300=0,6. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 95%, entonces: 𝛼=1−0,95=0,05⇒1−𝛼2=1−0,052=0,975⇒𝑧𝛼/2=1,96. Por tanto, el intervalo de confianza para estimar la proporción poblacional de personas que creen seguir una dieta saludable con un nivel de confianza del 95% es: 𝐼=(0,6−1,96⋅√0,6⋅(1−0,6)300,0,6+1,96⋅√0,6⋅(1−0,6)300)≈(0,5446;0,6554).
  2. En primer lugar, el error cometido en el intervalo (0,54; 0,66) es: 0,66−0,542=0,06. Por otro lado, el error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=1,96⋅√0,6⋅(1−0,6)𝑛=1,96⋅√0,24√𝑛. Si se quiere que el error máximo sea un tercio del error cometido en el intervalo dado, entonces: 1,96⋅√0,24√𝑛=13⋅0,06⇔1,96⋅√0,24√𝑛=0,02⇔√𝑛=1,96⋅√0,240,02⇔𝑛=1,962⋅0,240,022=2.304,96. Por tanto, el tamaño mínimo de la muestra debe ser de 2.305 habitantes.