Icono Matemáticas de Selectividad

Buscar GitHub

📋 Junio de 2022

Ejercicio 1

Una pastelería decide preparar dos tipos de cajas de pastelitos para regalar a los clientes en su inauguración. En total dispone de 120 piononos y 150 pestiños. En la caja del primer tipo habrá 3 piononos y 2 pestiños y en la del segundo tipo 4 piononos y 6 pestiños. Deben preparar al menos 9 cajas del segundo tipo. Determine cuántas cajas de cada tipo deberá preparar para realizar el máximo número de regalos posible. En este caso, indique cuántos piononos y cuántos pestiños se utilizarán.

Resolución

Llamamos 𝑥 al número de cajas del primer tipo e 𝑦 al del segundo tipo. Podemos organizar la información en una tabla.

Piononos Pestiños
Caja de tipo 1 3 2
Caja de tipo 2 4 6
Total 120 150

Las restricciones del problema son: ⎧{ { {⎨{ { {⎩3𝑥+4𝑦≤120,2𝑥+6𝑦≤150,𝑦≥9,𝑥≥0⇔⎧{ { {⎨{ { {⎩3𝑥+4𝑦≤120,𝑥+3𝑦≤75,𝑦≥9,𝑥≥0. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=𝑥+𝑦.

Representamos la región factible. 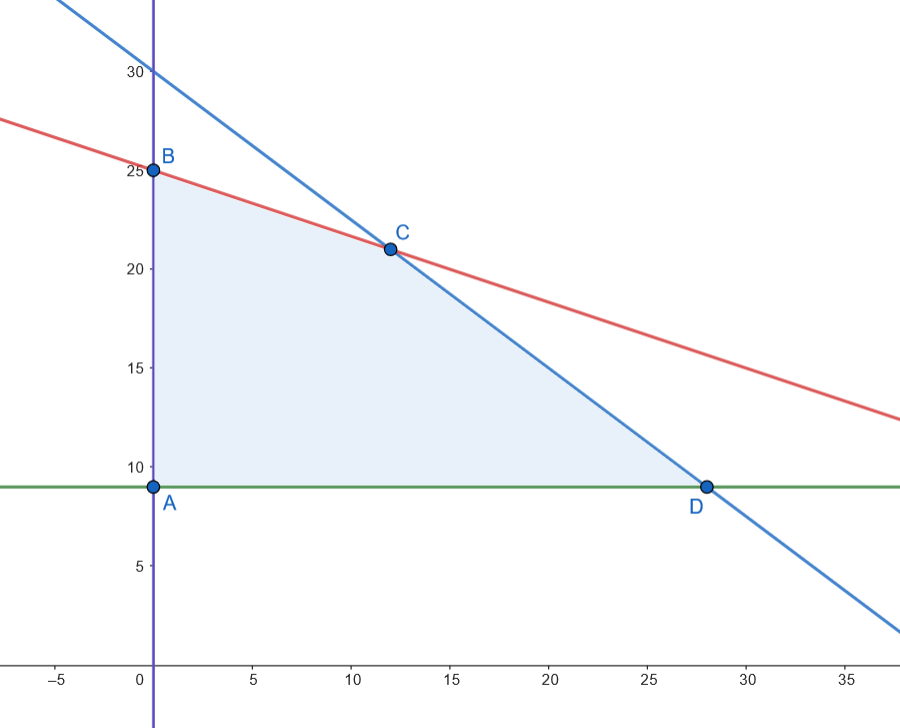Figura Los vértices son: 𝐴(0,9),𝐵(0,25),𝐶(12,21)y𝐷(28,9).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(0,9)=9,𝐹(𝐵)=𝐹(0,25)=25,𝐹(𝐶)=𝐹(12,21)=33,𝐹(𝐷)=𝐹(28,9)=37. Por tanto, el número máximo de regalos se alcanza preparando 28 cajas del primer tipo y 9 del segundo tipo. Se realizarán 28 ⋅3 +9 ⋅4 =120 piononos y 28 ⋅2 +9 ⋅6 =110 pestiños.

Ejercicio 2

Se consideran las matrices 𝐴=⎛⎜ ⎜ ⎜⎝𝑎100𝑎1341⎞⎟ ⎟ ⎟⎠,𝐵=(2−10)y𝐶=(13−1), donde 𝑎 es un número real.

  1. Halle los valores del parámetro 𝑎 para que la matriz 𝐴 tenga inversa.
  2. Para 𝑎 =2, calcule la matriz inversa de 𝐴.
  3. Para 𝑎 =2, resuelva la ecuación matricial 𝑋𝐴 +𝐼3 =𝐵𝑡𝐶.

Resolución
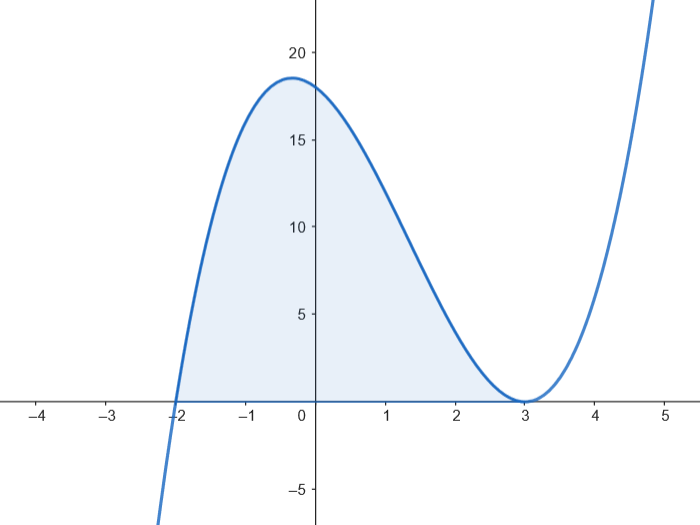  1. Calculamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣𝑎100𝑎1341∣=𝑎2+3−4𝑎=𝑎2−4𝑎+3. La inversa de 𝐴 existe si y solo si su determinante es no nulo. |𝐴|=0⇔𝑎2−4𝑎+3=0⇔{𝑎=1,𝑎=3. Por tanto, la matriz 𝐴 tiene inversa si 𝑎 ≠1 y 𝑎 ≠3.
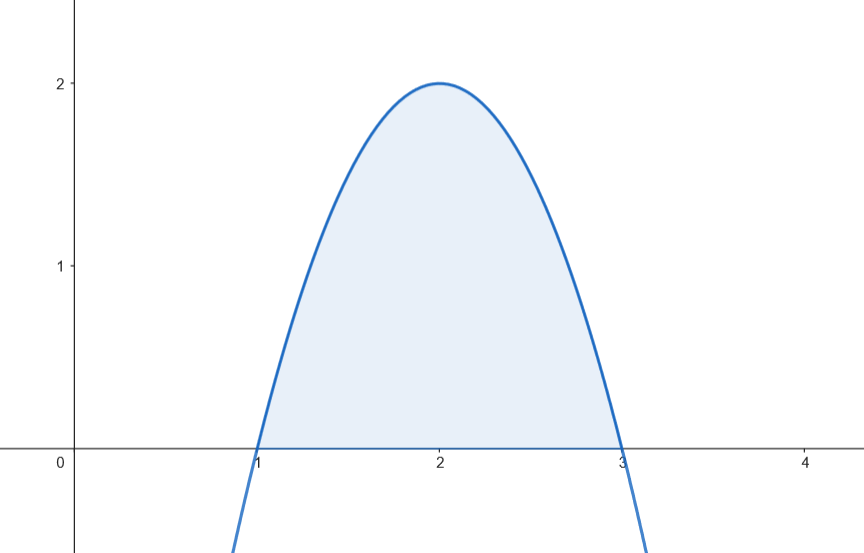  2. Si 𝑎 =2, por el apartado anterior 𝐴 es invertible con det(𝐴) = −1. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝−23−6−12−51−24⎞⎟ ⎟ ⎟⎠. Calculamos su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=−⎛⎜ ⎜ ⎜⎝−2−1132−2−6−54⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝21−1−3−2265−4⎞⎟ ⎟ ⎟⎠.
  3. Resolvemos la ecuación matricial. 𝑋𝐴+𝐼3=𝐵𝑡𝐶⇔𝑋𝐴=𝐵𝑡𝐶−𝐼3⇔𝑋=(𝐵𝑡𝐶−𝐼3)𝐴−1. Calculamos la matriz 𝑋 operando. 𝑋=(𝐵𝑡𝐶−𝐼3)𝐴−1=⎡⎢ ⎢⎣⎛⎜ ⎜ ⎜⎝2−10⎞⎟ ⎟ ⎟⎠(13−1)−⎛⎜ ⎜ ⎜⎝100010001⎞⎟ ⎟ ⎟⎠⎤⎥ ⎥⎦⎛⎜ ⎜ ⎜⎝21−1−3−2265−4⎞⎟ ⎟ ⎟⎠==⎡⎢ ⎢⎣⎛⎜ ⎜ ⎜⎝26−2−1−31000⎞⎟ ⎟ ⎟⎠−⎛⎜ ⎜ ⎜⎝100010001⎞⎟ ⎟ ⎟⎠⎤⎥ ⎥⎦⎛⎜ ⎜ ⎜⎝21−1−3−2265−4⎞⎟ ⎟ ⎟⎠==⎛⎜ ⎜ ⎜⎝16−2−1−4100−1⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝21−1−3−2265−4⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝−28−21191612−11−6−54⎞⎟ ⎟ ⎟⎠.

Ejercicio 3

  1. Se considera la función 𝑓(𝑥) =𝑥3 +𝑎𝑥2 +𝑏𝑥 +𝑐, con 𝑎, 𝑏 y 𝑐 números reales. Calcule los valores 𝑎, 𝑏 y 𝑐 sabiendo que la gráfica de 𝑓 posee un extremo relativo en el punto de abscisa 𝑥 =3 y que la pendiente de la recta tangente a la gráfica de 𝑓 en el punto 𝑃(0,18) es -3.
  2. Calcule el área del recinto acotado, limitado por la gráfica de la función 𝑔(𝑥) =𝑥3 −4𝑥2 −3𝑥 +18 y el eje de abscisas.

Resolución
  1. En primer lugar, hallamos la derivada de la función 𝑓. 𝑓′(𝑥)=3𝑥2+2𝑎𝑥+𝑏.
    • Si la función tiene un extremo en 𝑥 =3, entonces 𝑓′(3) =0. 𝑓′(3)=0⇔27+6𝑎+𝑏=0.
    • Si la pendiente de la recta tangente en 𝑥 =0 es -3, entonces 𝑓′(0) = −3. 𝑓′(0)=−3⇔𝑏=−3. Por otro lado, si (0,18) es un punto de la función, entonces 𝑓(0) =18. 𝑓(0)=18⇔𝑐=18.
    Despejando y sustituyendo en la primera ecuación, 27+6𝑎+𝑏=0⇔𝑎=−𝑏+276𝑏=−3←←←←←←←→𝑎=−4. Por tanto, 𝑎 = −4, 𝑏 = −3 y 𝑐 =18.
  2. En primer lugar, hallamos los puntos de corte de la función 𝑔 con el eje 𝑋. 𝑔(𝑥)=0⇔𝑥3−4𝑥2−3𝑥+18=0⇔(𝑥+2)(𝑥−3)2=0⇔{𝑥=−2,𝑥=3. Así que los puntos de corte son ( −2,0) y (3,0).
    Podemos representar el recinto acotado limitado por la gráfica de 𝑔 y el eje 𝑋. Figura Calculamos el área. ∫3−2𝑔(𝑥)𝑑𝑥=∫3−2(𝑥3−4𝑥2−3𝑥+18)𝑑𝑥=[14𝑥4−43𝑥3−32𝑥2+18𝑥]3−2==814−36−272+54−(4+323−6−36)=62512𝑢2.

Ejercicio 4

  1. Se considera la función 𝑓(𝑥)={6𝑥−3,si 𝑥≤1,𝑎𝑥2+𝑏𝑥+2,si 𝑥>1, con 𝑎 y 𝑏 números reales. Determine los valores de 𝑎 y 𝑏 para que 𝑓 sea continua y derivable en todo su dominio.
  2. Calcule el área del recinto acotado, limitado por el eje 𝑂𝑋 y la gráfica de la función 𝑔(𝑥) = −2𝑥2 +8𝑥 −6.

Resolución
    • Si 𝑥 ≠1, 𝑓 es continua y derivable con 𝑓′(𝑥)={6,si 𝑥<1,2𝑎𝑥+𝑏,si 𝑥>1.
    • Estudiamos la continuidad para el punto de ruptura 𝑥 =1. lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡(6𝑥−3)=3,lím𝑥→1+⁡𝑓(𝑥)=lím𝑥→1+⁡(𝑎𝑥2+𝑏𝑥+2)=𝑎+𝑏+2,𝑓(1)=3. Para que 𝑓 sea continua, ha de verificarse 𝑎+𝑏+2=3⇔𝑎+𝑏=1. Pasamos a estudiar la derivabilidad. 𝑓′−(1)=lím𝑥→1−⁡𝑓′(𝑥)=lím𝑥→1−⁡6=6,𝑓′+(1)=lím𝑥→1+⁡𝑓′(𝑥)=lím𝑥→1+⁡(2𝑎𝑥+𝑏)=2𝑎+𝑏. Para que 𝑓 sea derivable, ha de verificarse 2𝑎+𝑏=6.
    Con estas dos condiciones, planteamos el sistema de ecuaciones {𝑎+𝑏=1,2𝑎+𝑏=6. Resolvemos el sistema por reducción. Si restamos las ecuaciones, obtenemos que −𝑎=−5⇔𝑎=5. Sustituyendo en la primera ecuación, 𝑎+𝑏=1⇔𝑏=1−𝑎𝑎=5←←←←←←→𝑏=−4. Por tanto, 𝑎 =5 y 𝑏 = −4.
  2. En primer lugar, hallamos los puntos de corte de la función 𝑔 con el eje 𝑋. 𝑔(𝑥)=0⇔−2𝑥2+8𝑥−6=0⇔𝑥2−4𝑥+3=0⇔{𝑥=1,𝑥=3. Así que los puntos de corte son (1,0) y (3,0).
    Podemos representar el recinto acotado limitado por la gráfica de 𝑔 y el eje 𝑋. Figura Calculamos el área. ∫31𝑔(𝑥)𝑑𝑥=∫31(−2𝑥2+8𝑥−6)𝑑𝑥=[−23𝑥3+4𝑥2−6𝑥]31=−18+36−18−(−23+4−6)=83𝑢2.

Ejercicio 5

En un estudio realizado en una sucursal bancaria se ha determinado que el 70% de los créditos concedidos son hipotecarios y el 25% de los créditos superan los 200.000€. El 20% de los créditos son hipotecarios y de más de 200.000€. Se elige al azar un cliente al que le han concedido un crédito. Calcule la probabilidad de que:

  1. El crédito no sea hipotecario y no supere los 200.000€.
  2. Si su crédito no es hipotecario, este no supere los 200.000€.
  3. Si su crédito supera los 200.000€, que este no sea hipotecario.

Resolución

Llamamos 𝐻 a conceder un crédito hipotecario y 𝑆 a conceder un crédito superior a 200.000€. Sabemos que: 𝑃(𝐻)=0,7,𝑃(𝑆)=0,25y𝑃(𝐻∩𝑆)=0,2.

  1. La probabilidad de que el crédito sea hipotecario o superior a 200.000€ es: 𝑃(𝐻∪𝑆)=𝑃(𝐻)+𝑃(𝑆)−𝑃(𝐻∩𝑆)=0,7+0,25−0,2=0,75. Por tanto, la probabilidad de que el crédito no sea hipotecario y no supere los 200.000€ es: 𝑃(𝐻𝑐∩𝑆𝑐)=𝑃((𝐻∪𝑆)𝑐)=1−𝑃(𝐻∪𝑆)=1−0,75=0,25.
  2. La probabilidad de que el crédito no supere los 200.000€ sabiendo que es hipotecario es: 𝑃(𝑆𝑐|𝐻𝑐)=𝑃(𝑆𝑐∩𝐻𝑐)𝑃(𝐻𝑐)=𝑃((𝑆∪𝐻)𝑐)1−𝑃(𝐻)=1−𝑃(𝑆∪𝐻)1−𝑃(𝐻)=1−0,751−0,7≈0,8333.
  3. La probabilidad de que el crédito no sea hipotecario sabiendo que supera los 200.000€ es: 𝑃(𝐻𝑐|𝑆)=1−𝑃(𝐻|𝑆)=1−𝑃(𝐻∩𝑆)𝑃(𝑆)=1−0,20,25=0,2.

Ejercicio 6

En su tiempo libre, el 65% de los estudiantes de un centro educativo juega con videojuegos, el 45% lee libros y el 15% no hace ninguna de las dos cosas. Elegido al azar un estudiante de dicho centro, calcule la probabilidad de que:

  1. Juegue con videojuegos o lea libros.
  2. Juegue con videojuegos y no lea libros.
  3. Lea libros sabiendo que no juega con videojuegos.

Resolución

Llamamos 𝑉 a jugar con videojuegos y 𝐿 a leer libros. Sabemos que: 𝑃(𝑉)=0,65,𝑃(𝐿)=0,45y𝑃(𝑉𝑐∩𝐿𝑐)=0,15.

  1. Observamos que: 𝑃(𝑉𝑐∩𝐿𝑐)=𝑃((𝑉∪𝐿)𝑐). Por tanto, la probabilidad de que juegue con videojuegos o lea libros es: 𝑃(𝑉∪𝐿)=1−𝑃(𝑉𝑐∩𝐿𝑐)=1−0,15=0,85.
  2. Sabemos que la probabilidad de jugar a videojuegos o leer libros viene dada por: 𝑃(𝑉∪𝐿)=𝑃(𝑉)+𝑃(𝐿)−𝑃(𝑉∩𝐿). Así que, despejando en la expresión anterior, la probabilidad de jugar a videojuegos y leer libros es: 𝑃(𝑉∩𝐿)=𝑃(𝑉)+𝑃(𝐿)−𝑃(𝑉∪𝐿)=0,65+0,45−0,85=0,25. Por tanto, la probabilidad de que juegue con videojuegos y no lea libros es: 𝑃(𝑉∩𝐿𝑐)=𝑃(𝑉)−𝑃(𝑉∩𝐿)=0,65−0,25=0,4.
  3. La probabilidad de que lea libros sabiendo que no juega con videojuegos es: 𝑃(𝐿|𝑉𝑐)=1−𝑃(𝐿𝑐|𝑉𝑐)=1−𝑃(𝐿𝑐∩𝑉𝑐)𝑃(𝑉𝑐)=1−𝑃(𝐿𝑐∩𝑉𝑐)1−𝑃(𝑉)=1−0,151−0,65≈0,5714.

Ejercicio 7

La resistencia media a la ruptura de una nueva gama de herramientas sigue una distribución Normal de desviación típica 15MPa (megapascales). Se seleccionan al azar 100 herramientas forjadas en la misma máquina durante el mismo proceso de producción, obteniéndose una resistencia media de 800MPa.

  1. Realizando la estimación con un nivel de confianza del 92%, ¿entre qué valores se estima la resistencia media poblacional de esta gama de herramientas?
  2. Manteniendo el mismo nivel de confianza, ¿cuál debe ser el tamaño mínimo de una nueva muestra para que el error máximo en la estimación de la resistencia media a la ruptura sea menor que 2MPa?

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Como el nivel de confianza es del 92%, entonces: 𝛼=1−0,92=0,08⇒1−𝛼2=1−0,082=0,96⇒𝑧𝛼/2=1,75. Por tanto, el intervalo de confianza para estimar la resistencia media de las herramientas con un nivel de confianza del 92% es: 𝐼=(800−1,75⋅15√100,800+1,75⋅15√100)=(797,375;802,625).
  2. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=1,75⋅15√𝑛=26,25√𝑛. Si se quiere que el error máximo sea menor que 2, entonces: 26,25√𝑛=2⇔√𝑛=26,252⇔𝑛=26,2524≈172,27. Por tanto, el tamaño mínimo de la muestra debe ser de 173 herramientas.

Ejercicio 8

Se quiere estudiar la proporción de perros que están vacunados en Andalucía. Para ello, se toma una muestra aleatoria de 400 perros de los que 320 resultan estar vacunados.

  1. Obtenga un intervalo con un nivel de confianza del 92% para estimar la proporción de perros vacunados en Andalucía y calcule el error máximo cometido.
  2. En una nueva muestra, manteniendo el mismo nivel de confianza y la misma proporción muestral, ¿cuántos perros, como mínimo, hay que elegir para que el error sea menor que 0,02?

Resolución
  1. Como 320 perros de 𝑛 =400 están vacunados, la proporción muestral es: 𝑝=320400=0,8. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 92%, entonces: 𝛼=1−0,92=0,08⇒1−𝛼2=1−0,082=0,96⇒𝑧𝛼/2=1,75. Por tanto, el intervalo de confianza para estimar la proporción poblacional de perros vacunados con un nivel de confianza del 92% es: 𝐼=(0,8−1,75⋅√0,8⋅(1−0,8)400,0,8+1,75⋅√0,8⋅(1−0,8)400)=(0,765;0,835). El error máximo cometido es: 𝐸=0,835−0,7652=0,035.
  2. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=1,75⋅√0,8⋅(1−0,8)𝑛=0,7√𝑛. Si se quiere que el error máximo sea de 0,02, entonces: 0,7√𝑛=0,02⇔√𝑛=0,70,02⇔𝑛=0,720,022=1.225. Por tanto, el tamaño mínimo de la muestra debe ser de 1.225 perros.