Icono Matemáticas de Selectividad

Buscar GitHub

📋 Julio de 2025

Ejercicio 1

  1. Un fabricante de paneles fotovoltaicos está analizando la eficiencia de tres modelos de placas (A, B y C). En un día determinado se realizaron tres pruebas. En la primera, utilizando 2 placas del modelo A, 1 placa del modelo B y 3 placas del modelo C, se generó una potencia efectiva total de 2.960 W. En la segunda, al combinar 1 placa del modelo A, 3 placas del modelo B y 2 placas del modelo C, se obtuvo una potencia efectiva total de 2.990 W. En la tercera, una configuración con 3 placas del modelo A, 2 placas del modelo B y 1 placa del modelo C produjo una potencia efectiva total de 2.870 W. Exprese el problema en forma matricial y discuta, a partir de la matriz del sistema, si se puede obtener la potencia efectiva que generó individualmente cada modelo de placa fotovoltaica. En caso afirmativo, obtenga dichas potencias efectivas.
  2. Resuelva la ecuación matricial 2𝑋=(110−1)2⋅(41).

Resolución

  1. Llamamos 𝑥, 𝑦 y 𝑧 a la potencia efectiva que generan los modelos A, B y C, respectivamente. Planteamos el sistema de ecuaciones. ⎧{ {⎨{ {⎩2𝑥+𝑦+3𝑧=2.960,𝑥+3𝑦+2𝑧=2.990,3𝑥+2𝑦+𝑧=2.870. De forma matricial, el sistema se puede escribir de la forma: ⎛⎜ ⎜ ⎜⎝213132321⎞⎟ ⎟ ⎟⎠⏟__⏟__⏟𝐴⎛⎜ ⎜ ⎜⎝𝑥𝑦𝑧⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝2.9602.9902.870⎞⎟ ⎟ ⎟⎠. Para discutir el sistema, estudiamos en primer lugar el rango de la matriz de coeficientes calculando su determinante. |𝐴|=∣213132321∣=−18≠0⇒rang⁡(𝐴)=3. Como el rango de la matriz de coeficientes es máximo, el sistema es compatible determinado. Por tanto, se puede obtener la potencia efectiva de cada modelo de placa.

    Resolvemos el sistema mediante el método de Gauss. ⎛⎜ ⎜ ⎜ ⎜⎝2132.9601322.9903212.870⎞⎟ ⎟ ⎟ ⎟⎠𝐹2−3𝐹1←←←←←←←←←→𝐹3−2𝐹1⎛⎜ ⎜ ⎜ ⎜⎝2132.960−50−7−5.890−10−5−3.050⎞⎟ ⎟ ⎟ ⎟⎠𝐹2−5𝐹1←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜⎝2132.96000189.360−10−5−3.050⎞⎟ ⎟ ⎟ ⎟⎠. El sistema escalonado resultante es: ⎧{ {⎨{ {⎩2𝑥+𝑦+3𝑧=2.960,18𝑧=9.360,−𝑥−5𝑧=−3.050⇔⎧{ {⎨{ {⎩2𝑥+𝑦+3𝑧=2.960,18𝑧=9.360,𝑥+5𝑧=3.050⇒⎧{ {⎨{ {⎩𝑥=450,𝑦=500,𝑧=520. Por tanto, las potencias efectivas de los modelos A, B y C son 450 W, 500 W y 520 W, respectivamente.

  2. Despejamos y resolvemos la ecuación matricial. 2𝑋=(110−1)2(41)⇔𝑋=12(110−1)2(41)=12(1001)(41)=(212).

Ejercicio 2

Un agricultor cultiva dos tipos de lechuga: iceberg y romana. Por razones de demanda, en cada ciclo de cultivo, la cantidad de iceberg debe ser al menos la mitad de la de romana, pero no puede superar las 1.500 unidades. Además, deben cultivarse en total entre 900 y 2.400 lechugas. El cultivo de iceberg requiere 15 litros de agua por unidad, mientras que el de romana necesita 18 litros de agua por unidad. ¿Cuántas unidades de cada tipo de lechuga deben cultivarse para minimizar el consumo total de agua?

Resolución

Llamamos 𝑥 al número de unidades de lechuga iceberg e 𝑦 al de lechuga romana.

Las restricciones del problema son: ⎧{ { { {⎨{ { { {⎩𝑥≥𝑦2,𝑥≤1.500,𝑥+𝑦≥900,𝑥+𝑦≤2.400,𝑥≥0,𝑦≥0⇔⎧{ { { {⎨{ { { {⎩2𝑥≥𝑦,𝑥≤1.500,𝑥+𝑦≥900,𝑥+𝑦≤2.400,𝑥≥0,𝑦≥0. La función objetivo a minimizar es: 𝐹(𝑥,𝑦)=15𝑥+18𝑦.

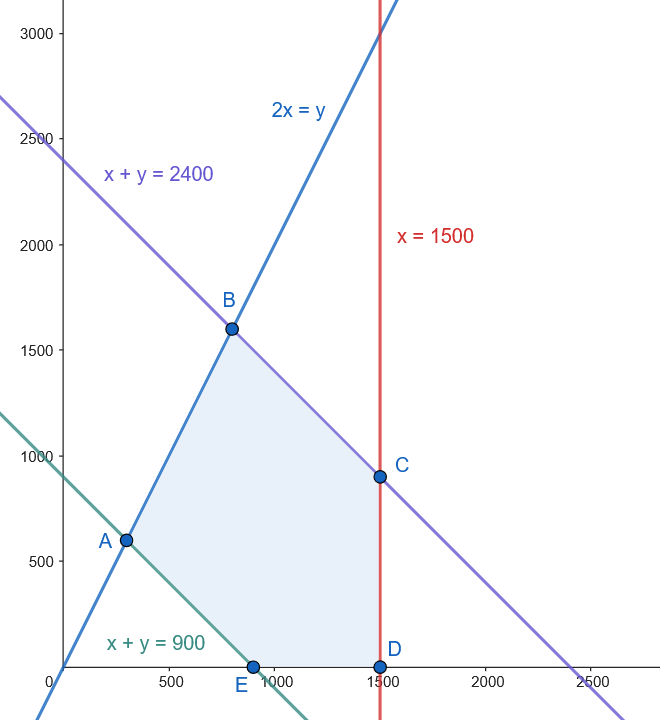Representamos la región. Figura Hallamos los vértices desconocidos.

  • Para determinar el vértice 𝐴, resolvemos el sistema: {2𝑥=𝑦,𝑥+𝑦=900⇔{𝑥=300,𝑦=600.
  • Para determinar el vértice 𝐵, resolvemos el sistema: {2𝑥=𝑦,𝑥+𝑦=2.400⇔{𝑥=800,𝑦=1.600.
  • Para determinar el vértice 𝐶, resolvemos el sistema: {𝑥=1.500,𝑥+𝑦=2.400⇔{𝑥=1.500,𝑦=900.
  • Para determinar el vértice 𝐸, resolvemos el sistema: {𝑥+𝑦=900,𝑦=0⇔{𝑥=900,𝑦=0.
Por tanto, los vértices son: 𝐴(300,600),𝐵(800,1.600),𝐶(1.500,900),𝐷(1.500,0)y𝐸(900,0).

Por el teorema fundamental de la programación lineal, el mínimo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(300,600)=15.300,𝐹(𝐵)=𝐹(800,1.600)=40.800,𝐹(𝐶)=𝐹(1.500,900)=38.700,𝐹(𝐷)=𝐹(1.500,0)=22.500,𝐹(𝐸)=𝐹(900,0)=13.500. Por tanto, el consumo de agua mínimo se alcanza cultivando 900 lechugas iceberg y ninguna lechuga romana.

Ejercicio 3

Trinidad, una persona ahorradora, deposita 5.000€ en un fondo de inversión y el capital final que obtiene cuando transcurren 𝑡 años viene dado por la siguiente función: 𝑓(𝑡)={5.000⋅(1+0,05𝑡),si 0≤𝑡≤1,5.000⋅1,05𝑡,si 𝑡>1.

  1. ¿Cuánto tiempo debe mantener invertido el dinero si el capital final que se obtiene es de 5.931,10€?
  2. Calcule los intereses que obtiene Trinidad entre el año 2 y el año 4, si se conoce que los intereses que genera esta inversión entre el año 𝑡1 y el año 𝑡2 vienen dados por 𝐼 =𝑓(𝑡2) −𝑓(𝑡1).
  3. Estudie la continuidad y derivabilidad de la función 𝑓.
  4. Estudie la monotonía de la función 𝑓 y esboce su gráfica.

Resolución
    • Si 0 ≤𝑡 ≤1, 𝑓(𝑡)=5.931,10⇔5.000⋅(1+0,05𝑡)=5.931,10⇔1+0,05𝑡=1,1862⇔0,05𝑡=0,1862⇔⇔𝑡=3,724∉[0,1].
    • Si 𝑡 >1, 𝑓(𝑡)=5.931,10⇔5.000⋅1,05𝑡=5.931,10⇔1,05𝑡=1,1862⇔𝑡=log1,05⁡(1,1862)≈3,5.
    Por tanto, debe mantener invertido el dinero alrededor de 3 años y medio.
  2. Calculamos los intereses. 𝐼=𝑓(4)−𝑓(2)=5.000⋅1,054−5.000⋅1,052≈565,0313€.
  3. Estudiamos la continuidad y la derivabilidad de 𝑓.
    • Si 𝑡 ∈[0, +∞) con 𝑡 ≠1, 𝑓 es continua y derivable con: 𝑓′(𝑡)={250,si 0<𝑡<1,5.000ln⁡(1,05)⋅1,05𝑡,si 𝑡>1.

    • Estudiamos la continuidad en 𝑡 =1. lím𝑡→1−⁡𝑓(𝑡)=lím𝑡→1−⁡5.000⋅(1+0,05𝑡)=5.250,lím𝑡→1+⁡𝑓(𝑡)=lím𝑡→1+⁡5.000⋅1,05𝑡=5.250,𝑓(1)=5.250. Observamos que: lím𝑡→1−⁡𝑓(𝑡)=lím𝑡→1+⁡𝑓(𝑡)=𝑓(1). Así que 𝑓 es continua en 𝑡 =1.

      Pasamos a estudiar la derivabilidad. 𝑓′−(1)=lím𝑡→1−⁡𝑓′(𝑡)=lím𝑡→1−⁡250=250,𝑓′+(1)=lím𝑡→1+⁡𝑓′(𝑡)=lím𝑡→1+⁡5.000⋅1,05𝑡⋅ln⁡(1,05)=5.250ln⁡(1,05)≈256,1484. Observamos que 𝑓′−(1) ≠𝑓′+(1), así que 𝑓 no es derivable en 𝑡 =1.

    Por tanto, 𝑓 es continua en [0, +∞] y derivable en [0,1) ∪(1, +∞).
  4. Para hallar los puntos críticos, igualamos las dos ramas de la derivada a cero.
    • Si 0 ≤𝑡 <1, 𝑓′(𝑡) =250 ≠0.
    • Si 𝑡 >1, 𝑓′(𝑡)=5.000⋅1,05𝑡⋅ln⁡(1,05)≠0.
    Así que la función no tiene ningún punto crítico. Consideramos 𝑡 =1 por ser no derivable. Estudiamos el signo de la derivada.
    (0,1) (1, +∞)
    signo de 𝑓′ + +
    monotonía de 𝑓 → →

    Por tanto, 𝑓 es creciente en todo su dominio.

    Representamos gráficamente la función.

    Figura

Ejercicio 4

En un determinado centro educativo, el 50% del alumnado aprueba Historia, el 70% aprueba Matemáticas y el 30% aprueba ambas asignaturas. Si se elige un alumno al azar:

  1. Halle la probabilidad de que apruebe solo una de las dos asignaturas.
  2. Halle la probabilidad de que no apruebe más de una asignatura.
  3. Halle la probabilidad de que apruebe Historia si ha suspendido Matemáticas.
  4. Determine si los sucesos "Aprobar Matemáticas" y "Aprobar Historia" son independientes. ¿Son incompatibles?

Resolución

Llamamos 𝐻 a aprobar Historia y 𝑀 a aprobar Matemáticas. Sabemos que: 𝑃(𝐻)=0,5,𝑃(𝑀)=0,7y𝑃(𝐻∩𝑀)=0,3.

  1. La probabilidad de que apruebe solo una de las dos asignaturas es: 𝑃(𝐻−𝑀)+𝑃(𝑀−𝐻)=𝑃(𝐻)−𝑃(𝐻∩𝑀)+𝑃(𝑀)−𝑃(𝐻∩𝑀)=0,5−0,3+0,7−0,3=0,6.
  2. La probabilidad de que no apruebe más de una asignatura es: 𝑃((𝐻∩𝑀)𝑐)=1−𝑃(𝐻∩𝑀)=1−0,3=0,7.
  3. La probabilidad de que apruebe Historia sabiendo que ha suspendido Matemáticas es: 𝑃(𝐻|𝑀𝑐)=𝑃(𝐻∩𝑀𝑐)𝑃(𝑀𝑐)=𝑃(𝐻)−𝑃(𝐻∩𝑀)1−𝑃(𝑀)=0,5−0,31−0,7=23.
  4. Como 𝑃(𝐻) ≠𝑃(𝐻|𝑀𝑐), los sucesos 𝐻 y 𝑀 no son independientes. Por otro lado, como 𝑃(𝐻 ∩𝑀) >0, los sucesos no son incompatibles.

Ejercicio 5

Los alumnos de un colegio de una localidad andaluza van a realizar una excursión a la estación de esquí de Sierra Nevada desplazándose en tres autobuses A, B y C. En el autobús A se desplazan cuatro novenos de los alumnos de la excursión, en el B se desplaza la tercera parte y el resto van en el autobús C. Se sabe que el 65% de los alumnos que viajan en el autobús A y el 40% de los del autobús B no sabe esquiar y todos los del autobús C sí que saben esquiar. Se escoge al azar a uno de los alumnos de la excursión. Calcule la probabilidad de que:

  1. Sepa esquiar.
  2. Viaje en el autobús C, si sabe esquiar.
  3. Sepa esquiar y no viaje en el autobús B.

Resolución

Llamamos 𝐴, 𝐵 y 𝐶 a viajar en los autobuses A, B y C, respectivamente, y 𝐸 a saber esquiar. Podemos organizar los datos en un diagrama de árbol.

𝐸
0,35←←←←←←←←←←←→
𝐴
4/9←←←←←←←←←←←→ 0,65←←←←←←←←←←←→
𝐸𝑐
𝐸
0,6←←←←←←←←←←→
1/3←←←←←←←←←←←→ 𝐵
0,4←←←←←←←←←←→
𝐸𝑐
2/9←←←←←←←←←←←→
𝐶 1←←←←←←←←←→ 𝐸
  1. Por el teorema de la probabilidad total, la probabilidad de que un alumno sepa esquiar es: 𝑃(𝐸)=𝑃(𝐸∩𝐴)+𝑃(𝐸∩𝐵)+𝑃(𝐸∩𝐶)=𝑃(𝐴)⋅𝑃(𝐸|𝐴)+𝑃(𝐵)⋅𝑃(𝐸|𝐵)+𝑃(𝐶)==49⋅0,35+13⋅0,6+29≈0,5778.
  2. La probabilidad de que un alumno viaje en el autobús C sabiendo que es capaz de esquiar es: 𝑃(𝐶|𝐸)=𝑃(𝐶∩𝐸)𝑃(𝐸)=𝑃(𝐶)𝑃(𝐸)=290,5778≈0,3846.
  3. La probabilidad de que un alumno sepa esquiar y no viaje en el autobús B es: 𝑃(𝐸∩𝐵𝑐)=𝑃(𝐸)−𝑃(𝐸∩𝐵)=𝑃(𝐸)−𝑃(𝐵)⋅𝑃(𝐸|𝐵)=0,5778−13⋅0,6=0,3778.

Ejercicio 6

A partir de un estudio muestral se sabe que, con un nivel de confianza del 95%, la proporción de estudiantes de una universidad que tienen carnet de conducir pertenece al intervalo (0,5616; 0,7184).

  1. Calcule la proporción muestral de estudiantes que tienen carnet de conducir.
  2. Calcule el error máximo cometido en la estimación de la proporción poblacional.
  3. Calcule el tamaño de la muestra seleccionada.
  4. Razone qué efecto producirá sobre la amplitud del intervalo un aumento del tamaño muestral.

Resolución
  1. La proporción muestral viene dada por el punto medio del intervalo. 𝑝=0,5616+0,71842=0,64.
  2. El error cometido viene dado por la mitad de la amplitud del intervalo. 𝐸=0,7184−0,56162=0,0784.
  3. Como el nivel de confianza es del 95%, entonces: 𝛼=1−0,95=0,05⇒1−𝛼2=1−0,052=0,975⇒𝑧𝛼/2=1,96. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛. Despejando en la ecuación, podemos calcular el tamaño de la muestra como: 𝑛=𝑧2𝛼/2⋅𝑝⋅(1−𝑝)𝐸2=1,962⋅0,64⋅(1−0,64)0,07842=144.
  4. La amplitud del intervalo disminuye al aumentar el tamaño de la muestra, porque el error máximo cometido se reduce.

Ejercicio 7

El tiempo de adaptación a la guardería, en días, de los menores de dos años andaluces, sigue una distribución Normal de media 10,5 días y desviación típica 1,5 días.

  1. Se toma una muestra aleatoria de 25 menores de estas características. ¿Qué distribución sigue la media muestral del tiempo de adaptación? ¿Cuál es la probabilidad de que el tiempo medio de adaptación de esta muestra supere los 10 días?
  2. ¿Qué porcentaje de muestras de tamaño 25 nos proporcionará un tiempo medio de adaptación entre 8 y 11 días?

Resolución
  1. La distribución de la media muestral ――𝑋 sigue una normal 𝑁(𝜇,𝜎√𝑛) con 𝜇 =10,5, 𝜎 =1,5 y 𝑛 =25. Es decir, ――𝑋∼𝑁(10,5;1,5√25)=𝑁(10,5;0,3). La probabilidad de que el tiempo medio de adaptación de esta muestra supere los 10 días es: 𝑃(――𝑋>10)=𝑃(𝑍>10−10,50,3)=𝑃(𝑍>−1,67)=𝑃(𝑍<1,67)=0,9525.
  2. La probabilidad de que el tiempo medio de adaptación esté entre 8 y 11 días es: 𝑃(8<――𝑋<11)=𝑃(8−10,50,3<𝑍<11−10,50,3)=𝑃(−8,33<𝑍<1,67)==𝑃(𝑍<1,67)−𝑃(𝑍<−8,33)=0,9525. Por tanto, el porcentaje de muestras de tamaño 25 que presenta un tiempo medio de adaptación entre 8 y 11 días es el 95,25%.