Icono Matemáticas de Selectividad

Buscar GitHub

📋 Junio de 2021

Ejercicio 1

Una empresa de recambios industriales produce dos tipos de baterías, A y B. Su producción semanal debe ser de al menos 10 baterías en total y el número de baterías de tipo B no puede superar en más de 10 unidades a las fabricadas de tipo A. Cada batería de tipo A tiene unos gastos de producción de 150 euros y cada batería de tipo B de 100 euros, disponiendo de un máximo de 6.000 euros a la semana para el coste total de producción. Si la empresa vende todo lo que produce y cada batería de tipo A genera un beneficio de 130 euros y la de tipo B de 140 euros, ¿cuántas baterías de cada tipo tendrán que producir a la semana para que el beneficio total sea máximo? ¿Cuál es ese beneficio?

Resolución

Llamamos 𝑥 al número de baterías de tipo A e 𝑦 al de tipo B.

Las restricciones del problema son: ⎧{ { { {⎨{ { { {⎩𝑥+𝑦≥10,𝑦≤𝑥+10,150𝑥+100𝑦≤6.000,𝑥≥0,𝑦≥0⇔⎧{ { { {⎨{ { { {⎩𝑥+𝑦≥10,𝑦≤𝑥+10,3𝑥+2𝑦≤120,𝑥≥0,𝑦≥0. La función objetivo a maximizar es: 𝐹(𝑥,𝑦)=130𝑥+140𝑦.

Representamos la región factible. 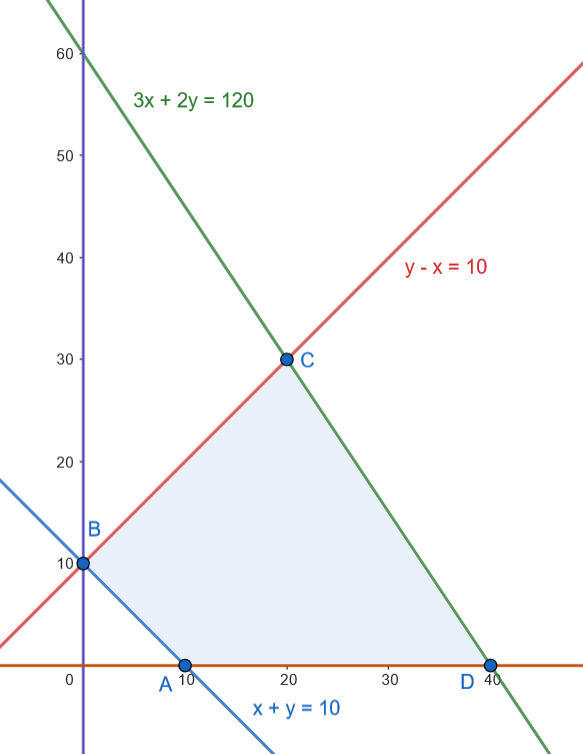Figura Los vértices son: 𝐴(10,0),𝐵(0,10),𝐶(20,30)y𝐷(40,0).

Por el teorema fundamental de la programación lineal, el máximo de la función se alcanza en uno de los vértices de la región en caso de existir. Evaluamos la función en los vértices. 𝐹(𝐴)=𝐹(10,0)=1.300,𝐹(𝐵)=𝐹(0,10)=1.400,𝐹(𝐶)=𝐹(20,30)=6.800,𝐹(𝐷)=𝐹(40,0)=5.200. Por tanto, el beneficio máximo se alcanza produciendo semanalmente 20 baterías de tipo A y 30 de tipo B, con unas ganancias de 6.800€.

Ejercicio 2

Se considera la matriz 𝐴=⎛⎜ ⎜ ⎜⎝1−1𝑚02−3𝑚11⎞⎟ ⎟ ⎟⎠, con 𝑚 un parámetro real.

  1. ¿Para qué valores del parámetro 𝑚 existe la matriz inversa de 𝐴?
  2. Para 𝑚 =2, resuelva la ecuación matricial 𝑋𝐴 −𝐴2 =𝐼3.

Resolución
  1. Calculamos en primer lugar el determinante de la matriz 𝐴. |𝐴|=∣1−1𝑚02−3𝑚11∣=2+3𝑚−2𝑚2+3=−2𝑚2+3𝑚+5. La matriz inversa de 𝐴 existe si y solo si su determinante es no nulo. |𝐴|=0⇔−2𝑚2+3𝑚+5=0⇔{𝑚=−1,𝑚=52. Por tanto, la matriz 𝐴 tiene inversa si 𝑚 ≠ −1 y 𝑚 ≠52.
  2. Si 𝑚 =2, por el apartado anterior 𝐴 es invertible con det(𝐴) =3. Despejamos la ecuación matricial. 𝑋𝐴−𝐴2=𝐼3⇔𝑋𝐴=𝐼3+𝐴2⇔𝑋=(𝐼3+𝐴2)𝐴−1=𝐴−1+𝐴. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝5−6−43−3−3−132⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=13⎛⎜ ⎜ ⎜⎝53−1−6−33−4−32⎞⎟ ⎟ ⎟⎠. Por tanto, 𝑋=𝐴−1+𝐴=13⎛⎜ ⎜ ⎜⎝53−1−6−33−4−32⎞⎟ ⎟ ⎟⎠+⎛⎜ ⎜ ⎜⎝1−1202−3211⎞⎟ ⎟ ⎟⎠==13⎛⎜ ⎜ ⎜⎝53−1−6−33−4−32⎞⎟ ⎟ ⎟⎠+13⎛⎜ ⎜ ⎜⎝3−3606−9633⎞⎟ ⎟ ⎟⎠=13⎛⎜ ⎜ ⎜⎝805−63−6205⎞⎟ ⎟ ⎟⎠.

Ejercicio 3

Se considera la función 𝑓(𝑥) =𝑥3 −4𝑥2 +4𝑥.

  1. Estudie su monotonía y calcule sus extremos.
  2. Represente gráficamente la función.
  3. Calcule ∫𝑓(𝑥)𝑑𝑥.
  4. Calcule el área del recinto acotado limitado por la gráfica de 𝑓 y el eje de abscisas.

Resolución
  1. En primer lugar, hallamos la derivada de la función 𝑓. 𝑓′(𝑥)=3𝑥2−8𝑥+4. Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔3𝑥2−8𝑥+4=0⇔{𝑥=23,𝑥=2. Estudiamos el signo de $la derivada.
    (−∞,23) (23,2) (2, +∞)
    signo de 𝑓′ + − +
    monotonía de 𝑓 → → →
    Por tanto, 𝑓 es creciente en (−∞,23) ∪(2, +∞) y decreciente en (23,2). Además, el punto (23,3227) es un máximo relativo y (2,0) es un mínimo relativo.
  2. Representamos gráficamente la función usando la información del apartado anterior. Figura
  3. Calculamos la integral indefinida. ∫𝑓(𝑥)𝑑𝑥=∫(𝑥3−4𝑥2+4𝑥)𝑑𝑥=14𝑥4−43𝑥2+2𝑥2+𝐶.
  4. Podemos representar el recinto acotado limitado por la gráfica de 𝑓 y el eje 𝑋. Figura Calculamos el área. ∫20(𝑥3−4𝑥2+4𝑥)𝑑𝑥=[14𝑥4−43𝑥2+2𝑥2]20=4−323+8=43𝑢2.

Ejercicio 4

  1. Calcule la derivada de las siguientes funciones: 𝑓(𝑥)=ln⁡(𝑥−1𝑥+1),𝑔(𝑥)=𝑥3𝑒2𝑥2.
  2. Represente gráficamente la parábola ℎ(𝑥) =𝑥2 +𝑥 +1, indicando el vértice y los puntos de corte con los ejes coordenados.
  3. Calcule el área del recinto limitado por la gráfica de ℎ(𝑥) =𝑥2 +𝑥 +1, el eje de abscisas y las rectas 𝑥 = −12 y 𝑥 =0.

Resolución
    • En primer lugar, observamos que 𝑓(𝑥)=ln⁡(𝑥−1𝑥+1)=ln⁡(𝑥−1)−ln⁡(𝑥+1). Calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=1𝑥−1+1𝑥+1=2𝑥2−1.
    • Calculamos la derivada de la función 𝑔. 𝑔′(𝑥)=3𝑥2⋅𝑒2𝑥2+𝑥3⋅𝑒2𝑥2⋅4𝑥=𝑥2𝑒𝑥2(4𝑥2+3).
    • La parábola tiene vértice (−12,34).
    • Hallamos los puntos de corte con el eje 𝑋, es decir, aquellos puntos con coordenada 𝑦 =0. Observamos que ℎ(𝑥)=𝑥2+𝑥+1≠0, así que la función no corta al eje 𝑋.
    • Hallamos el punto de corte con el eje 𝑌. Observamos que ℎ(0) =1, así que el punto de corte es (0,1).
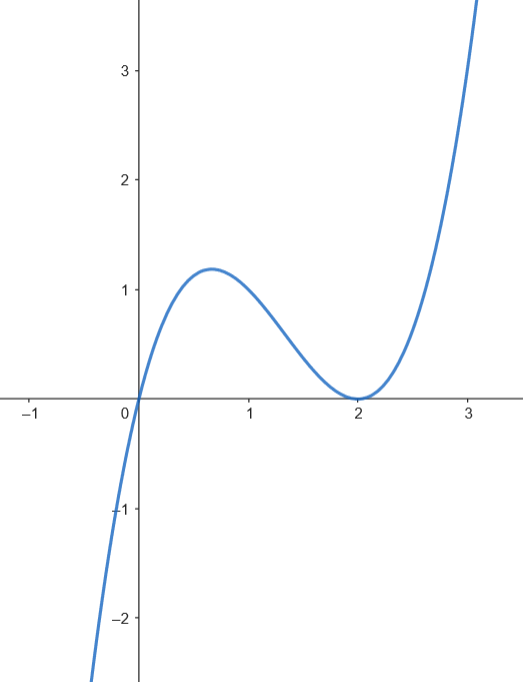
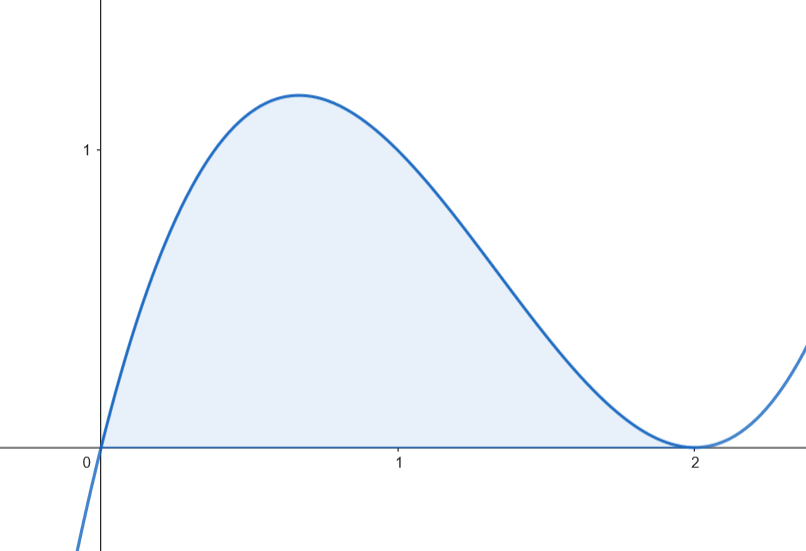    Representamos gráficamente la función. Figura
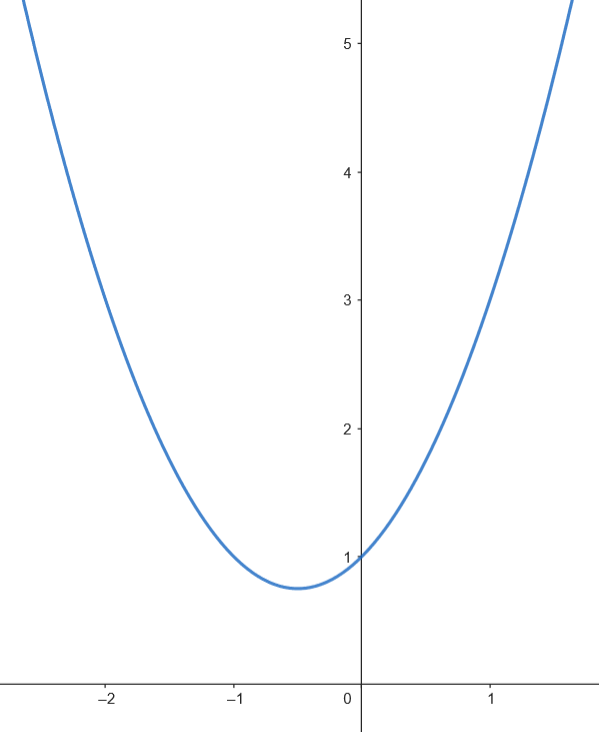
  3. Podemos representar el recinto acotado limitado por la gráfica de ℎ, el eje 𝑋 y las rectas 𝑥 = −12 y 𝑥 =0. Figura Calculamos el área. ∫0−12ℎ(𝑥)𝑑𝑥=∫0−12(𝑥2+𝑥+1)𝑑𝑥=[13𝑥3+12𝑥2+𝑥]0−12=−(−124+18−12)=512𝑢2.

Ejercicio 5

Se desea probar la eficacia de dos tipos de vacunas, A y B, contra un virus determinado. Para ello, se seleccionan 5.000 voluntarios sin anticuerpos para este virus, a los que se les administra una de las vacunas o un placebo, resultando que 3.000 reciben la vacuna A, 1.500 la B y el resto el placebo. Se comprueba que el 90% de los vacunados con la A y el 95% de los vacunados con la B, generan anticuerpos, no generando anticuerpos los que han recibido el placebo. Se selecciona uno de esos voluntarios al azar.

  1. ¿Cuál es la probabilidad de que haya generado anticuerpos?
  2. Si dicho voluntario no ha generado anticuerpos, ¿qué probabilidad hay de que se le haya administrado placebo?

Resolución

Llamamos 𝐴 a administrar la vacuna A, 𝐵 a administrar la vacuna B, 𝐶 a administrar el placebo y 𝐷 a generar anticuerpos. Sabemos que: 𝑃(𝐴)=3.0005.000=0,6y𝑃(𝐵)=1.5005.000=0,3. Podemos hacer un diagrama de árbol.

𝐷
0,9←←←←←←←←←←→
𝐴
0,6←←←←←←←←←←→ 0,1←←←←←←←←←←→
𝐷𝑐
𝐷
0,95←←←←←←←←←←←→
0,3←←←←←←←←←←→ 𝐵
0,05←←←←←←←←←←←→
𝐷𝑐
0,1←←←←←←←←←←→
𝐶 1←←←←←←←←←→ 𝐷𝑐
  1. Por el teorema de la probabilidad total, la probabilidad de que haya generado anticuerpos es: 𝑃(𝐷)=𝑃(𝐴)⋅𝑃(𝐷|𝐴)+𝑃(𝐵)⋅𝑃(𝐷|𝐵)=0,6⋅0,9+0,3⋅0,95=0,825.
  2. La probabilidad de que se le haya administrado placebo sabiendo que no ha generado anticuerpos es: 𝑃(𝐶|𝐷𝑐)=𝑃(𝐶∩𝐷𝑐)𝑃(𝐷𝑐)=𝑃(𝐶)1−𝑃(𝐷)=0,11−0,825≈0,5714.

Ejercicio 6

De las compras realizadas en el último período de rebajas del pasado año, el 55% se dedicaron a productos electrónicos, el 72% se hicieron a través de Internet y, de las compras que se hicieron por Internet, el 64% fueron de productos electrónicos. Se elige una compra al azar.

  1. Calcule la probabilidad de que haya sido de productos electrónicos y se haya realizado por Internet.
  2. Calcule la probabilidad de que la compra se haya realizado por Internet o que se hayan comprado productos electrónicos.
  3. Calcule la probabilidad de que sabiendo que no se compraron productos electrónicos, la compra no se hiciera a través de Internet.

Resolución

Llamamos 𝐸 a comprar productos electrónicos e 𝐼 a comprar productos por Internet. Sabemos que 𝑃(𝐸)=0,55,𝑃(𝐼)=0,72y𝑃(𝐸|𝐼)=0,64.

  1. La probabilidad de que la compra haya sido de productos electrónicos y se haya realizado por Internet es 𝑃(𝐸∩𝐼)=𝑃(𝐼)⋅𝑃(𝐸|𝐼)=0,72⋅0,64=0,4608.
  2. La probabilidad de que la compra se haya realizado por Internet o que se hayan comprado productos electrónicos es 𝑃(𝐸∪𝐼)=𝑃(𝐸)+𝑃(𝐼)−𝑃(𝐸∩𝐼)=0,55+0,72−0,4608=0,8092.
  3. La probabilidad de que la compra no se haya realizado por Internet sabiendo que no se han comprado productos electrónicos es 𝑃(𝐼𝑐|𝐸𝑐)=𝑃(𝐼𝑐∩𝐸𝑐)𝑃(𝐸𝑐)=𝑃((𝐼∪𝐸)𝑐)1−𝑃(𝐸)=1−𝑃(𝐼∪𝐸)1−𝑃(𝐸)=1−0,80921−0,55=0,424.

Ejercicio 7

  1. En una Escuela Politécnica hay matriculados en el último curso 60 estudiantes de Ingeniería Eléctrica, 40 de Ingeniería Informática, 30 de Ingeniería Civil, 50 de Ingeniería Mecánica y 20 de Ingeniería Aeronáutica. Se quiere hacer una encuesta al 20% de estos estudiantes, de manera proporcional al número de matriculados en cada titulación.
    1. ¿Qué tipo de muestreo se debe emplear?
    2. ¿Cuántos alumnos debe haber en la muestra y cuántos de cada titulación?
  2. Dada la población {𝑎,10,12,11,18}, ¿cuánto debe valer 𝑎, sabiendo que la media de las medias muestrales de tamaño 3, obtenidas mediante muestreo aleatorio simple, es 13,2?

Resolución
    1. Se debe emplear un muestreo aleatorio estratificado con afijación proporcional.
    2. El tamaño de la población es 60+40+30+50+20=200. Como se quiere tomar una muestra compuesta por el 20% de la población, debe estar formada por 200 ⋅0,2 =40 estudiantes.
      • De Ingeniería Eléctrica se deben tomar 60 ⋅0,2 =12 estudiantes.
      • De Ingeniería Informática se deben tomar 40 ⋅0,2 =8 estudiantes.
      • De Ingeniería Civil se deben tomar 30 ⋅0,2 =6 estudiantes.
      • De Ingeniería Mecánica se deben tomar 50 ⋅0,2 =10 estudiantes.
      • De Ingeniería Aeronáutica se deben tomar 20 ⋅0,2 =4 estudiantes.
  2. La media 𝜇 de la población viene dada por 𝜇=𝑎+10+12+11+185=51+𝑎5. Como la media de las medias muestrales coincide con la media poblacional 𝜇, entonces 𝜇=13,2⇔51+𝑎5=13,2⇔51+𝑎=66⇔𝑎=15.

Ejercicio 8

Se desea estimar la proporción de individuos mayores de edad de una localidad que están en contra de la construcción de una central nuclear en su término municipal. Para ello, se pregunta a 100 individuos mayores de edad de esa localidad, elegidos de forma aleatoria, resultando que 45 de ellos rechazan la construcción de la central.

  1. Calcule un intervalo de confianza al 92% para estimar la proporción real de individuos de esa localidad que están en contra de la construcción de la central.
  2. Suponiendo que se mantiene la misma proporción muestral y el mismo nivel de confianza del apartado anterior, determine el tamaño mínimo de la muestra que hay que tomar, para que al estimar la proporción de individuos de esa localidad que rechazan la construcción de la central, el error cometido sea inferior al 5%.

Resolución
  1. Como 45 personas de 𝑛 =100 están en contra de la construcción de una central nuclear, la proporción muestral es: 𝑝=45100=0,45. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 92%, entonces: 𝛼=1−0,92=0,08⇒1−𝛼2=1−0,082=0,96⇒𝑧𝛼/2=1,75. Por tanto, el intervalo de confianza para estimar la proporción poblacional de personas que están en contra de la construcción de una central nuclear con un nivel de confianza del 92% es: 𝐼=(0,45−1,75⋅√0,45⋅(1−0,45)100,0,45+1,75⋅√0,45⋅(1−0,45)100)≈(0,3629;0,5371).
  2. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=1,75⋅√0,45⋅(1−0,45)𝑛=1,75⋅√0,2475√𝑛. Si se quiere que el error cometido sea inferior a 0,05, entonces: 1,75⋅√0,2475√𝑛=0,05⇔√𝑛=1,75⋅√0,24750,05⇔𝑛=1,752⋅0,24750,052=303,1875. Por tanto, el tamaño mínimo de la muestra debe ser de 304 personas.