Icono Matemáticas de Selectividad

Buscar GitHub

📋 Julio de 2022

Ejercicio 1

Se consideran las matrices 𝐴=⎛⎜ ⎜ ⎜⎝112−2010−1−1⎞⎟ ⎟ ⎟⎠,𝐵=⎛⎜ ⎜ ⎜⎝−213102⎞⎟ ⎟ ⎟⎠y𝐶=⎛⎜ ⎜ ⎜⎝12−1−1−23⎞⎟ ⎟ ⎟⎠.

  1. Determine la matriz 𝑋 que verifica 𝐴𝑋 +𝐵 =𝐴2𝐶.
  2. Determine las dimensiones de dos matrices 𝑃 y 𝑄 sabiendo que 𝐴𝑃𝑡+𝐶=𝐶(𝑄𝐵).

Resolución
  1. Comprobamos en primer lugar que la matriz 𝐴 es invertible. |𝐴|=∣112−2010−1−1∣=4−2+1=3≠0. Por tanto, 𝐴 es invertible. Resolvemos la ecuación matricial. 𝐴𝑋+𝐵=𝐴2𝐶⇔𝐴𝑋=𝐴2𝐶−𝐵⇔𝑋=𝐴−1(𝐴2𝐶−𝐵)=𝐴𝐶−𝐴−1𝐵. Para hallar la inversa de 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝1−22−1−111−52⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=13⎛⎜ ⎜ ⎜⎝1−11−2−1−5212⎞⎟ ⎟ ⎟⎠. Por último, calculamos la matriz 𝑋 operando. 𝑋=𝐴𝐶−𝐴−1𝐵=⎛⎜ ⎜ ⎜⎝112−2010−1−1⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝12−1−1−23⎞⎟ ⎟ ⎟⎠−13⎛⎜ ⎜ ⎜⎝1−11−2−1−5212⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝−213102⎞⎟ ⎟ ⎟⎠==⎛⎜ ⎜ ⎜⎝−47−4−13−2⎞⎟ ⎟ ⎟⎠−13⎛⎜ ⎜ ⎜⎝−521−13−17⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜ ⎜⎝−73193−133103103−133⎞⎟ ⎟ ⎟ ⎟ ⎟⎠.
    • 𝐶 es de dimensión 3 ×2, así que 𝐴𝑃𝑡 debe tener la misma dimensión para poder sumarse con ella. Como 𝐴 es 3 ×3, 𝑃𝑡 debe tener 3 filas para poder multiplicarse y 2 columnas para dar como resultado una matriz de dimensión 3 ×2. Por tanto, 𝑃 es de dimensión 2 ×3.
    • 𝐵 y 𝐶 son de dimensión 3 ×2, así que 𝑄 debe tener 2 filas y 3 columnas para poder multiplicarse con ellas. Por tanto, 𝑄 es de dimensión 2 ×3. Observamos que entonces el producto 𝐶(𝑄𝐵) es de dimensión 3 ×2, por lo que coincide con el otro lado de la igualdad.

Ejercicio 2

Se considera el recinto limitado por las siguientes inecuaciones: 𝑦−2𝑥≤7,−𝑥+3𝑦≤21,𝑥+2𝑦≤19,𝑥+𝑦≤14.

  1. Represente dicho recinto y determine sus vértices.
  2. Calcule los valores máximo y mínimo de la función 𝐹(𝑥,𝑦) =𝑥 +4𝑦 en el recinto anterior, así como los puntos donde se alcanzan.
  3. ¿Podría tomar la función objetivo 𝐹 el valor 40 en algún punto de la región factible? ¿Y el valor 20? Justifique las respuestas.

Resolución
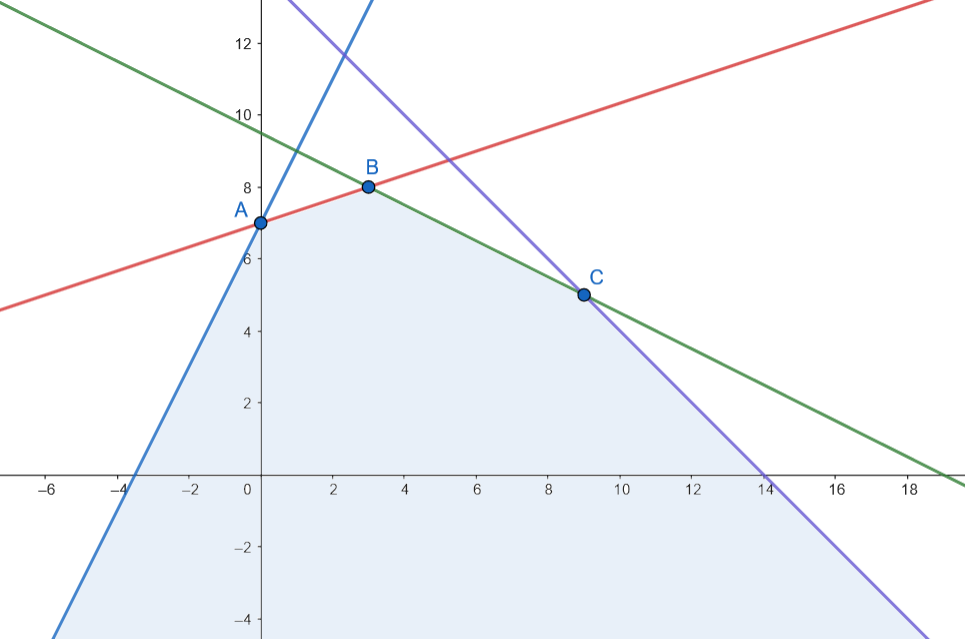  1. Dibujamos la región. Figura Los vértices son 𝐴(0,7),𝐵(3,8)y𝐶(9,5).
  2. El recinto no está acotado inferiormente, así que la función objetivo no tiene mínimo. Para hallar el valor máximo de 𝐹, la evaluamos en los vértices. 𝐹(𝐴)=𝐹(0,7)=28,𝐹(𝐵)=𝐹(3,8)=35y𝐹(𝐶)=𝐹(9,5)=29. Por tanto, el máximo es 35 y se alcanza en el punto 𝐵(3,8).
  3. Como el valor máximo de la función objetivo en la región factible es 35, ningún punto de la región puede alcanzar el valor 40. En cambio, el valor 20 sí puede tomarse puesto que la función no tiene mínimo en la región.

Ejercicio 3

  1. Se considera la función 𝑓(𝑥) =𝑥3 +𝑏𝑥2 +𝑐𝑥 −1 donde 𝑏 y 𝑐 son números reales. Determine el valor de 𝑏 y 𝑐 para que la función 𝑓 presente un extremo en el punto de abscisa 𝑥 =13 y además la gráfica de la función 𝑓 pase por el punto ( −2, −3).
  2. Dada la función 𝑔(𝑥) = −𝑥3 −𝑥2 +𝑥 +1, realice el esbozo de su gráfica, estudiando los puntos de corte con los ejes coordenados y su monotonía. Determine el área del recinto acotado, limitado por la gráfica de la función 𝑔 y el eje de abscisas.

Resolución
  1. En primer lugar, hallamos la derivada de la función 𝑓. 𝑓′(𝑥)=3𝑥2+2𝑏𝑥+𝑐.
    • Si la función tiene un extremo en 𝑥 =13, entonces 𝑓′(13) =0. 𝑓′(13)=0⇔13+23𝑏+𝑐=0⇔1+2𝑏+3𝑐=0⇔2𝑏+3𝑐=−1.
    • Si la función pasa por el punto ( −2, −3), entonces 𝑓( −2) = −3. 𝑓(−2)=−3⇔−8+4𝑏−2𝑐−1=−3⇔4𝑏−2𝑐=6⇔2𝑏−𝑐=3.
    Planteamos el sistema de ecuaciones {2𝑏+3𝑐=−1,2𝑏−𝑐=3. Resolvemos el sistema por reducción. Si restamos las dos ecuaciones, obtenemos que 4𝑐=−4⇔𝑐=−1. Despejando y sustituyendo en la segunda ecuación, 2𝑏−𝑐=3⇔𝑏=3+𝑐2𝑐=−1←←←←←←←→𝑏=1.
    • Hallamos los puntos de corte de la función 𝑔 con el eje 𝑋, es decir, aquellos puntos con 𝑦 =0. 𝑔(𝑥)=0⇔−𝑥3−𝑥2+𝑥+1=0⇔−(𝑥−1)(𝑥+1)2=0⇔{𝑥=−1,𝑥=1. Luego los puntos de corte con el eje 𝑋 son ( −1,0) y (1,0).
    • Hallamos el punto de corte con el eje 𝑌, es decir, aquel con 𝑥 =0. 𝑔(0)=1. Luego el punto de corte con el eje 𝑌 es (0,1).
    • Estudiamos la monotonía. En primer lugar, calculamos la derivada de la función 𝑔. 𝑔′(𝑥)=−3𝑥2−2𝑥+1. Para hallar los puntos críticos, igualamos la derivada de la función 𝑔. 𝑔′(𝑥)=0⇔−3𝑥2−2𝑥+1=0⇔{𝑥=−1,𝑥=13. Estudiemos el signo de la derivada.
      ( −∞, −1) (−1,13) (13,+∞)
      signo de 𝑔′ − + −
      monotonía de 𝑔 → → →
      Por tanto, 𝑓 es creciente en (−1,13) y decreciente en ( −∞, −1) ∪(13,+∞). Además, el punto (13,3227) es un máximo relativo y el punto ( −1,0) es un mínimo relativo.
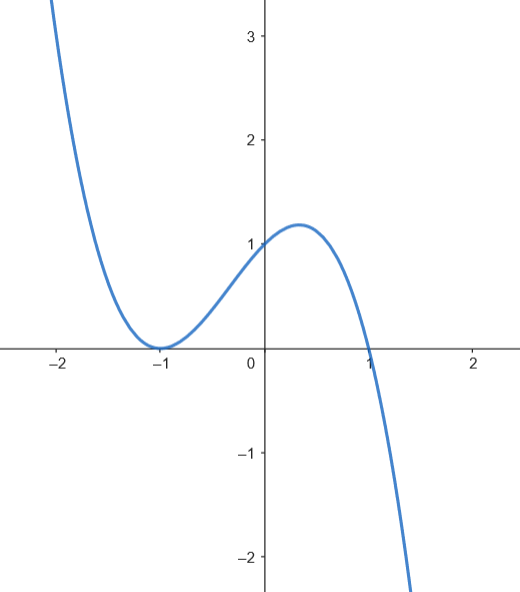    Representamos gráficamente la función usando esta información. Figura Podemos representar gráficamente el recinto acotado limitado por la gráfica de 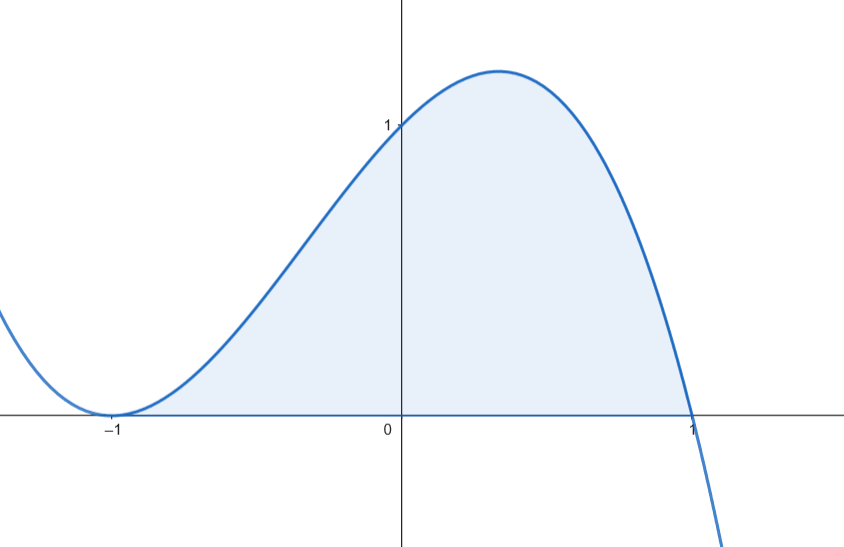𝑔 y el eje 𝑋. Figura Calculamos el área. ∫1−1𝑔(𝑥)𝑑𝑥=∫1−1(−𝑥3−𝑥2+𝑥+1)𝑑𝑥=[−14𝑥4−13𝑥3+12𝑥2+𝑥]1−1==−14−13+12+1−(−14+13+12−1)=43𝑢2.

Ejercicio 4

El beneficio, en miles de euros, que se obtiene en una pequeña finca familiar por la venta de aceitunas, en miles de kilogramos, viene dado por la siguiente función: 𝐵(𝑥)=−0,02𝑥2+1,3𝑥−15,𝑥≥0.

  1. Represente la función beneficio y calcule los puntos de corte con el eje 𝑂𝑋.
  2. ¿Para qué valores de 𝑥 la finca no tiene pérdidas?
  3. ¿Para qué número de kilogramos el beneficio será máximo? ¿Cuánto vale dicho beneficio?
  4. ¿Cuántos kilogramos debe vender para obtener un beneficio de 5.000€?

Resolución
  1. En primer lugar, hallamos los puntos de corte de la función 𝐵 con el eje 𝑋. 𝐵(𝑥)=0⇔−0,02𝑥2+1,3𝑥−15=0⇔𝑥2−65𝑥+750=0⇔{𝑥=15,𝑥=50. Luego los puntos de corte con el eje 𝑋 son (15,0) y (50,0). Además, observamos que 𝑓 es una parábola con vértice (652,498) =(32,5; 6,125). Representamos la función con esta información. Figura
  2. La finca no tiene pérdidas cuando 𝐵(𝑥) ≥0, es decir, si 15 ≤𝑥 ≤50.
  3. La función 𝐵 alcanza el máximo en el vértice (32,5; 6,125). Por tanto, el beneficio será máximo para 32.500 kg y ascenderá a 6.125€.
  4. Se obtiene un beneficio de 5.000€ si 𝐵(𝑥) =5. 𝐵(𝑥)=5⇔−0,02𝑥2+1,3𝑥−15=5⇔−0,02𝑥2+1,3𝑥−20=0⇔{𝑥=25,𝑥=40. Por tanto, se deben vender 25.000 kg o 40.000 kg para obtener dicho beneficio.

Ejercicio 5

En una determinada región hay tres universidades A, B y C. De los estudiantes que terminaron sus estudios el año pasado, el 60% procedían de la universidad A, el 30% de la universidad B y el resto de C. Además, se conoce que la probabilidad de que un estudiante de la universidad A no encuentre trabajo en su región es 0,4 y para un estudiante de B es 0,5.

  1. Si la probabilidad de que un estudiante no encuentre trabajo en su región es 0,395, determine la probabilidad de que un estudiante de la universidad C encuentre trabajo en su región.
  2. Calcule la probabilidad de que un estudiante que no haya encontrado trabajo en su región proceda de la universidad A o de la B.

Resolución

Llamamos 𝐴 a proceder de la universidad A, 𝐵 de la universidad B, 𝐶 de la universidad C y 𝑇 a encontrar trabajo en la región. Podemos hacer un diagrama de árbol.

𝑇
0,6←←←←←←←←←←→
𝐴
0,6←←←←←←←←←←→ 0,4←←←←←←←←←←→
𝑇𝑐
𝑇
0,5←←←←←←←←←←→
0,3←←←←←←←←←←→ 𝐵
0,5←←←←←←←←←←→
𝑇𝑐
𝑇
0,1←←←←←←←←←←→ 1−𝑝←←←←←←←←←←←→
𝐶
𝑝←←←←←←←←←→
𝑇𝑐
  1. Sabemos que 𝑃(𝑇𝑐) =0,395. Por el teorema de la probabilidad total, la probabilidad de que un estudiante no encuentre trabajo en su región viene dada por: 𝑃(𝑇𝑐)=𝑃(𝑇𝑐∩𝐴)+𝑃(𝑇𝑐∩𝐵)+𝑃(𝑇𝑐∩𝐶)=𝑃(𝐴)⋅𝑃(𝑇𝑐|𝐴)+𝑃(𝐵)⋅𝑃(𝑇𝑐|𝐵)+𝑃(𝐶)⋅𝑃(𝑇𝑐|𝐶)==0,6⋅0,4+0,3⋅0,5+0,1⋅𝑝=0,1𝑝+0,39. Como 𝑃(𝑇𝑐) =0,395, 0,395=0,1𝑝+0,39⇔0,1𝑝=0,005⇔𝑝=0,05. Por tanto, la probabilidad de que un estudiante de la universidad C encuentre trabajo en su región es: 𝑃(𝑇|𝐶)=1−𝑃(𝑇𝑐|𝐶)=1−0,05=0,95.
  2. La probabilidad de que un estudiante proceda de la universidad A o B sabiendo que no ha encontrado trabajo en su región es: 𝑃(𝐴∪𝐵|𝑇𝑐)=𝑃((𝐴∪𝐵)∩𝑇𝑐)𝑃(𝑇𝑐)=𝑃((𝐴∩𝑇𝑐)∪(𝐵∩𝑇𝑐))𝑃(𝑇𝑐)=𝑃(𝐴∩𝑇𝑐)+𝑃(𝐵∩𝑇𝑐)𝑃(𝑇𝑐)==𝑃(𝐴)⋅𝑃(𝑇𝑐|𝐴)+𝑃(𝐵)⋅𝑃(𝑇𝑐|𝐵)𝑃(𝑇𝑐)=0,6⋅0,4+0,3⋅0,50,395=0,9873.

Ejercicio 6

Sean 𝐴 y 𝐵 dos sucesos del mismo espacio muestral tales que: 𝑃(𝐴∪𝐵)=37,𝑃(𝐴𝑐)=57y𝑃(𝐵𝑐)=23.

  1. ¿Son 𝐴 y 𝐵 independientes? ¿Son 𝐴 y 𝐵 incompatibles?
  2. Calcule 𝑃(𝐴𝑐 ∩𝐵𝑐).
  3. Calcule 𝑃(𝐵|𝐴𝑐).

Resolución

Sabemos que: 𝑃(𝐴𝑐)=57⇒𝑃(𝐴)=27y𝑃(𝐵𝑐)=23⇒𝑃(𝐵)=13.

  1. En primer lugar, calculamos la probabilidad de la intersección. Sabemos que la probabilidad de la unión viene dada por: 𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵). Así que, despejando en la expresión anterior, la probabilidad de la intersección es: 𝑃(𝐴∩𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∪𝐵)=27+13−37=421. Como 𝑃(𝐴 ∩𝐵) >0, los sucesos no son incompatibles. Por otro lado, observamos que: 𝑃(𝐴)⋅𝑃(𝐵)=27⋅13=221,𝑃(𝐴∩𝐵)=421. Como 𝑃(𝐴) ⋅𝑃(𝐵) ≠𝑃(𝐴 ∩𝐵), los sucesos no son independientes.
  2. Calculamos: 𝑃(𝐴𝑐∩𝐵𝑐)=𝑃((𝐴∪𝐵)𝑐)=1−𝑃(𝐴∪𝐵)=1−37=47.
  3. Calculamos: 𝑃(𝐵|𝐴𝑐)=𝑃(𝐵∩𝐴𝑐)𝑃(𝐴𝑐)=𝑃(𝐵)−𝑃(𝐴∩𝐵)𝑃(𝐴𝑐)=13−42157=15.

Ejercicio 7

Una fábrica de tornillos quiere hacer un estudio sobre la proporción de tornillos que cumplen las especificaciones del fabricante. Para ello ha seleccionado una muestra aleatoria de 1.500 tornillos, resultando que 1.425 cumplen las especificaciones del fabricante.

  1. Determine un intervalo de confianza para la proporción de tornillos que cumplen con las especificaciones del fabricante con un nivel de confianza del 97%.
  2. Manteniendo la proporción muestral y el nivel de confianza del apartado anterior, ¿cuál tendría que ser el tamaño mínimo de una nueva muestra para que el error de estimación sea inferior al 1%?

Resolución
  1. Como 1.425 tornillos de 𝑛 =1.500 han cumplido las especificaciones del fabricante, la proporción muestral es: 𝑝=1.4251.500=0,95. El intervalo de confianza para estimar la proporción poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(𝑝−𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛,𝑝+𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛). Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar la proporción de tornillos que cumplen las especificaciones del fabricante con un nivel de confianza del 97% es: 𝐼=(0,95−2,17⋅√0,95⋅(1−0,95)1.500,0,95+2,17⋅√0,95⋅(1−0,95)1.500)≈(0,9378;0,9622).
  2. El error máximo de estimación viene dado por: 𝐸=𝑧𝛼/2⋅√𝑝(1−𝑝)𝑛=2,17⋅√0,95⋅(1−0,95)𝑛=2,17⋅√0,0475𝑛. Si se quiere el error no sea mayor que 0,01, entonces: 2,17⋅√0,0475𝑛=0,01⇔√0,0475𝑛=0,012,17⇔0,0475𝑛=0,0122,172⇔𝑛=0,0475⋅2,1720,012=2.236,7275. Por tanto, el número mínimo de tornillos de la muestra debe ser 2.237.

Ejercicio 8

El número de días que los titulados en un cierto máster tardan en encontrar su primer trabajo sigue una distribución Normal de media 𝜇 desconocida y desviación típica 3 días.

  1. Se elige una muestra aleatoria de 100 titulados obteniéndose una media muestral de 8,1 días. Calcule un intervalo de confianza al 97% para estimar la media poblacional.
  2. Con un nivel de confianza del 92%, calcule el tamaño muestral mínimo necesario para que el error cometido, al estimar el número medio de días que estos titulados tardan en encontrar trabajo, sea inferior a un día.
  3. Suponiendo 𝜇 =7,61 días y tomando muestras aleatorias de 36 titulados, ¿qué distribución de probabilidad sigue la variable aleatoria media muestral? ¿Cuál es la probabilidad de que la media muestral sea superior a 8 días?

Resolución
  1. El intervalo de confianza para estimar la media poblacional con nivel de confianza 1 −𝛼 viene dado por: 𝐼=(――𝑥−𝑧𝛼/2⋅𝜎√𝑛,――𝑥+𝑧𝛼/2⋅𝜎√𝑛). Como el nivel de confianza es del 97%, entonces: 𝛼=1−0,97=0,03⇒1−𝛼2=1−0,032=0,985⇒𝑧𝛼/2=2,17. Por tanto, el intervalo de confianza para estimar el número medio de días que los titulados en un cierto máster tardan en encontrar su primer trabajo con un nivel de confianza del 97% es: 𝐼=(8,1−2,17⋅3√100,8,1+2,17⋅3√100)=(7,449;8,751).
  2. Si el nivel de confianza es del 92%, entonces: 𝛼=1−0,92=0,08⇒1−𝛼2=1−0,082=0,96⇒𝑧𝛼/2=1,75. El error máximo cometido viene dado por: 𝐸=𝑧𝛼/2⋅𝜎√𝑛=1,75⋅3√𝑛=5,25√𝑛. Si se quiere que el error máximo sea menor que 1, entonces: 5,25√𝑛=1⇔√𝑛=5,25⇔𝑛=5,252=27,5625. Por tanto, el tamaño mínimo de la muestra debe ser de 28 personas.
  3. La distribución de la media muestral ――𝑋 sigue una normal 𝑁(𝜇,𝜎√𝑛) con 𝜇 =7,61, 𝜎 =3 y 𝑛 =36. Es decir, ――𝑋 ∼𝑁(7,61; 0,5). La probabilidad de que la media muestral sea superior a 8 días es: 𝑃(――𝑋>8)=𝑃(𝑍>8−7,610,5)=𝑃(𝑍>0,78)=1−𝑃(𝑍≤0,78)≈0,2177.