Ejercicio 1
Calcula
Resolución
Calculamos el límite.
Calcula
Calculamos el límite.
Calcula los vértices y el área del rectángulo de área máxima inscrito en el recinto limitado por la gráfica de la función
La función 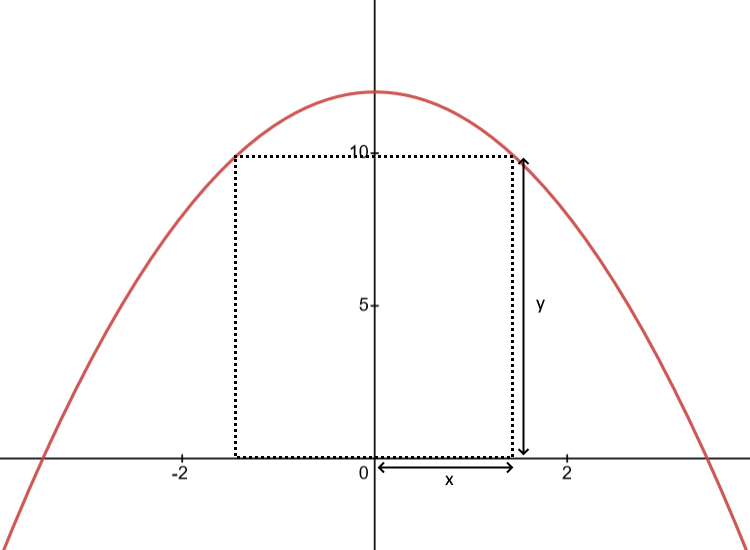
Como la base del rectángulo es
En primer lugar, calculamos la derivada de la función
Comprobamos que en el punto de abscisa
Así que el rectángulo tiene base
Calcula
Hacemos el cambio de variable
Hallamos en primer lugar una primitiva de la función aplicando el cambio de variable.
Por último, calculamos la integral definida mediante la regla de Barrow.
Considera las funciones
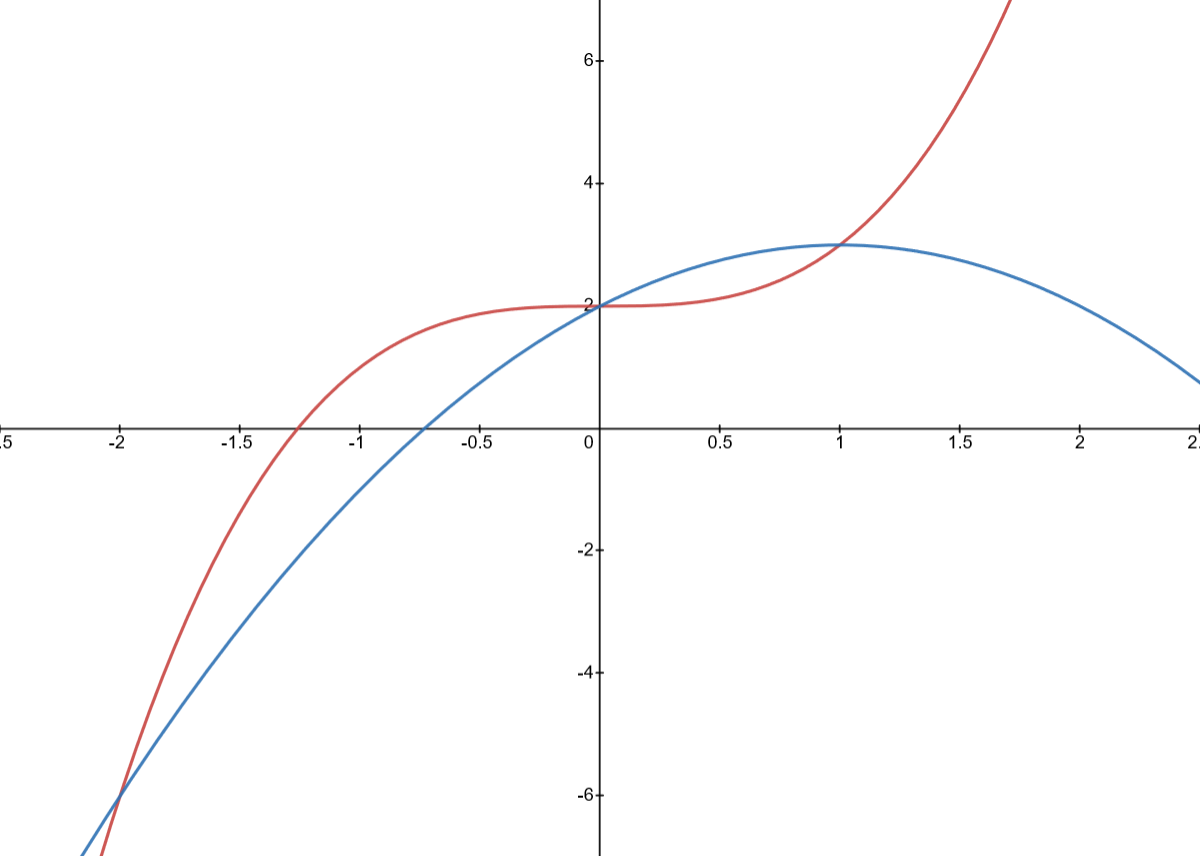
Considera las matrices
Se sabe que
Consideramos las rectas
Sean el plano