Ejercicios de ciencias

Ejercicio 2: Reserva 4 de 2025

Un náufrago se encuentra en una isla situada en el punto de coordenadas $(2, 0)$ de un plano. Se sabe que un ferry navega en el mismo plano siempre en la trayectoria dada por la gráfica de la función $𝑓 (𝑥) = \sqrt 𝑥 + 1$ . ¿Hacia qué punto de la trayectoria debe nadar el náufrago para recorrer la menor distancia posible? Calcula dicha distancia.

Ejercicio 1: Reserva 3 de 2024

De entre todos los rectángulos de área 25 cm², determina las dimensiones de aquel en el que el producto de las longitudes de sus dos diagonales sea el menor posible.

Resolución

Llamamos $𝑥$ e $𝑦$ al largo y el ancho del rectángulo en centímetros, respectivamente. Como $𝑥$ e $𝑦$ son longitudes, $𝑥, 𝑦 > 0 .$

Como el área del rectángulo es de 25 cm², entonces: $𝑥 𝑦 = 25 \Rightarrow 𝑦 = 25 𝑥 .$ Así que la función a minimizar es: $𝑓 (𝑥) = (\sqrt 𝑥 2 + 𝑦 2) 2 = 𝑥 2 + 𝑦 2 = 𝑥 2 + (25 𝑥) 2 = 𝑥 2 + 625 𝑥 2 .$

En primer lugar, hallamos la derivada de la función $𝑓 .$ $𝑓' (𝑥) = 2 𝑥 - 2 \cdot 625 𝑥 3 = 2 (𝑥 - 625 𝑥 3) .$ Hallamos los puntos críticos de $𝑓$ igualando la derivada a cero. $𝑓' (𝑥) = 0 \Leftrightarrow 2 (𝑥 - 625 𝑥 3) = 0 \Leftrightarrow 𝑥 - 625 𝑥 3 = 0 \Leftrightarrow 𝑥 4 = 625 \Leftrightarrow 𝑥 = \pm 5 .$ Como $𝑥 > 0$ por ser una longitud, la solución $𝑥 = - 5$ no es válida para este problema.

Comprobamos que en el punto de abscisa $𝑥 = 5$ se alcanza el mínimo de la función.

	$(0, 5)$	$(5, + \infty)$
signo de $𝑓'$	$-$	$+$
monotonía de $𝑓$	$\to$	$\to$

Luego $𝑓$ tiene un mínimo en $𝑥 = 5 .$ Por tanto, $𝑦 = 255 = 5 .$

Así que el rectángulo tiene base 5 cm y altura 5 cm, es decir, se trata de un cuadrado de lado 5 cm.

Ejercicio 1: Reserva 1 de 2023

Determina las longitudes de los lados de un rectángulo de área máxima que está inscrito en una semicircunferencia de 6 cm de radio, teniendo uno de sus lados sobre el diámetro de ella.

Resolución

La semicircunferencia es simétrica, así que todo rectángulo inscrito en ella estará centrado. Llamamos 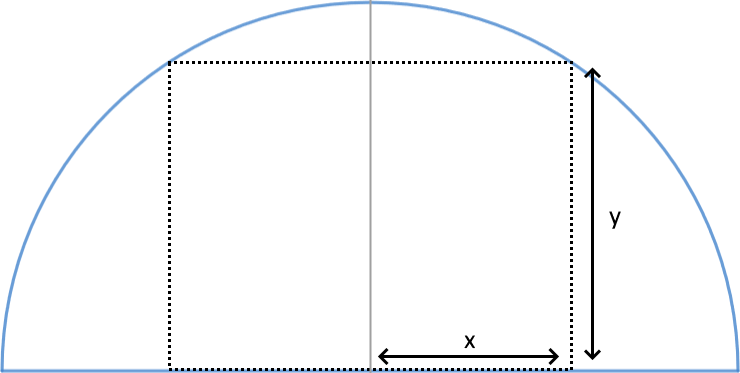$𝑥$ a la distancia en centímetros del centro a cada uno de los extremos del rectángulo horizontalmente. Por otro lado, llamamos $𝑦$ a la altura en centímetros del rectángulo. Como $𝑥$ e $𝑦$ son distancias no nulas, entonces $𝑥, 𝑦 > 0 .$ Representamos la figura. Figura

Como la base del rectángulo es $2 𝑥$ , entonces el área viene dada por $2 𝑥 𝑦 .$ Como además la mitad del rectángulo forma un triángulo rectángulo con hipotenusa de 6 cm, entonces $𝑥 2 + 𝑦 2 = 62 \Rightarrow 𝑦 = \sqrt 36 - 𝑥 2 .$ Por tanto, la función a maximizar es $𝑓 (𝑥) = 2 𝑥 \cdot 𝑦 = 2 𝑥 \cdot \sqrt 36 - 𝑥 2 = \sqrt 4 𝑥 2 (36 - 𝑥 2) = \sqrt 144 𝑥 2 - 4 𝑥 4 .$

En primer lugar, calculamos la derivada de la función $𝑓 .$ $𝑓' (𝑥) = 288 𝑥 - 16 𝑥 3 2 \sqrt 144 𝑥 2 - 4 𝑥 4 = 144 𝑥 - 8 𝑥 3 \sqrt 144 𝑥 2 - 4 𝑥 4 .$ Hallamos los puntos críticos de $𝑓$ igualando la derivada a cero. $𝑓' (𝑥) = 0 \Leftrightarrow 144 𝑥 - 8 𝑥 3 \sqrt 144 𝑥 2 - 4 𝑥 4 = 0 \Leftrightarrow 144 𝑥 - 8 𝑥 3 = 0 \Leftrightarrow 8 𝑥 (18 - 𝑥 2) = 0 \Leftrightarrow {𝑥 = 0, 18 - 𝑥 2 = 0 \Leftrightarrow 𝑥 = \pm \sqrt 18 = \pm 3 \sqrt 2 .$ Como $𝑥 > 0$ por ser una distancia no nula, las soluciones $𝑥 = 0$ y $𝑥 = - 3 \sqrt 2$ no son válidas para este problema.

Comprobamos que en el punto de abscisa $𝑥 = 3 \sqrt 2$ se alcanza el máximo de la función.

	$(0, 3 \sqrt 2)$	$(3 \sqrt 2, + \infty)$
signo de $𝑓'$	$+$	$-$
monotonía de $𝑓$	$\to$	$\to$

Luego $𝑓$ tiene un máximo en $𝑥 = 3 \sqrt 2 .$ Por tanto, $𝑦 = \sqrt 36 - 𝑥 2 = \sqrt 18 = 3 \sqrt 2 .$

Así que el rectángulo tiene base $6 \sqrt 2$ cm y altura $3 \sqrt 2$ cm.

Ejercicio 1: Reserva 2 de 2023

Halla dos números mayores o iguales que 0, cuya suma sea 1, y el producto de uno de ellos por la raíz cuadrada del otro sea máximo.

Resolución

Llamamos $𝑥$ e $𝑦$ a los dos números, con $𝑥, 𝑦 \geq 0 .$ Como $𝑥 + 𝑦 = 1$ , entonces $𝑦 = 1 - 𝑥 .$ Así que la función a maximizar es $𝑓 (𝑥) = 𝑥 \cdot \sqrt 𝑦 = 𝑥 \sqrt 1 - 𝑥 .$

En primer lugar, calculamos la derivada de la función $𝑓 .$ $𝑓' (𝑥) = \sqrt 1 - 𝑥 - 𝑥 2 \sqrt 1 - 𝑥 .$ Hallamos los puntos críticos de $𝑓$ igualando la derivada a cero. $𝑓' (𝑥) = 0 \Leftrightarrow \sqrt 1 - 𝑥 - 𝑥 2 \sqrt 1 - 𝑥 = 0 \Leftrightarrow 1 - 𝑥 = 𝑥 2 \Leftrightarrow 𝑥 = 23 .$

Comprobamos que en el punto de abscisa $𝑥 = 23$ se alcanza el máximo de la función.

	$(0, 23)$	$(23, 1)$
signo de $𝑓'$	$+$	$-$
monotonía de $𝑓$	$\to$	$\to$

Luego $𝑓$ tiene un máximo en $𝑥 = 23 .$

Por tanto, los números son $𝑥 = 23$ e $𝑦 = 1 - 𝑥 = 13 .$

Ejercicio 1: Reserva 3 de 2023

De entre todos los rectángulos de diagonal 10 cm (cada una), calcula las dimensiones del que tiene mayor área.

Resolución

Llamamos $𝑥$ e $𝑦$ al largo y al ancho del rectángulo en centímetros, respectivamente. Como $𝑥$ e $𝑦$ son distancias, entonces $𝑥, 𝑦 \geq 0 .$

Como la diagonal es la hipotenusa de un triángulo rectángulo y mide 10 cm, entonces $𝑥 2 + 𝑦 2 = 102 \Rightarrow 𝑦 = \sqrt 100 - 𝑥 2 .$ Así que la función a maximizar es $𝑓 (𝑥) = 𝑥 \cdot 𝑦 = 𝑥 \sqrt 100 - 𝑥 2 .$

En primer lugar, calculamos la derivada de la función $𝑓 .$ $𝑓' (𝑥) = \sqrt 100 - 𝑥 2 - 𝑥 2 \sqrt 100 - 𝑥 2 .$ Hallamos los puntos críticos de $𝑓$ igualando la derivada a cero. $𝑓' (𝑥) = 0 \Leftrightarrow \sqrt 100 - 𝑥 2 - 𝑥 2 \sqrt 100 - 𝑥 2 = 0 \Leftrightarrow 100 - 𝑥 2 = 𝑥 2 \Leftrightarrow 100 = 2 𝑥 2 \Leftrightarrow 𝑥 2 = 50 \Leftrightarrow 𝑥 = \pm \sqrt 50 .$ Como $𝑥 \geq 0$ por ser una distancia, la solución $𝑥 = - \sqrt 50$ no es válida para este problema.

Comprobamos que en el punto de abscisa $𝑥 = \sqrt 50$ se alcanza el máximo de la función.

	$(0, \sqrt 50)$	$(\sqrt 50, + \infty)$
signo de $𝑓'$	$+$	$-$
monotonía de $𝑓$	$\to$	$\to$

Luego $𝑓$ tiene un máximo en $𝑥 = \sqrt 50 .$ Por tanto, $𝑦 = \sqrt 100 - 𝑥 2 = \sqrt 50 .$

Así que el rectángulo tiene base $\sqrt 50$ cm y altura $\sqrt 50$ cm, es decir, se trata de un cuadrado de lado $\sqrt 50$ cm.

Ejercicio 2: Reserva 4 de 2023

En una fábrica de pinturas, las latas que se utilizan para envasar la pintura tienen forma cilíndrica y una capacidad de 20 litros. Halla las dimensiones del cilindro, con tapas, para que la chapa empleada en su contrucción sea mínima.

Resolución

Las dimensiones de un cilindro vienen dadas por el radio de su base y la altura. Llamamos $𝑟$ y $ℎ$ al radio y la altura en centímetros de la lata, respectivamente. Como $𝑟$ y $ℎ$ son distancias, $𝑟, ℎ \geq 0 .$

Como las latas tienen una capacidad de 20 litros, es decir, 20.000 cm³, entonces $𝜋 𝑟 2 ℎ = 20.000 \Leftrightarrow ℎ = 20.000 𝜋 𝑟 2 .$ Así que la función a minimizar es $𝑓 (𝑟) = 2 𝜋 𝑟 2 + 2 𝜋 𝑟 ℎ = 2 𝜋 𝑟 2 + 2 𝜋 20.000 𝑟 𝜋 𝑟 2 = 2 𝜋 𝑟 2 + 40.000 𝑟 .$

En primer lugar, calculamos la derivada de la función $𝑓 .$ $𝑓' (𝑟) = 4 𝜋 𝑟 - 40.000 𝑟 2 .$ Hallamos los puntos críticos de $𝑓$ igualando su derivada a cero. $𝑓' (𝑟) = 0 \Leftrightarrow 4 𝜋 𝑟 - 40.000 𝑟 2 = 0 \Leftrightarrow 4 𝜋 𝑟 = 40.000 𝑟 2 \Leftrightarrow 𝑟 3 = 10.000 𝜋 \Leftrightarrow 𝑟 = 3 \sqrt 10.000 𝜋 \approx 14, 71 .$ Comprobamos que en el punto de abscisa $𝑟 = 3 \sqrt 10.000 𝜋$ se alcanza el mínimo de la función.

	$(0, 3 \sqrt 10.000 𝜋)$	$(3 \sqrt 10.000 𝜋, + \infty)$
signo de $𝑓'$	$-$	$+$
monotonía de $𝑓$	$\to$	$\to$

Luego $𝑓$ tiene un mínimo en $𝑟 = 3 \sqrt 10.000 𝜋 .$ Por tanto, $ℎ = 20.000 𝜋 𝑟 2 = 20.000 𝜋 (𝜋 10.000) 2 / 3 \approx 29, 42 .$

Así que las latas deben tener un radio de 14,71 cm y una altura de 29,42 cm.

Ejercicio 2: Junio de 2022

De entre todos los rectángulos con lados paralelos a los ejes de coordenadas, determina las dimensiones de aquel de área máxima que puede inscribirse en la región limitada por las gráficas de las funciones $𝑓, 𝑔 : ℝ \to ℝ$ , definidas por $𝑓 (𝑥) = 4 - 𝑥 2 3 y 𝑔 (𝑥) = 𝑥 2 6 - 2 .$

Resolución

Las funciones $𝑓$ y $𝑔$ tienen simetría par, así que todo rectángulo inscrito en el recinto limitado por sus gráficas estará centrado con respecto al eje de ordenadas. Llamamos $𝑥$ a la distancia del centro a cada uno de los extremos del rectángulo horizontalmente. Por otro lado, llamamos $𝑦$ a la altura del rectángulo. Como $𝑥$ e $𝑦$ son distancias, entonces $𝑥, 𝑦 \geq 0 .$ Representamos la figura. Figura

Como la base del rectángulo es $2 𝑥$ , entonces el área viene dada por $2 𝑥 𝑦 .$ Como además los vértices están sobre las gráficas de $𝑓$ y $𝑔$ , entonces $𝑦 = 𝑓 (𝑥) - 𝑔 (𝑥) = 4 - 𝑥 2 3 - (𝑥 2 6 - 2) = - 𝑥 2 2 + 6 .$ Por tanto, la función a maximizar es $ℎ (𝑥) = 2 𝑥 \cdot 𝑦 = 2 𝑥 \cdot (- 𝑥 2 2 + 6) = - 𝑥 3 + 12 𝑥 .$

En primer lugar, calculamos la derivada de la función $ℎ .$ $ℎ' (𝑥) = - 3 𝑥 2 + 12 .$ Hallamos los puntos críticos de $ℎ$ igualando la derivada a cero. $ℎ' (𝑥) = 0 \Leftrightarrow - 3 𝑥 2 + 12 = 0 \Leftrightarrow 𝑥 2 = 4 \Leftrightarrow 𝑥 = \pm 2 .$ Como $𝑥 \geq 0$ por ser una distancia, la solución $𝑥 = - 2$ no es válida para este problema.

Comprobamos que en el punto de abscisa $𝑥 = 2$ se alcanza el máximo de la función.

	$(0, 2)$	$(2, + \infty)$
signo de $ℎ'$	$+$	$-$
monotonía de $ℎ$	$\to$	$\to$

Luego $𝑆$ tiene un máximo en $𝑥 = 2 .$ Por tanto, $𝑦 = - 𝑥 2 2 + 6 = 4 .$

Así que el rectángulo tiene base $4 𝑢$ y altura $4 𝑢$ , es decir, se trata de un cuadrado de lado $4 𝑢 .$

Ejercicio 2: Reserva 1 de 2022

Se quiere cercar un trozo de terreno como el de la figura, de modo que el área del recinto central rectangular sea de $200 𝜋$ metros cuadrados. Sabiendo que el coste de la cerca que se puede poner en los tramos rectos es de 10 euros por metro lineal, y en los tramos circulares de 20 euros por metro lineal, calcula las dimensiones $𝑎$ y $𝑏$ del terreno para los que se minimiza el coste del cercado. Figura

Resolución

El área del recinto rectangular es de $200 𝜋$ metros cuadrados, así que $𝑎 𝑏 = 200 𝜋 \Rightarrow 𝑏 = 200 𝜋 𝑎 .$ La longitud de cerca en los tramos rectos es de $2 𝑎$ y en los tramos circulares de $2 𝜋 𝑏 2 = 𝜋 𝑏 .$ Como además los costes son de 10€ y 20€ por metro en los tramos rectos y circulares, respectivamente, la función a minimizar es $𝑓 (𝑎) = 10 \cdot 2 𝑎 + 20 \cdot 𝜋 𝑏 = 20 𝑎 + 20 𝜋 \cdot 200 𝜋 𝑎 = 20 𝑎 + 4.000 𝑎 .$

En primer lugar, calculamos la derivada de la función $𝑓 .$ $𝑓' (𝑎) = 20 - 4.000 𝑎 2 .$ Hallamos los puntos críticos de $𝑓$ igualando la derivada a cero. $𝑓' (𝑎) = 0 \Leftrightarrow 20 - 4.000 𝑎 2 = 0 \Leftrightarrow 20 = 4.000 𝑎 2 \Leftrightarrow 20 𝑎 2 = 4.000 \Leftrightarrow 𝑎 2 = 200 \Leftrightarrow 𝑎 = \sqrt 200 .$

Comprobamos que en el punto de abscisa $𝑎 = \sqrt 200$ se alcanza el mínimo de la función.

	$(- \infty, \sqrt 200)$	$(\sqrt 200, + \infty)$
signo de $𝑓'$	$-$	$+$
monotonía de $𝑓$	$\to$	$\to$

Luego $𝑓$ tiene un mínimo en $𝑎 = \sqrt 200 .$ Por tanto, $𝑏 = 200 𝜋 𝑎 = 200 𝜋 \sqrt 200 = \sqrt 200 𝜋 .$

Así que $𝑎 = \sqrt 200$ m y $𝑏 = \sqrt 200 𝜋$ m.

Ejercicio 2: Julio de 2022

Calcula los vértices y el área del rectángulo de área máxima inscrito en el recinto limitado por la gráfica de la función $𝑓 : ℝ \to ℝ$ definida por $𝑓 (𝑥) = - 𝑥 2 + 12$ y el eje de abscisas, y que tiene su base sobre dicho eje.

Resolución

La función 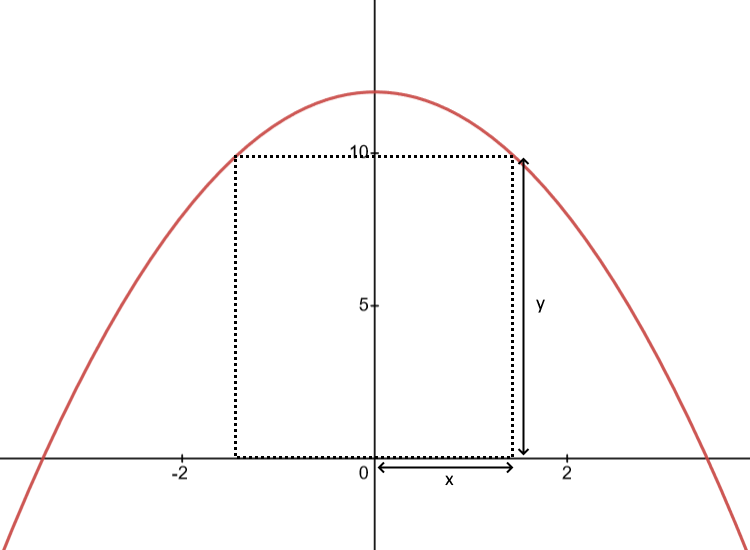$𝑓 (𝑥) = - 𝑥 2 + 12$ es simétrica par, así que todo rectángulo inscrito en el recinto limitado por su gráfica y el eje de abscisas estará centrado con respecto al eje de ordenadas. Llamamos $𝑥$ a la distancia del centro a cada uno de los extremos del rectángulo horizontalmente. Por otro lado, llamamos $𝑦$ a la altura del rectángulo. Como $𝑥$ e $𝑦$ son distancias, entonces $𝑥, 𝑦 \geq 0 .$ Representamos la figura. Figura

Como la base del rectángulo es $2 𝑥$ , el área viene dada por $2 𝑥 𝑦 .$ Como además los vértices superiores del rectángulos están sobre la gráfica de la función $𝑓$ , entonces $𝑦 = 𝑓 (𝑥) = - 𝑥 2 + 12 .$ Por tanto, la función a maximizar es $𝑔 (𝑥) = 2 𝑥 \cdot 𝑦 = 2 𝑥 \cdot (- 𝑥 2 + 12) = - 2 𝑥 3 + 24 𝑥 .$

En primer lugar, calculamos la derivada de la función $𝑔 .$ $𝑔' (𝑥) = - 6 𝑥 2 + 24 .$ Hallamos los puntos críticos de $𝑔$ igualando la derivada a cero. $𝑔' (𝑥) = 0 \Leftrightarrow - 6 𝑥 2 + 24 = 0 \Leftrightarrow 𝑥 2 = 4 \Leftrightarrow 𝑥 = \pm 2 .$ Como $𝑥 \geq 0$ por ser una distancia, la solución $𝑥 = - 2$ no es válida para este problema.

Comprobamos que en el punto de abscisa $𝑥 = 2$ se alcanza el máximo de la función.

	$(0, 2)$	$(2, + \infty)$
signo de $𝑔'$	$+$	$-$
monotonía de $𝑔$	$\to$	$\to$

Luego $𝑔$ tiene un máximo en $𝑥 = 2 .$ Por tanto, $𝑦 = - 𝑥 2 + 12 = 8 .$

Así que el rectángulo tiene base $4 𝑢$ y altura $8 𝑢$ , por lo que su área es $4 \cdot 8 = 32 𝑢 2 .$ Además, sus vértices son $(2, 0)$ , $(- 2, 0)$ , $(2, 8)$ y $(- 2, 8) .$

Ejercicio 5: Reserva 1 de 2020

Una familia desea acotar una zona rectangular en el jardín de su casa para dedicarla al cultivo ecológico. Para ello dispone de 96 metros de valla, pero necesita dejar una abertura de 4 metros en uno de los laterales para instalar una puerta. Determina las dimensiones de la zona rectangular de área máxima que puede acotarse de esta manera y el valor de dicha área.

Resolución

Llamamos $𝑥$ e $𝑦$ al largo y al ancho de la zona rectangular en metros, respectivamente. Como $𝑥$ e $𝑦$ son distancias, entonces $𝑥, 𝑦 \geq 0 .$

Como se dispone de 96 metros de valla y se deja una abertura de 4 metros, entonces el perímetro debe ser de 100 metros. Es decir, $2 𝑥 + 2 𝑦 = 100 \Leftrightarrow 𝑥 + 𝑦 = 50 \Leftrightarrow 𝑦 = 50 - 𝑥 .$ Así que la función a maximizar es: $𝑓 (𝑥) = 𝑥 \cdot 𝑦 = 𝑥 (50 - 𝑥) = 50 𝑥 - 𝑥 2 .$

En primer lugar, calculamos la derivada de la función $𝑓 .$ $𝑓' (𝑥) = 50 - 2 𝑥 .$ Hallamos los puntos críticos de $𝑓$ igualando la derivada a cero. $𝑓' (𝑥) = 0 \Leftrightarrow 50 - 2 𝑥 = 0 \Leftrightarrow 50 = 2 𝑥 \Leftrightarrow 𝑥 = 25 .$

Comprobamos que en el punto de abscisa $𝑥 = 25$ se alcanza el máximo de la función.

	$(0, 25)$	$(25, + \infty)$
signo de $𝑓'$	$+$	$-$
monotonía de $𝑓$	$\to$	$\to$

Luego $𝑓$ tiene un máximo en $𝑥 = 25 .$ Por tanto, $𝑦 = 50 - 𝑥 = 25 .$

Así que la zona rectangular tiene base 25 m y altura 25 m, es decir, se trata de una zona cuadrada de lado 25 m. Por tanto, su área es de 625 m².

Ejercicio A1: Septiembre de 2019

Dada la función $𝑓 : ℝ \to ℝ$ definida por $𝑓 (𝑥) = 6 - 16 𝑥 2$ , calcula las dimensiones del rectángulo de área máxima, de lados paralelos a los ejes, inscrito en el recinto comprendido entre la gráfica de $𝑓$ y la recta $𝑦 = 0 .$

Ejercicio A1: Reserva 1 de 2018

Se desea construir un rectángulo, como el de la figura, de área máxima. La base está situada sobre el eje 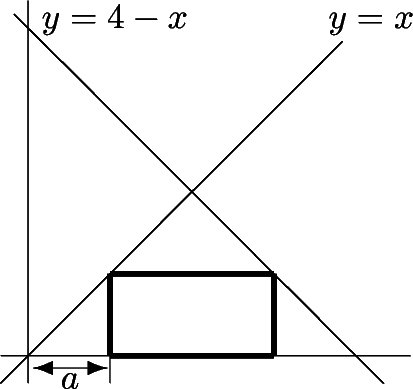$𝑂 𝑋$ , un vértice está en la recta $𝑦 = 𝑥$ y el otro, en la recta $𝑦 = 4 - 𝑥 .$ Figura Se pide:

Halla la altura del rectángulo en función de $𝑎 .$
Halla la base del rectángulo en función de $𝑎 .$
Encuentra el valor de $𝑎$ que hace máximo el área del rectángulo.

Ejercicio A1: Reserva 2 de 2018

Se desea construir una canaleta, para la recogida de agua, cuya sección es como la de la figura. La base y los costados deben medir 10 cm y se trata de darle la inclinación adecuada a los costados para obtener una sección de área máxima. 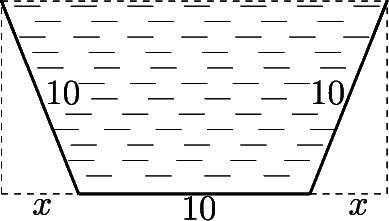Figura Se pide:

Halla la altura de la canaleta en función de $𝑥 .$
Halla el área de la sección de la canaleta en función de $𝑥 .$
Encuentra el valor de $𝑥$ que hace máximo dicho área.

Ejercicio A1: Reserva 3 de 2018

Considera un triángulo isósceles en el que el lado desigual mide 8 cm y la altura correspondiente mide 5 cm. Calcula las dimensiones del rectángulo de área máxima que se puede inscribir en dicho triángulo.

Ejercicio B1: Reserva 4 de 2018

Se desea construir una caja sin tapadera de base cuadrada. El precio del material es de 18 euros/m² para los laterales y de 24 euros/m² para la base. Halla las dimensiones de la caja de mayor volumen que se puede construir si disponemos de 50 euros.

Ejercicio A1: Junio de 2017

Se quiere hacer una puerta rectangular coronada por un semicírculo como el de la figura. El hueco de la puerta tiene que tener 16 metros cuadrados. Figura Si es posible, determina la base $𝑥$ para que el perímetro sea mínimo.

Ejercicio B1: Reserva 2 de 2017

Una cuerda de un metro de longitud se divide en dos trozos con los que se construyen un cuadrado y una circunferencia respectivamente. Determina, si es posible, las longitudes de los trozos para que la suma de las áreas sea mínima.

Ejercicio A1: Reserva 3 de 2017

Se necesita construir un depósito cilíndrico, con tapas inferior y superior, con capacidad de $20 𝜋$ m³. El material para las tapas cuesta 10 euros cada m² y el material para el resto del cilindro 8 euros cada m². Calcula, si existe, el radio de las tapas y la altura del cilindro que hace que el coste total sea mínimo.

Ejercicio A1: Septiembre de 2017

Una imprenta recibe un encargo para realizar una tarjeta rectangular con las siguientes características: la superficie rectangular que debe ocupar la zona impresa debe ser de 100 cm², el margen superior tiene que ser de 2 cm, el inferior de 3 cm y los laterales de 5 cm cada uno. Calcula, si es posible, las dimensiones que debe tener la tarjeta de forma que se utilice la menor cantidad de papel posible.

Ejercicio B1: Reserva 1 de 2016

Se dispone de un cartón cuadrado de 50 cm de lado para construir una caja sin tapadera a partir del cartón. Para ello, se corta un cuadrado de $𝑥$ cm de lado en cada una de las esquinas. Halla el valor de $𝑥$ para que el volumen de la caja sea máximo y calcula dicho volumen.

Ejercicio B1: Reserva 3 de 2016

De un terreno se desea vender un solar rectangular de 12800 m² dividido en 3 parcelas iguales como las que aparecen en el dibujo. Se quieren vallar las lindes de las tres parcelas (los bordes y las separaciones de las parcelas). Figura Determina las dimensiones del solar y de cada una de las tres parcelas para que la longitud de la valla utilizada sea mínima.

Ejercicio A1: Reserva 4 de 2016

Se quiere construir un bote de conservas cilíndrico, con tapa, de un litro de capacidad. Calcula las dimensiones del bote para que en su construcción se utilice la menor cantidad posible de hojalata.

Ejercicio A1: Junio de 2015

Se quiere construir un depósito abierto de base cuadrada y paredes verticales con capacidad para 13,5 metros cúbicos. Para ello se dispone de una chapa de acero con grosor uniforme. Calcula las dimensiones del depósito para que el gasto en chapa sea el mínimo posible.

Ejercicio A1: Reserva 1 de 2015

Se quiere vallar un campo rectangular que está junto a un camino. Si la valla del lado del camino cuesta 80 euros/metro y la de los otros lados 10 euros/metro, halla las dimensiones del campo de área máxima que puede vallarse con 28.800 euros.

Ejercicio B1: Reserva 3 de 2015

Queremos fabricar una caja con base cuadrada, de tal manera que la altura de la caja más el perímetro de la base sumen 60 cm. Determina sus dimensiones para que contenga el mayor volumen posible.

Ejercicio B1: Septiembre de 2015

Un granjero desea vallar un terreno rectangular de pasto adyacente a un río. El terreno debe tener 180.000 m² para producir suficiente pasto para su ganado. ¿Qué dimensiones tendrá el terreno rectangular de modo que utilice la mínima cantidad de valla, si el lado que da al río no necesita vallado?

Ejercicio B1: Junio de 2014

Se desea construir un depósito en forma de cilindro recto, con base circular y sin tapadera, que tenga una capacidad de 125 m³. Halla el radio de la base y la altura que debe tener el depósito para que la superficie sea mínima.

Ejercicio A1: Reserva 4 de 2014

De entre todos los triángulos rectángulos de área 8 cm², determina las dimensiones del que tiene la hipotenusa de menor longitud.

Ejercicio B1: Septiembre de 2014

De todos los números reales positivos, determina el que sumado con su inverso da suma mínima.

Ejercicio A1: Reserva 2 de 2013

Un rectángulo está inscrito en un semicírculo de $\sqrt 5$ cm de radio, de forma que uno de sus lados está contenido en el diámetro del semicírculo y el lado opuesto tiene sus vértices sobre la semicircunferencia. Calcula las dimensiones del rectángulo sabiendo que es el de mayor perímetro posible.

Ejercicio A1: Reserva 4 de 2013

Halla las dimensiones del rectángulo de área máxima inscrito en un triángulo isósceles de 6 metros de base (el lado desigual) y 4 metros de alto.

Ejercicio A1: Septiembre de 2013

Un alambre de 10 metros de longitud se divide en dos trozos. Con uno de ellos se forma un triángulo equilátero y con el otro un cuadrado. Halla la longitud de dichos trozos para que la suma de las áreas sea mínima.

Ejercicio A1: Reserva 3 de 2012

Un alambre de longitud 2 metros se divide en dos trozos. Con el primero se forma un rectángulo cuya base es el doble de su altura y con el segundo trozo se forma un cuadrado. Calcula las longitudes de dichos trozos para que la suma de las áreas del rectángulo y el cuadrado resultantes sea mínima.

Ejercicio B1: Reserva 4 de 2012

De entre todos los triángulos rectángulos de hipotenusa 10 unidades, determina las dimensiones del de área máxima.

Ejercicio A1: Junio de 2011

Se desea construir un depósito cilíndrico cerrado de área total igual a 54 m². Determina el radio de la base y la altura del cilindro para que este tenga volumen máximo.

Ejercicio A1: Reserva 1 de 2011

Un alambre de 100 m de longitud se divide en dos trozos. Con uno de los trozos se construye un cuadrado y con el otro un rectángulo cuya base es doble que su altura. Calcula las longitudes de cada uno de los trozos con la condición de que la suma de las áreas de estas dos figuras sea mínima.

Ejercicio A1: Reserva 2 de 2011

Una ventana normanda consiste en un rectángulo coronado con un semicírculo. Figura De entre todas las ventanas normandas de perímetro 10 m, halla las dimensiones del marco de la de área máxima.

Ejercicio B1: Reserva 3 de 2011

En el primer cuadrante representamos un rectángulo de tal manera que tiene un vertice en el origen de coordenadas y el vertice opuesto en la parábola $𝑦 = - 𝑥 2 + 3$ . Determina las dimensiones del rectángulo para que su área sea máxima.

Ejercicio A1: Reserva 4 de 2011

Queremos hacer junto a la carretera un cercado rectangular para unos caballos en una zona llana. Cada metro del lado del cercado que está junto a la carretera nos cuesta 100 euros, mientras que para el resto del cercado nos cuesta 10 euros el metro. ¿Cuáles son las dimensiones del prado de área máxima que podemos cercar con 3.000 euros?

Ejercicio A1: Septiembre de 2011

Calcula la base y la altura del triángulo isósceles de perímetro 8 y de área máxima.

Ejercicio A1: Septiembre de 2010

Una hoja de papel tiene que contener 18 cm² de texto. Los márgenes superior e inferior han de tener 2 cm cada uno y los laterales 1 cm. Calcula las dimensiones de la hoja para que el gasto de papel sea mínimo.