Llamamos 𝑥 al número de litros del líquido 𝐿1, 𝑦 al número de litros de 𝐿2 y 𝑧 al número de litros de 𝐿3.
Se quiere obtener un litro de mezcla de 𝐿1, 𝐿2 y 𝐿3, así que
𝑥+𝑦+𝑧=1.
Como se pide que la cantidad de sodio en la mezcla sea de 100 mg y cada litro de 𝐿1, 𝐿2 y 𝐿3 contiene 120 mg, 100 mg y 60 mg de sodio, respectivamente, entonces
120𝑥+100𝑦+60𝑧=100.
Como también se pretende que la cantidad de magnesio en la mezcla sea de 100 mg y cada litro de 𝐿1, 𝐿2 y 𝐿3 contiene 90 mg, 90 mg y 180 mg de magnesio, respectivamente, entonces
90𝑥+90𝑦+180𝑧=100.
Por tanto, podemos plantear el sistema de ecuaciones lineales
⎧{
{⎨{
{⎩𝑥+𝑦+𝑧=1,120𝑥+100𝑦+60𝑧=100,90𝑥+90𝑦+180𝑧=100⇒⎧{
{⎨{
{⎩𝑥+𝑦+𝑧=1,6𝑥+5𝑦+3𝑧=5,9𝑥+9𝑦+18𝑧=10.
La matriz de coeficientes del sistema es
𝐴=⎛⎜
⎜
⎜⎝1116539918⎞⎟
⎟
⎟⎠.
Calculamos su determinante:
|𝐴|=∣1116539918∣=90+27+54−45−27−108=−9.
Como det(𝐴) ≠0, entonces rang(𝐴) =3.
El rango de la matriz de coeficientes es máximo, así que por el teorema de Rouché-Frobenius el sistema es compatible determinado.
Por tanto, sí es posible obtener dicha mezcla.
Resolvemos el sistema mediante el método de Gauss.
⎛⎜
⎜
⎜
⎜⎝11116535991810⎞⎟
⎟
⎟
⎟⎠𝐹2−6𝐹1←←←←←←←←←→𝐹3−9𝐹1⎛⎜
⎜
⎜
⎜⎝11110−1−3−10091⎞⎟
⎟
⎟
⎟⎠.
El sistema resultante es
⎧{
{⎨{
{⎩𝑥+𝑦+𝑧=1,−𝑦−3𝑧=−1,9𝑧=1.
Por tanto,
9𝑧=1⇔𝑧=19,−𝑦−3𝑧=−1𝑧=1/9←←←←←←←←→−𝑦−3⋅19=−1⇔𝑦=23,𝑥+𝑦+𝑧=1𝑦=2/3←←←←←←←←→𝑧=1/9𝑥+23+19=1⇔𝑥=29.
Así que la mezcla ha de estar formada por 29 litros de 𝐿1, 23 litros de 𝐿2 y 19 litros de 𝐿3.
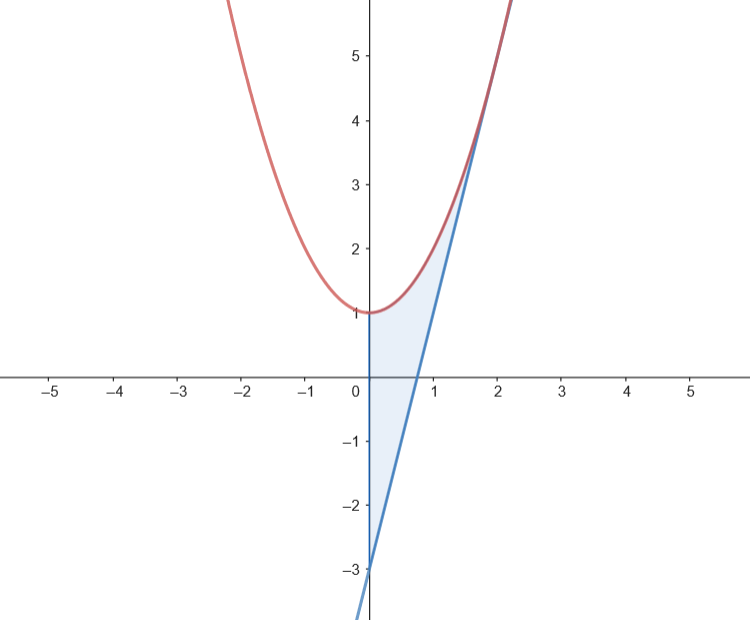 Calculamos el área del recinto.
Calculamos el área del recinto.