Ejercicio 4: Junio de 2025
Sean los puntos
- Halla los valores de
𝑚 𝑂 𝐴 𝐵 𝐶 - Para
𝑚 = 0 𝑂 𝐴 𝐵 𝐶
Resolución
-
El volumen del tetraedro determinado por los puntos
𝑂 𝐴 𝐵 𝐶 ⃗ 𝑂 𝐴 = ( 0 , 2 , − 2 ) ⃗ 𝑂 𝐵 = ( 1 , 2 , 𝑚 ) ⃗ 𝑂 𝐶 = ( 2 , 3 , 2 ) [ ⃗ 𝑂 𝐴 , ⃗ 𝑂 𝐵 , ⃗ 𝑂 𝐶 ] = ∣ 0 2 − 2 1 2 𝑚 2 3 2 ∣ = 4 𝑚 − 6 + 8 − 4 = 4 𝑚 − 2 ⇒ 𝑉 = | 4 𝑚 − 2 | 6 . | 4 𝑚 − 2 | 6 = 3 ⇔ | 4 𝑚 − 2 | = 1 8 ⇔ { 4 𝑚 − 2 = 1 8 ⇔ 4 𝑚 = 2 0 ⇔ 𝑚 = 5 , 4 𝑚 − 2 = − 1 8 ⇔ 4 𝑚 = − 1 6 ⇔ 𝑚 = − 4 . -
El plano
𝜋 𝐴 𝐵 𝐶 ⃗ 𝐴 𝐵 = ( 1 , 0 , 2 ) ⃗ 𝐴 𝐶 = ( 2 , 1 , 4 ) ⃗ 𝑛 𝜋 = ∣ ⃗ 𝑥 ⃗ 𝑦 ⃗ 𝑧 1 0 2 2 1 4 ∣ = ( − 2 , 0 , 1 ) . 𝐴 𝜋 𝜋 ≡ − 2 𝑥 + 𝑧 + 2 = 0 ⇔ 2 𝑥 − 𝑧 − 2 = 0 . 𝑂 𝜋 d i s t ( 𝑂 , 𝜋 ) = | − 2 | √ 5 = 2 √ 5 𝑢 .
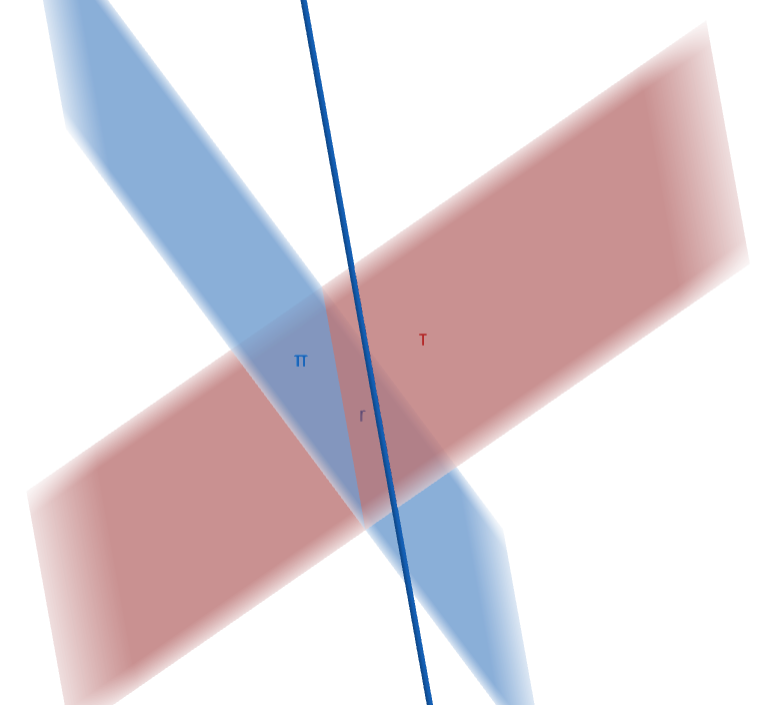 Como
Como 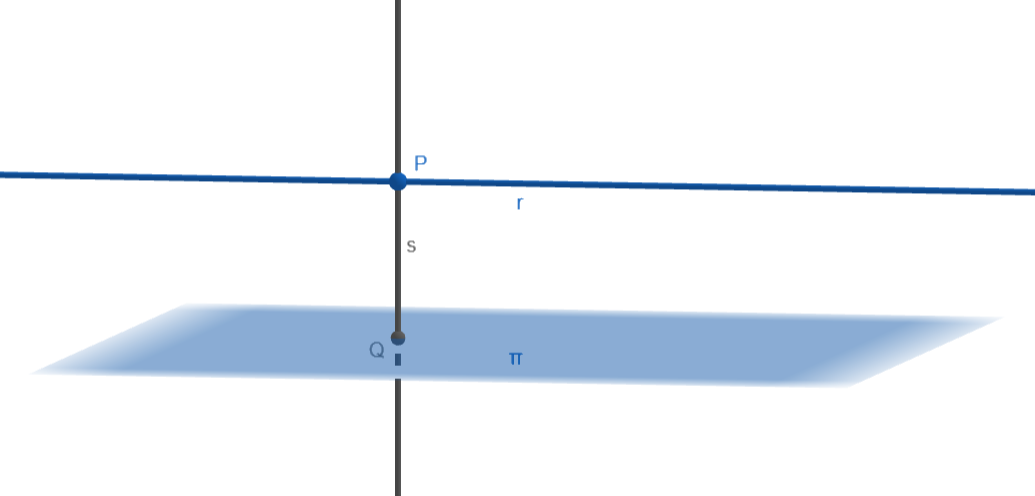 Si
Si 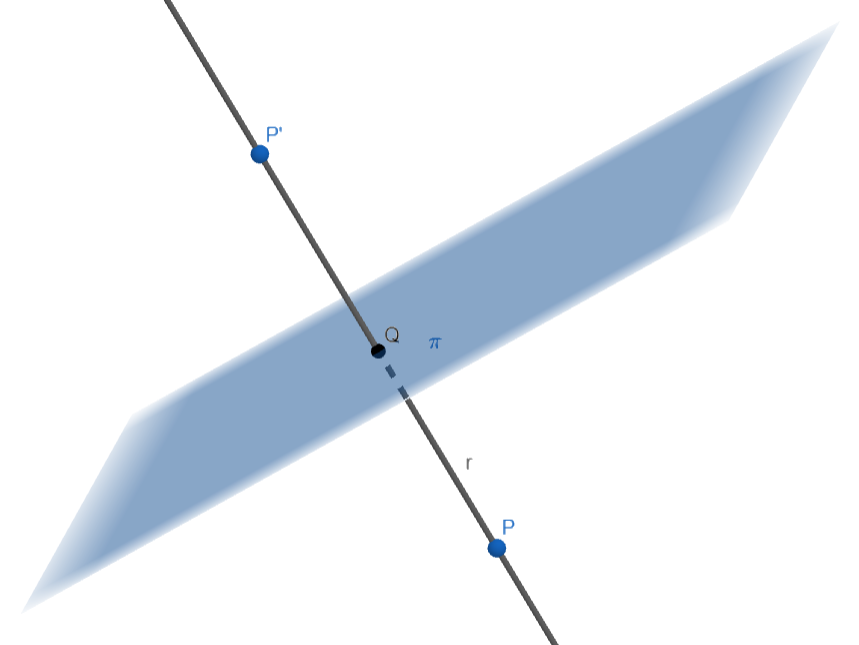 Al ser perpendicular a
Al ser perpendicular a