Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 3 de 2022

Ejercicio 1

Calcula 𝑎 y 𝑏 sabiendo que lím𝑥→0⁡𝑎sen⁡(𝑥)+𝑥ln⁡(𝑥+1)+𝑏𝑥2𝑥3+𝑥2=2.

Resolución

Calculamos el límite. lím𝑥→0⁡𝑎sen⁡(𝑥)+𝑥ln⁡(𝑥+1)+𝑏𝑥2𝑥3+𝑥2=00.

Para resolver la indeterminación, aplicamos la regla de L'Hôpital. lím𝑥→0⁡𝑎sen⁡(𝑥)+𝑥ln⁡(𝑥+1)+𝑏𝑥2𝑥3+𝑥2L’H=lím𝑥→0⁡𝑎cos⁡(𝑥)+ln⁡(𝑥+1)+𝑥𝑥+1+2𝑏𝑥3𝑥2+2𝑥=𝑎0. Si 𝑎 ≠0 este límite será infinito, así que necesariamente 𝑎 =0.

Continuamos resolviendo el límite para 𝑎 =0. lím𝑥→0⁡ln⁡(𝑥+1)+𝑥𝑥+1+2𝑏𝑥3𝑥2+2𝑥L’H=1𝑥+1+1(𝑥+1)2+2𝑏6𝑥+2=2+2𝑏2=1+𝑏.

Por tanto, lím𝑥→0⁡𝑎sen⁡(𝑥)+𝑥ln⁡(𝑥+1)+𝑏𝑥2𝑥3+𝑥2=2⇔1+𝑏=2⇔𝑏=1.

Ejercicio 2

Sea 𝑓 :[0,2𝜋] →ℝ la función definida por 𝑓(𝑥) =𝑒𝑥(cos⁡(𝑥) +sen⁡(𝑥)).

  1. Halla los extremos absolutos de 𝑓 (abscisas donde se obtienen y valores que se alcanzan).
  2. Determina la ecuación de la recta tangente y la ecuación de la recta normal a la gráfica de 𝑓 en el punto de abscisa 𝑥 =3𝜋2.

Resolución
  1. En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=𝑒𝑥(cos⁡(𝑥)+sen⁡(𝑥))+𝑒𝑥(−sen⁡(𝑥)+cos⁡(𝑥))=2𝑒𝑥cos⁡(𝑥). Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔2𝑒𝑥cos⁡(𝑥)=0⇔cos⁡(𝑥)=0⇔{𝑥=𝜋2,𝑥=3𝜋2. Estudiamos el signo de la derivada.
    (0,𝜋2) (𝜋2,3𝜋2) (3𝜋2,2𝜋)
    signo de 𝑓′ + − +
    monotonía de 𝑓 → → →
    Así que los puntos (𝜋2,𝑒𝜋2) y (2𝜋,𝑒2𝜋) son máximos relativos y los puntos (0,1) y (3𝜋2,−𝑒𝜋2) son mínimos relativos. Por tanto, (2𝜋,𝑒2𝜋) es el máximo absoluto y (3𝜋2,−𝑒𝜋2) es el mínimo absoluto.
  2. La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =3𝜋2 es 𝑦−𝑓(3𝜋2)=𝑓′(3𝜋2)(𝑥−3𝜋2)⇔𝑦=−𝑒3𝜋2. Observamos que la recta tangente es horizontal, así que la recta normal tiene que ser vertical. Por tanto, su ecuación es 𝑥=3𝜋2.

Ejercicio 3

Considera la función 𝑓 :ℝ →ℝ definida por 𝑓(𝑥) =𝑥3 −𝑥. Calcula el área total de los recintos limitados por la gráfica de la función 𝑓 y la recta normal a dicha gráfica en el punto de abscisa 𝑥 =0.

Resolución

En primer lugar, hallamos la recta normal a la gráfica de 𝑓 en 𝑥 =0. Calculamos la derivada de la función. 𝑓′(𝑥)=3𝑥2−1. La pendiente de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0 es 𝑚𝑡 =𝑓′(0) = −1. Como la recta normal es perpendicular a la recta tangente, su pendiente 𝑚𝑛 ha de verificar 𝑚𝑡⋅𝑚𝑛=−1⇔𝑚𝑛=−1𝑚𝑡𝑚𝑡=−1←←←←←←←←←→𝑚𝑛=1. Así que la recta normal a la gráfica de 𝑓 en 𝑥 =0 se puede hallar usando la ecuación punto-pendiente como 𝑦−𝑓(0)=𝑚𝑛(𝑥−0)⇔𝑦=𝑥.

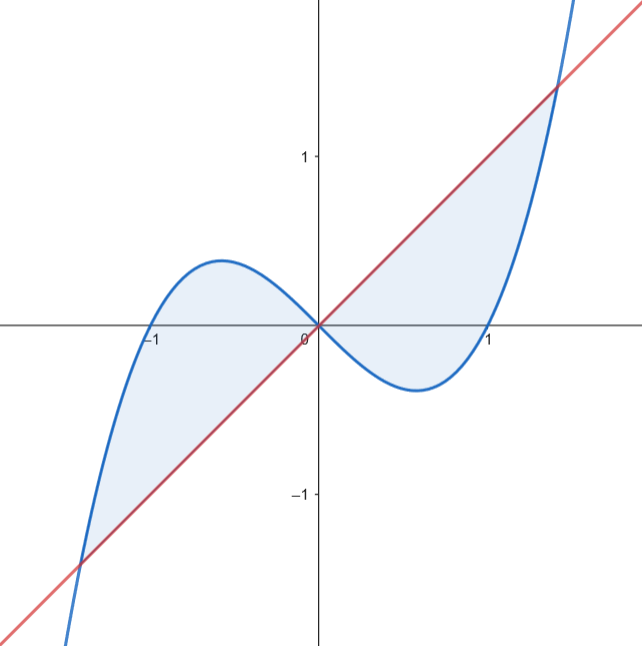
Calculamos los puntos de corte de la función con la recta. 𝑓(𝑥)=𝑥⇔𝑥3−𝑥=𝑥⇔𝑥3−2𝑥=0⇔𝑥(𝑥2−2)=0⇔{𝑥=0,𝑥2−2=0⇔𝑥2=2⇔𝑥=±√2. Podemos representar el recinto limitado por la gráfica de 𝑓 y la recta 𝑦 =𝑥. Figura

Como los dos recintos tienen la misma superficie, podemos calcular el área como 2∫√20(𝑥−(𝑥3−𝑥))𝑑𝑥=2∫√20(2𝑥−𝑥3)𝑑𝑥=2[𝑥2−14𝑥4]√20=2(2−1)=2𝑢2.

Ejercicio 4

Calcula ∫30𝑥√1+𝑥𝑑𝑥. (Sugerencia: efectúa el cambio de variable 𝑡 =√1+𝑥).

Resolución

En primer lugar, hallamos una primitiva de la función 𝑓(𝑥)=𝑥√1+𝑥.

Para resolver esta integral, usamos el cambio de variable 𝑡=√1+𝑥⇒𝑡2=1+𝑥⇒𝑥=𝑡2−1,𝑑𝑥=2𝑡𝑑𝑡. De esta forma, ∫𝑥√1+𝑥𝑑𝑥=∫𝑡2−1𝑡2𝑡𝑑𝑡=2∫(𝑡2−1)𝑑𝑡=23𝑡3−2𝑡=23(1+𝑥)3/2−2√1+𝑥=23(𝑥−2)√1+𝑥.

Por último, calculamos la integral definida. ∫30𝑥√1+𝑥𝑑𝑥=23[(𝑥−2)√1+𝑥]30=23(2+2)=83.

Ejercicio 5

La suma de los seguidores en una determinada red social de Alberto, Begoña y Carlos es de 13000 personas. Aunque Carlos perdiera una tercera parte de sus seguidores, todavía seguiría teniendo el doble de seguidores que tiene Alberto. Por otro lado, los seguidores de Alberto más la quinta parte de los seguidores de Begoña, son tantos como la mitad de los de Carlos. Calcula cuántos seguidores tienen cada uno.

Resolución

Llamamos 𝑥 al número de seguidores de Alberto, 𝑦 al de Begoña y 𝑧 al de Carlos.

En primer lugar, si entre los tres tienen 13000, entonces 𝑥+𝑦+𝑧=13000.

Además, si dos terceras partes de los seguidores de Carlos son tantos como el doble de los de Alberto, 23𝑧=2𝑥.

Por último, si los seguidores de Alberto junto con la quinta parte de los de Begoña son tantos como la mitad de los de Carlos, 𝑥+15𝑦=12𝑧.

Por tanto, podemos plantear el sistema de ecuaciones lineales ⎧{ {⎨{ {⎩𝑥+𝑦+𝑧=13000,23𝑧=2𝑥,𝑥+15𝑦=12𝑧⇒⎧{ {⎨{ {⎩𝑥+𝑦+𝑧=13000,3𝑥−𝑧=0,10𝑥+2𝑦−5𝑧=0.

Resolvemos el sistema mediante el método de Gauss. ⎛⎜ ⎜ ⎜ ⎜⎝1111300030−10102−50⎞⎟ ⎟ ⎟ ⎟⎠𝐹3−2𝐹1←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜⎝1111300030−1080−7−26000⎞⎟ ⎟ ⎟ ⎟⎠𝐹3−7𝐹2←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜⎝1111300030−10−1300−26000⎞⎟ ⎟ ⎟ ⎟⎠ El sistema resultante es ⎧{ {⎨{ {⎩𝑥+𝑦+𝑧=13000,3𝑥−𝑧=0,−13𝑥=−26000.

Por tanto, −13𝑥=−26000⇔𝑥=2000,3𝑥−𝑧=0𝑥=2000←←←←←←←←←→6000−𝑧=0⇔𝑧=6000,𝑥+𝑦+𝑧=13000𝑥=2000←←←←←←←←←→𝑧=60002000+𝑦+6000=13000⇔𝑦=5000. Así que Alberto tiene 2000 seguidores, Begoña tiene 5000 y Carlos tiene 6000.

Ejercicio 6

Considera las matrices 𝐴=⎛⎜ ⎜ ⎜⎝𝑚131𝑚21𝑚3⎞⎟ ⎟ ⎟⎠y𝐵=⎛⎜ ⎜ ⎜⎝2210−12⎞⎟ ⎟ ⎟⎠.

  1. Calcula el rango de la matriz 𝐴 según los valores de 𝑚.
  2. Para 𝑚 =0 resuelve la ecuación 𝐴𝑋 =𝐵, si es posible.

Resolución
  1. En primer lugar, calculamos el determinante de la matriz 𝐴. |𝐴|=∣𝑚131𝑚21𝑚3∣=3𝑚2+2+3𝑚−3𝑚−3−2𝑚2=𝑚2−1. Observamos que |𝐴|=0⇔𝑚2−1=0⇔𝑚2=1⇔𝑚=±1. Así que, si 𝑚 ≠ ±1, entonces rang⁡(𝐴) =3. En caso contrario, rang⁡(𝐴) ≤2. Estudiamos estos casos.
    • Si 𝑚 = −1, 𝐴=⎛⎜ ⎜ ⎜⎝−1131−121−13⎞⎟ ⎟ ⎟⎠. Como ∣13−12∣=5≠0, entonces rang⁡(𝐴) =2.
    • Si 𝑚 = −1, 𝐴=⎛⎜ ⎜ ⎜⎝113112113⎞⎟ ⎟ ⎟⎠. Como ∣1312∣=−1≠0, entonces rang⁡(𝐴) =2.
    Por tanto,
    • Si 𝑚 ≠ ±1, entonces rang⁡(𝐴) =3.
    • Si 𝑚 = −1 o 𝑚 =1, entonces rang⁡(𝐴) =2.
  2. Resolvemos la ecuación matricial para 𝑚 =0. 𝐴𝑋=𝐵⇔𝑋=𝐴−1𝐵. Como 𝑚 =0, por el apartado anterior 𝐴 es invertible y det(𝐴) = −1. Para hallar la inversa de la matriz 𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐴)=⎛⎜ ⎜ ⎜⎝0−10−3−3123−1⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como 𝐴−1=1|𝐴|Adj⁡(𝐴)𝑡=−⎛⎜ ⎜ ⎜⎝0−32−1−3301−1⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝03−213−30−11⎞⎟ ⎟ ⎟⎠. Por último, calculamos la matriz 𝑋 operando. 𝑋=𝐴−1𝐵=⎛⎜ ⎜ ⎜⎝03−213−30−11⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝2210−12⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝5−48−4−22⎞⎟ ⎟ ⎟⎠.

Ejercicio 7

Considera el triángulo cuyos vértices son los puntos 𝐴(0,2,3), 𝐵(𝑚,0,1) y 𝐶(2,1,2).

  1. Halla los valores de 𝑚, sabiendo que el área del triángulo es √182 unidades cuadradas.
  2. Para 𝑚 =0, calcula el coseno del ángulo en el vértice 𝐴 de dicho triángulo.

Resolución
  1. El área del triángulo formado por 𝐴, 𝐵 y 𝐶 es la mitad del área del paralelogramo determinado por dichos puntos, es decir, el paralelogramo formado por los vectores ⃗𝐴𝐵 =(𝑚, −2, −2) y ⃗𝐴𝐶 =(2, −1, −1). Esta viene dada por el módulo del producto vectorial de los vectores. ⃗𝐴𝐵×⃗𝐴𝐶=∣⃗𝑥⃗𝑦⃗𝑧𝑚−2−22−1−1∣=(0,𝑚−4,−𝑚+4). Así que el área del triángulo es |⃗𝐴𝐵×⃗𝐴𝐶|2=|(0,𝑚−4,−𝑚+4)|2=√(𝑚−4)2+(−𝑚+4)22=√2𝑚2−16𝑚+322. Si el área es de √182 𝑢2, entonces √2𝑚2−16𝑚+322=√182⇔2𝑚2−16𝑚+32=18⇔𝑚2−8𝑚+7=0⇔{𝑚=1,𝑚=7. Por tanto, los posibles valores son 𝑚 =1 y 𝑚 =7.
  2. El ángulo en el vértice 𝐴 viene dado por el ángulo 𝛼 que forman los vectores ⃗𝐴𝐵 =(0, −2, −2) y ⃗𝐴𝐶 =(2, −1, −1). Por tanto, cos⁡(𝛼)=⃗𝐴𝐵⋅⃗𝐴𝐶|⃗𝐴𝐵||⃗𝐴𝐶|=4√8√6=1√3.

Ejercicio 8

Considera el punto 𝑃(2,0, −4) y el plano 𝜋≡⎧{ {⎨{ {⎩𝑥=9𝛼+3𝛽,𝑦=−1+2𝛼,𝑧=3+4𝛼+𝛽.

  1. Halla el punto simétrico del punto 𝑃 respecto del plano 𝜋.
  2. Calcula la distancia del punto 𝑃 al plano 𝜋.

Resolución
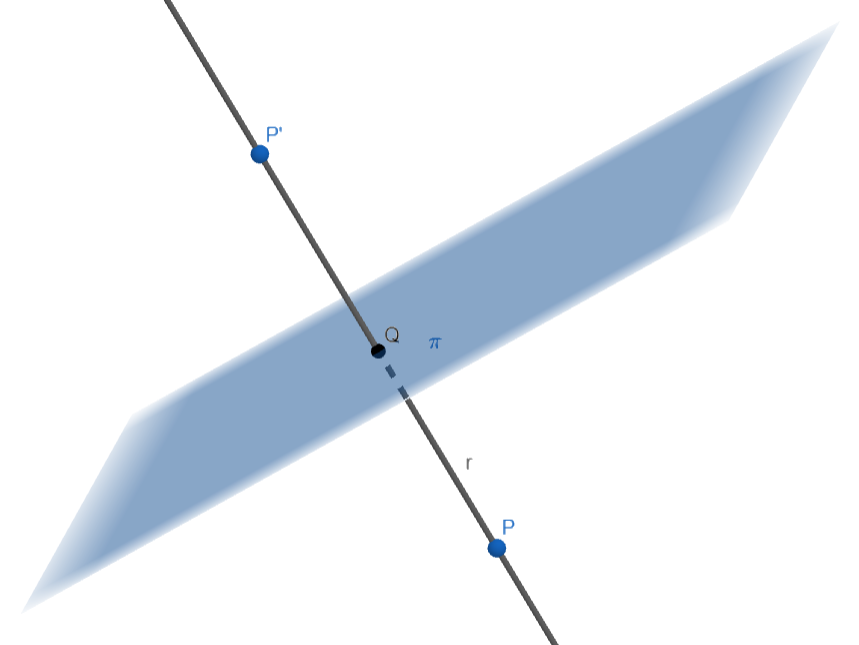  1. En primer lugar, hallamos la ecuación general del plano 𝜋. Su vector normal viene dado por el producto vectorial ⃗𝑛=(9,2,4)×(3,0,1)=∣⃗𝑥⃗𝑦⃗𝑧924301∣=(2,3,−6). Como el punto (0, −1,3) pertenece al plano 𝜋, su ecuación general es 𝜋≡2𝑥+3(𝑦+1)−6(𝑦−3)=0⇔2𝑥+3𝑦−6𝑧+21=0. Para hallar el punto simétrico 𝑃′ de 𝑃 con respecto a 𝜋, trazamos una recta 𝑟 perpendicular al plano que pase por el punto 𝑃. Figura Al ser perpendicular a 𝜋, el vector director de la recta es ⃗𝑛 =(2,3, −6). Así que la ecuación de la recta 𝑟 es 𝑟≡⎧{ {⎨{ {⎩𝑥=2+2𝜆,𝑦=3𝜆,𝑧=−4−6𝜆. A continuación, hallamos el punto de intersección 𝑄 de la recta y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 2(2+𝜆)+3⋅3𝜆−6(−4−6𝜆)+21=0⇔49𝜆+49=0⇔𝜆=−1. Por tanto, el punto de corte es 𝑄(0, −3,2). Como 𝑄 es el punto medio de 𝑃 y 𝑃′, podemos hallar 𝑃′ como el simétrico de 𝑃 con respecto a 𝑄. Si llamamos 𝑃′(𝑎,𝑏,𝑐), tiene que verificarse ⎧{ {⎨{ {⎩2+𝑎2=0⇔𝑎=−2,0+𝑏2=−3⇔𝑏=−6,−4+𝑐2=2⇔𝑐=8. Por tanto, el punto simétrico de 𝑃 con respecto al plano 𝜋 es 𝑃′( −2, −6,8).
  2. Por el apartado anterior, dist⁡(𝑃,𝜋) =dist⁡(𝑃,𝑄). Calculamos la distancia de 𝑃 a 𝜋 como el módulo del vector ⃗𝑃𝑄 =( −2, −3,6). dist⁡(𝑃,𝜋)=dist⁡(𝑃,𝑄)=|⃗𝑃𝑄|=√22+32+62=√49=7𝑢.