Ejercicio 2: Reserva 1 de 2025
Sea la función
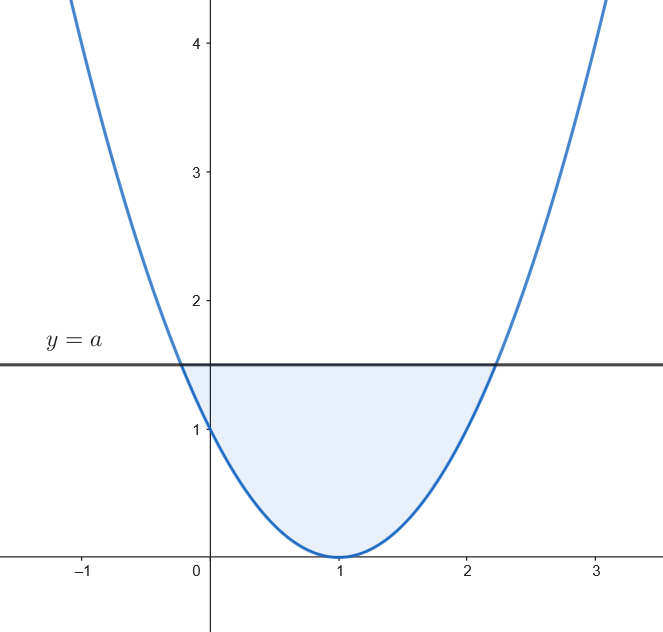
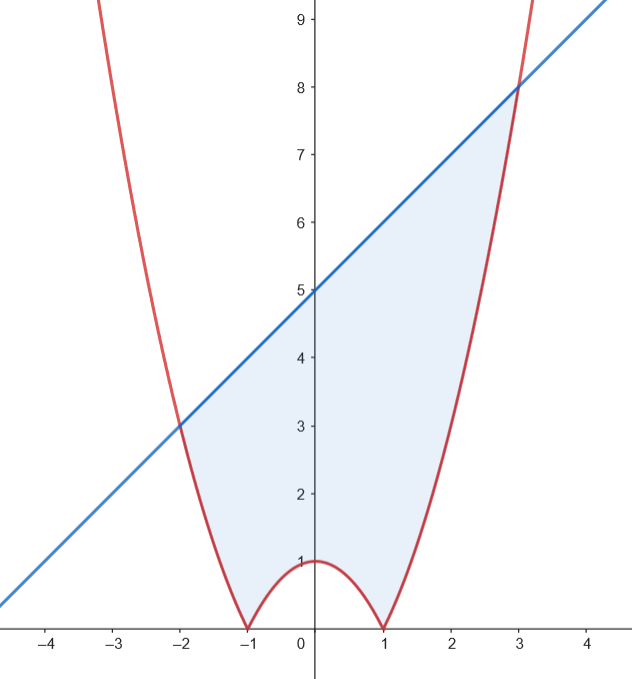
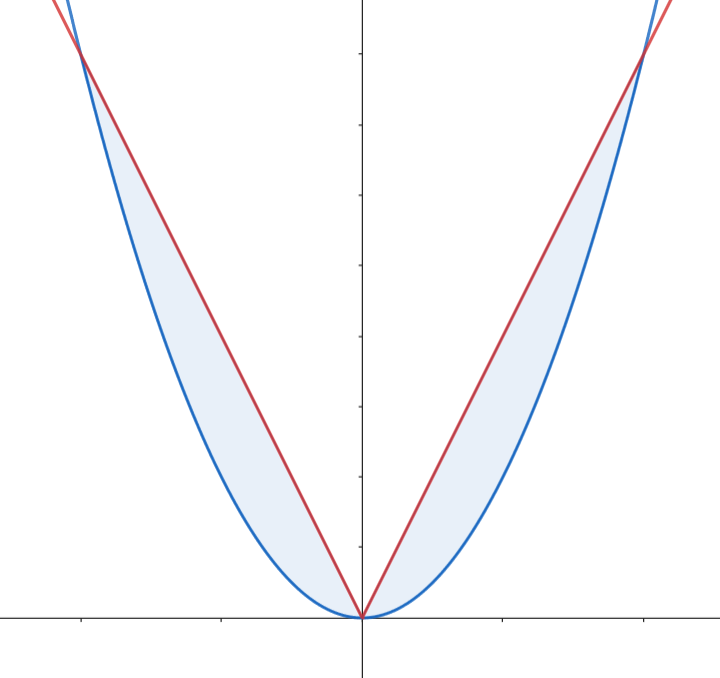
- Esboza el recinto acotado y limitado por la gráfica de
𝑓 𝑦 = 𝑎 𝑎 > 0 - Calcula
𝑎 > 0 𝑓 𝑦 = 𝑎 4 3
Resolución
-
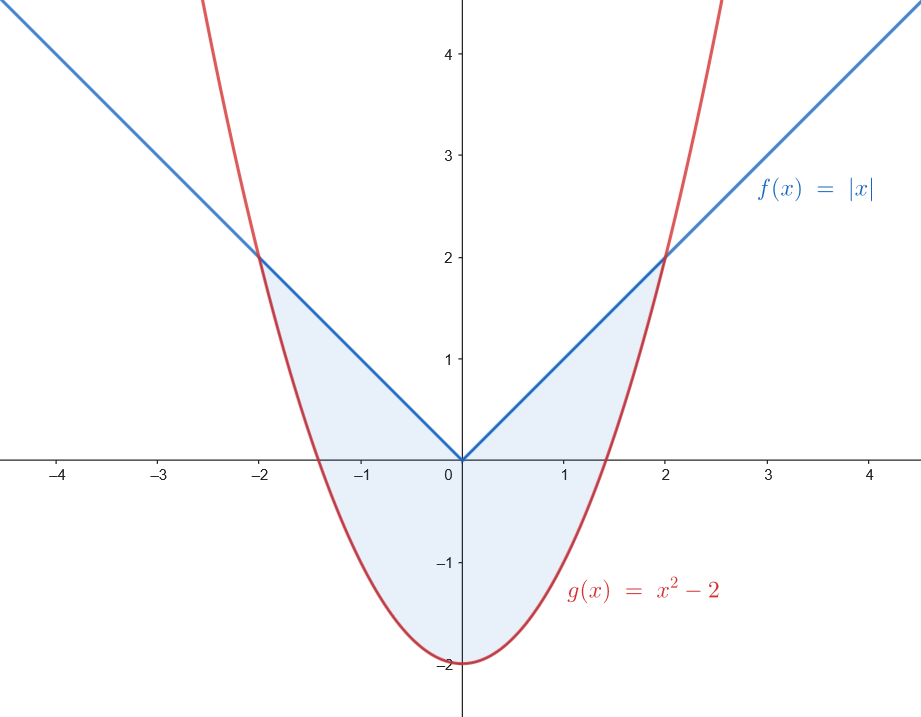
Representamos el recinto.
-
En primer lugar, hallamos los puntos de corte entre la función y la recta.
𝑓 ( 𝑥 ) = 𝑎 ⇔ ( 𝑥 − 1 ) 2 = 𝑎 ⇔ | 𝑥 − 1 | = √ 𝑎 ⇔ { 𝑥 − 1 = √ 𝑎 ⇔ 𝑥 = 1 + √ 𝑎 , 𝑥 − 1 = − √ 𝑎 ⇔ 𝑥 = 1 − √ 𝑎 . 𝑆 = 2 ∫ 1 + √ 𝑎 0 ( 𝑥 2 − 2 𝑥 + 1 ) 𝑑 𝑥 = 2 [ 𝑥 3 3 − 𝑥 2 + 𝑥 ] 1 + √ 𝑎 0 = 2 ( ( 1 + √ 𝑎 ) 3 3 − ( 1 + √ 𝑎 ) 2 + 1 + √ 𝑎 ) . 4 3 𝑆 = 4 3 ⇔ 2 ( ( 1 + √ 𝑎 ) 3 3 − ( 1 + √ 𝑎 ) 2 + 1 + √ 𝑎 ) = 4 3 . 𝑡 = 1 + √ 𝑎 2 ( 𝑡 3 3 − 𝑡 2 + 𝑡 ) = 4 3 ⇔ 𝑡 3 3 − 𝑡 2 + 𝑡 = 2 3 ⇔ 𝑡 3 − 3 𝑡 2 + 3 𝑡 − 2 = 0 ⇔ ( 𝑡 − 2 ) ( 𝑡 2 − 𝑡 + 1 ) = 0 ⇔ 𝑡 = 2 . 1 + √ 𝑎 = 2 ⇔ √ 𝑎 = 1 ⇔ 𝑎 = 1 .
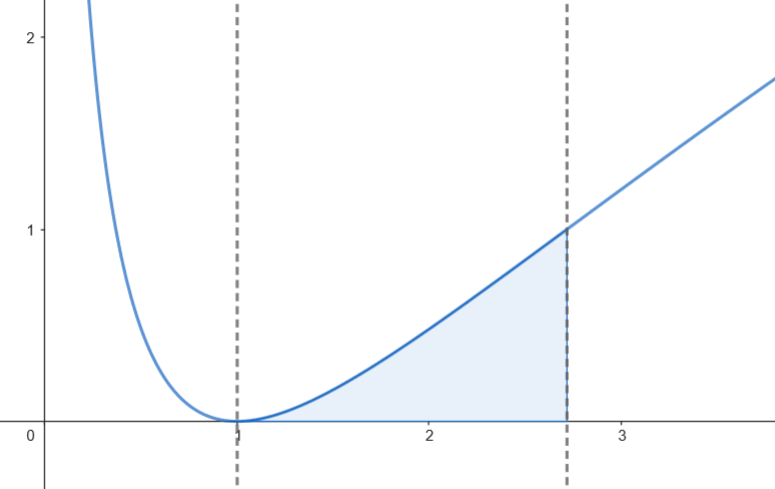
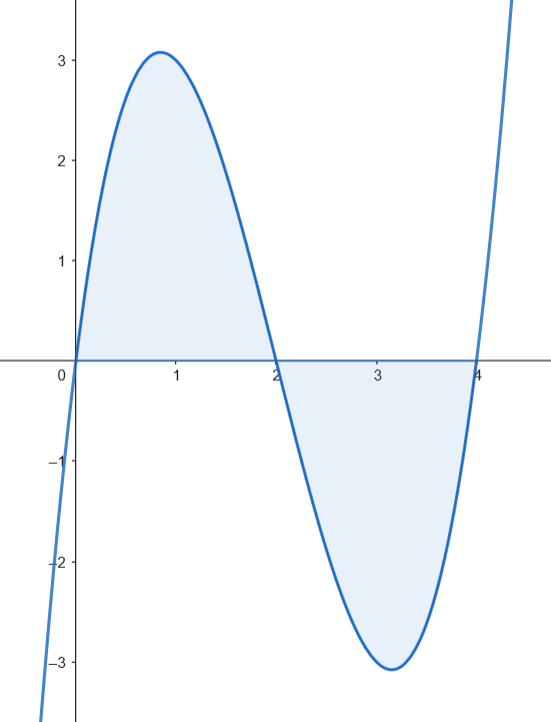 Calculamos el área de los recintos.
Calculamos el área de los recintos.
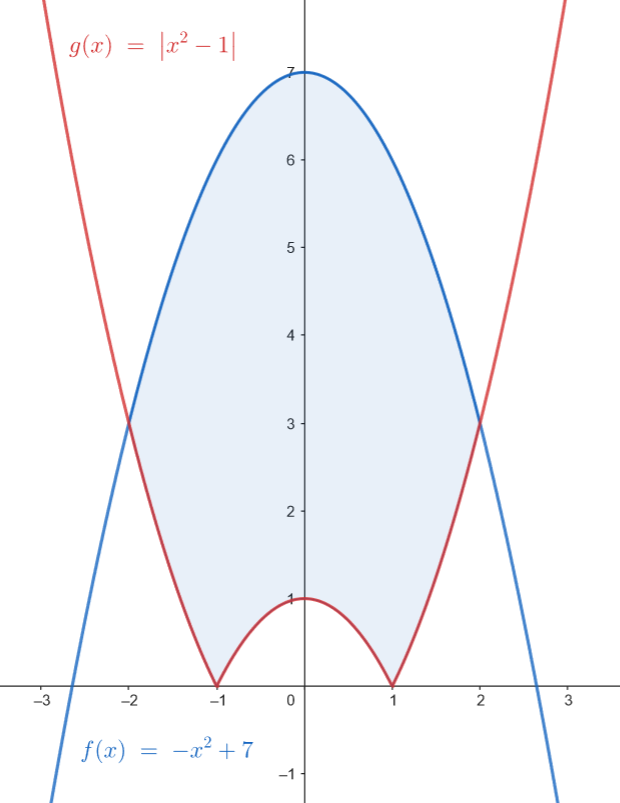
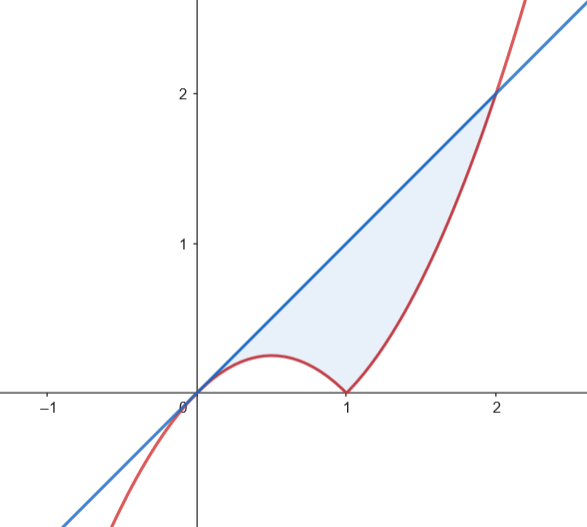
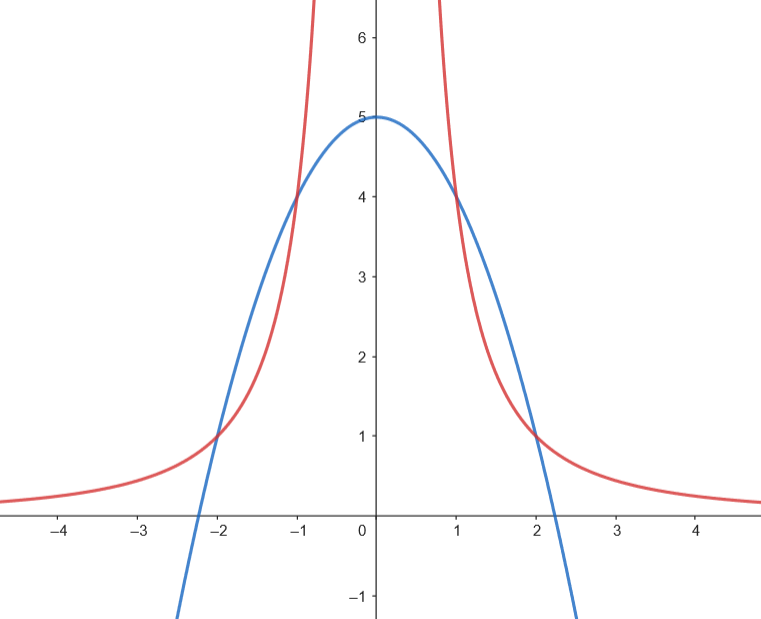
 Calculamos el área del recinto.
Calculamos el área del recinto.
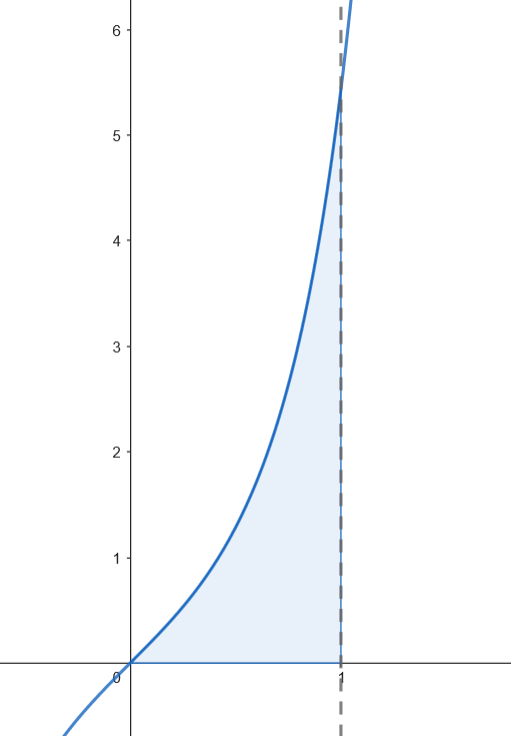 Calculamos el área del recinto.
Calculamos el área del recinto.
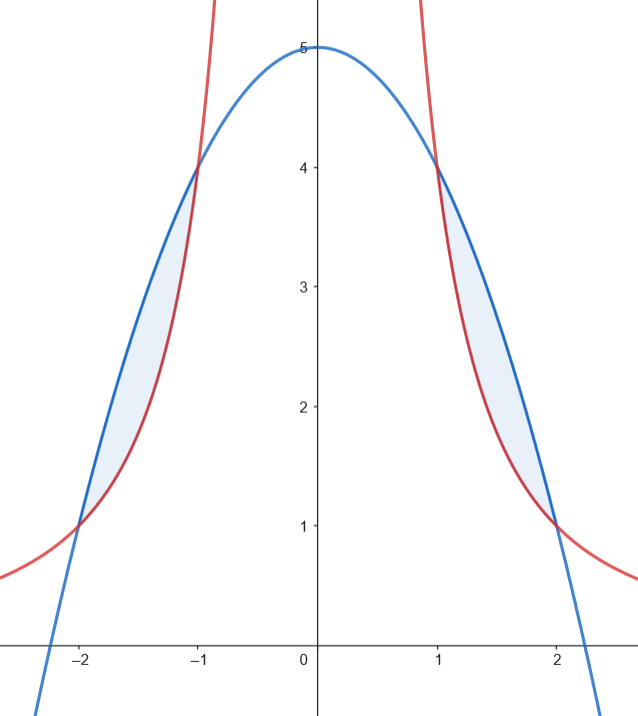 Como los dos recintos tienen la misma superficie, podemos calcular el área como
Como los dos recintos tienen la misma superficie, podemos calcular el área como
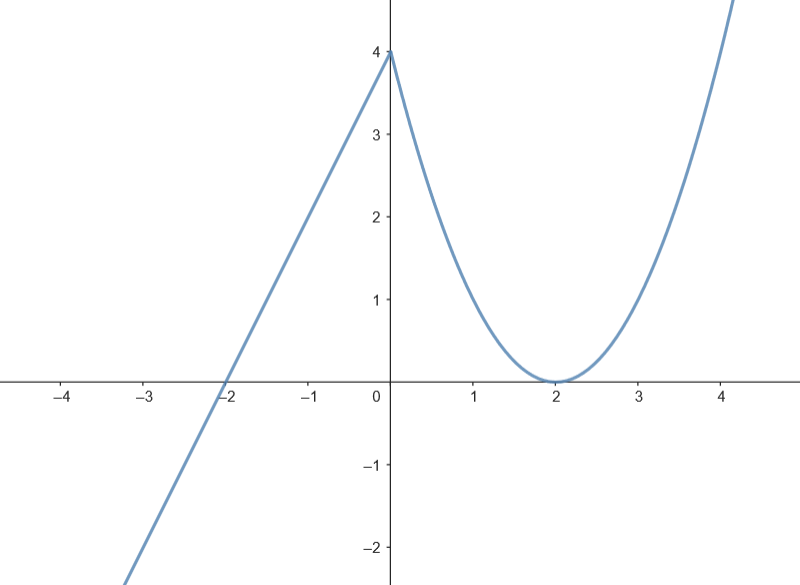
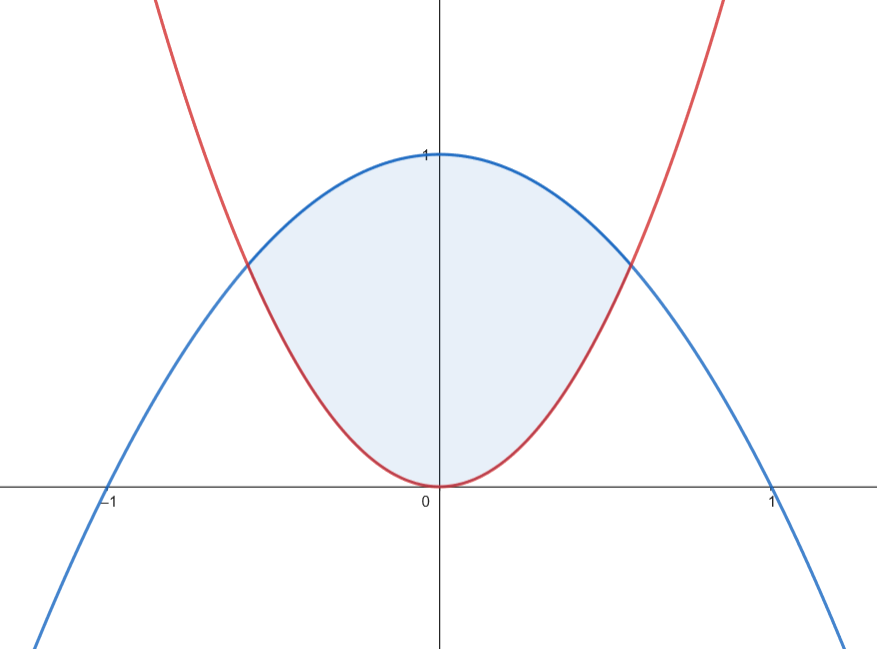
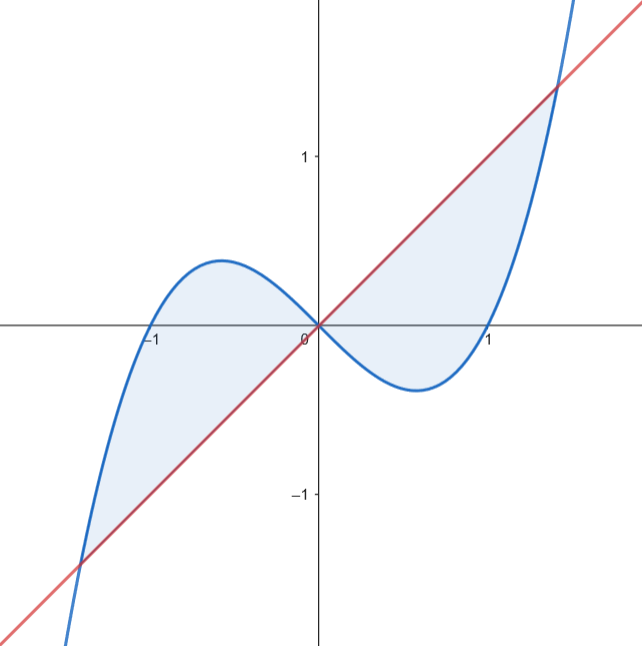
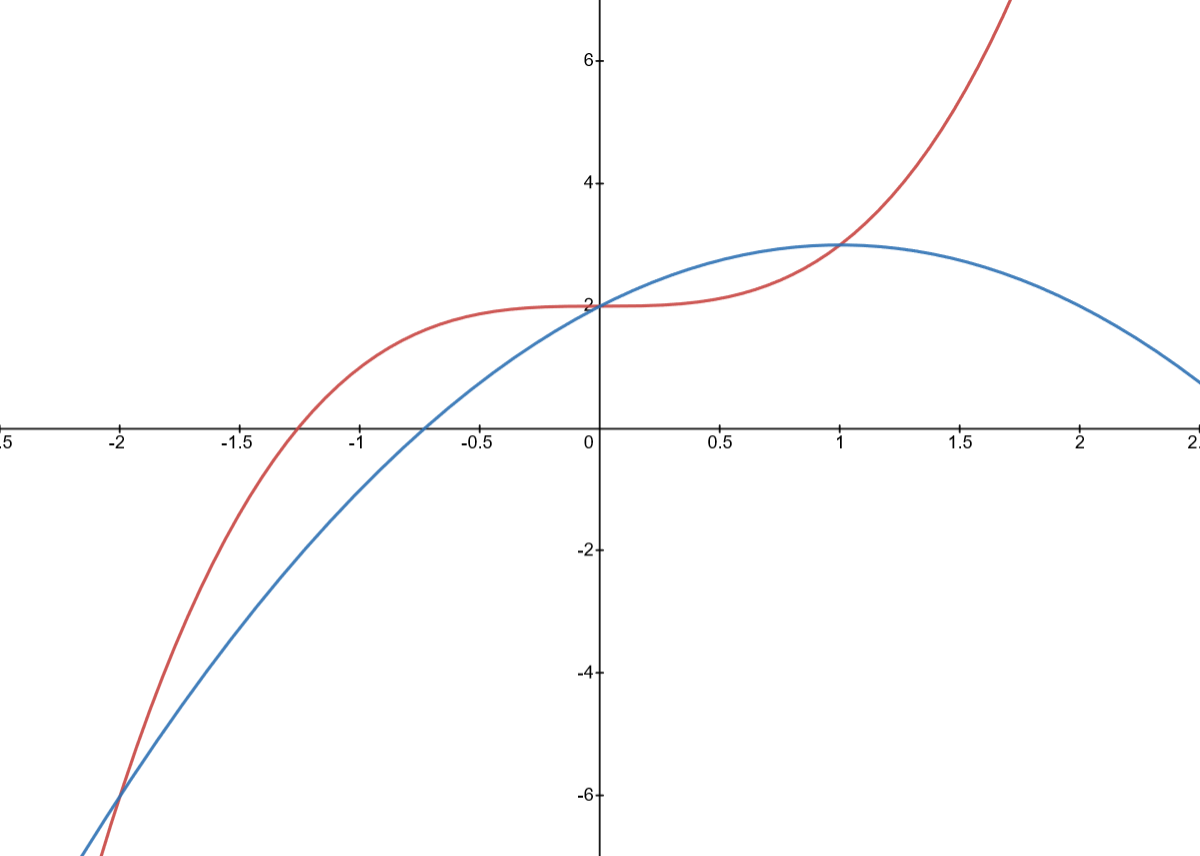
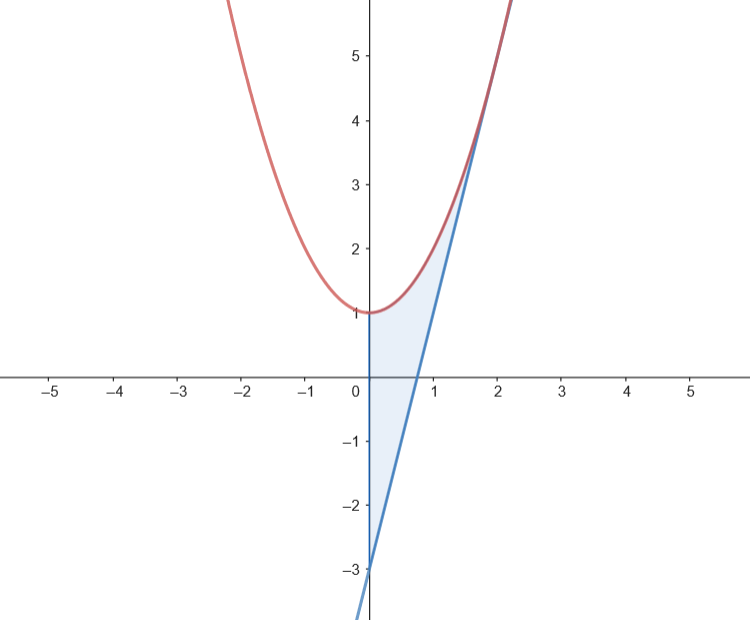
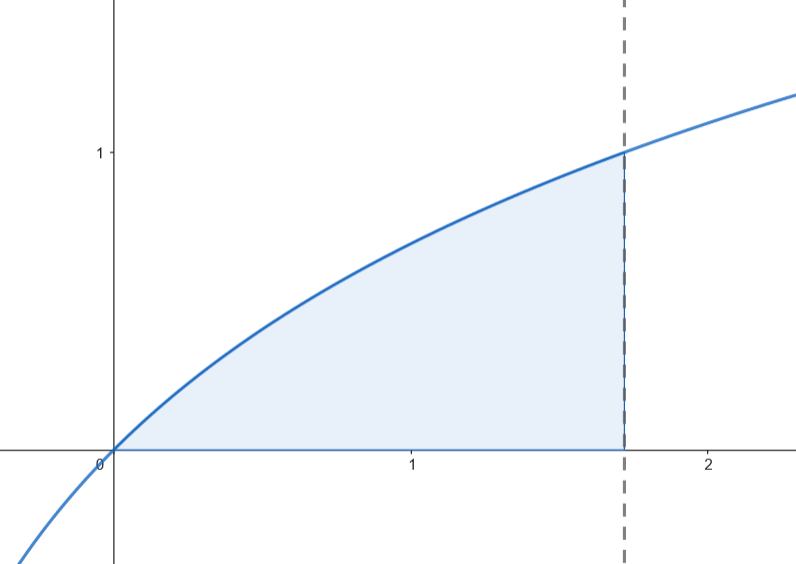
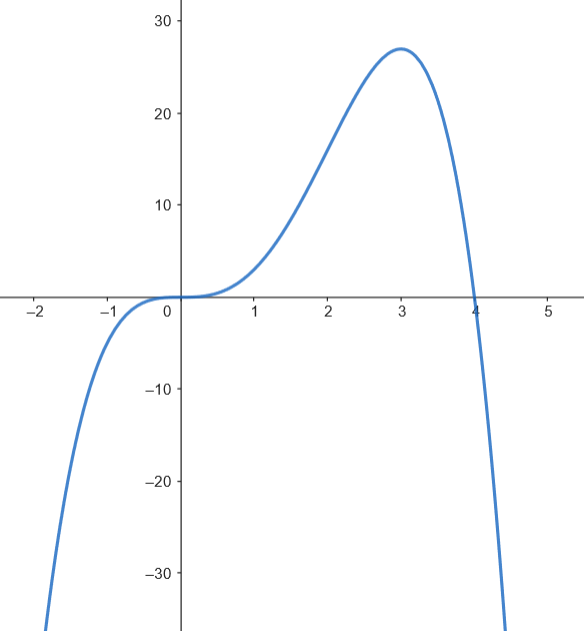 Podemos representar gráficamente el recinto limitado por la gráfica de
Podemos representar gráficamente el recinto limitado por la gráfica de 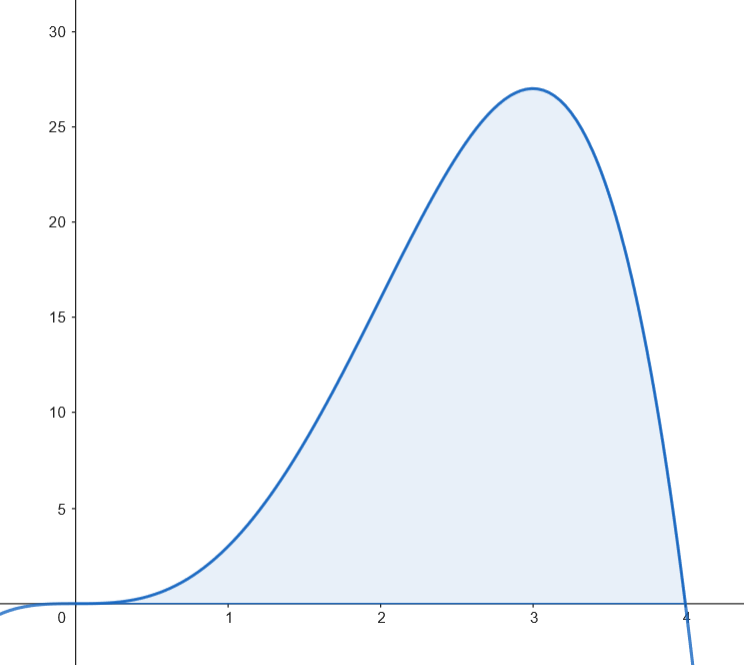 Calculamos el área.
Calculamos el área.
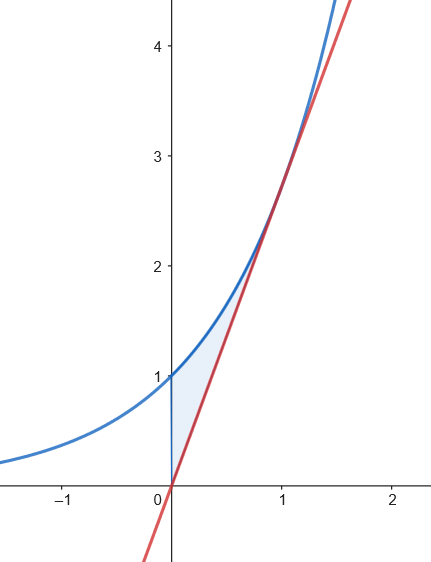 Calculamos el área.
Calculamos el área.
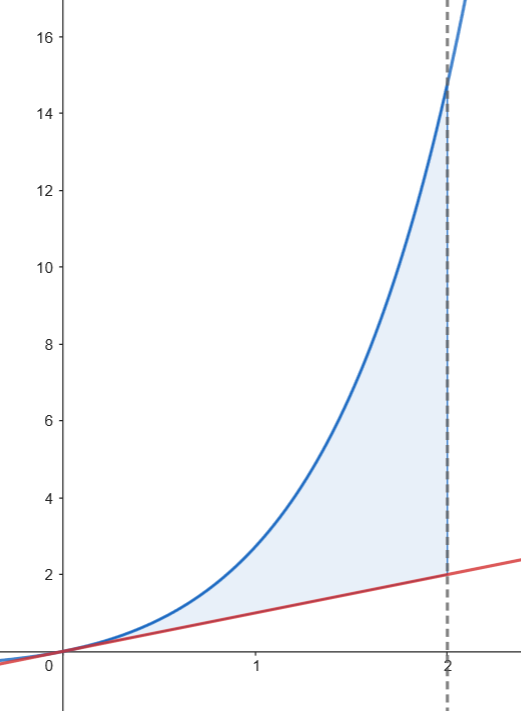
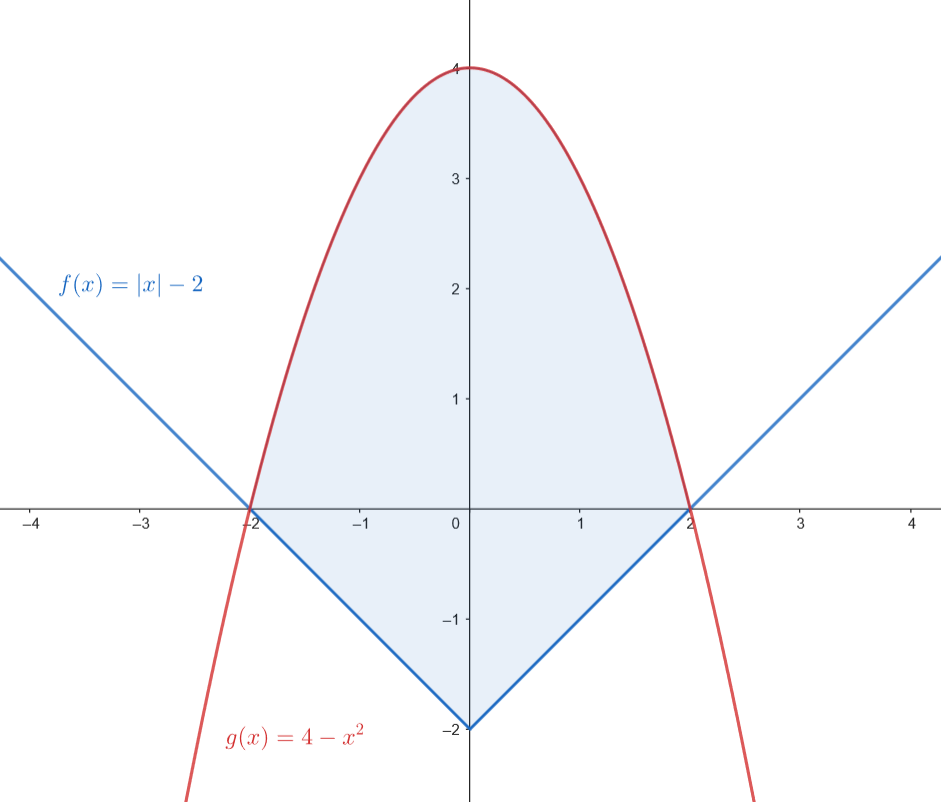
 El área de la región viene dada por
El área de la región viene dada por
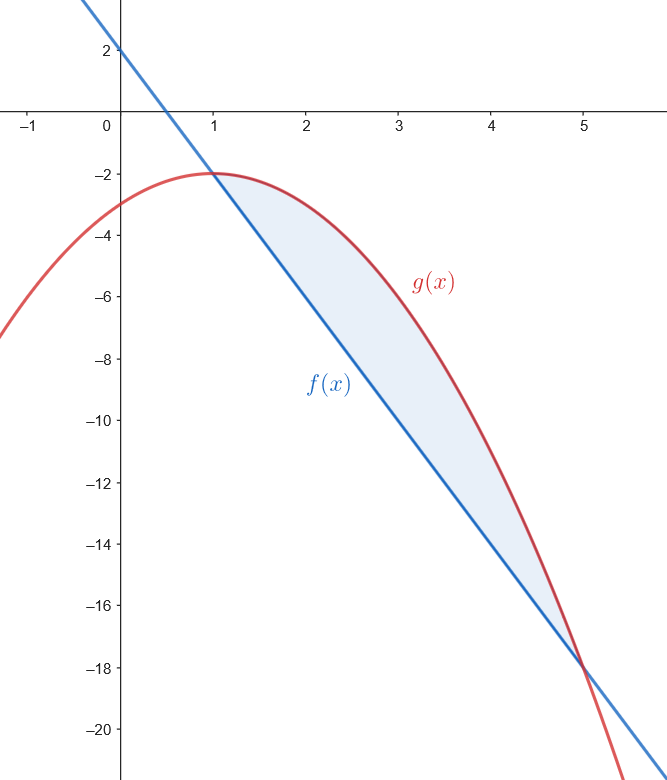 Calculamos el área.
Calculamos el área.