Ejercicio 3: Junio de 2025
Sea la función
- Calcula
𝑎 𝑦 = 1 𝑓 -
Para
𝑎 = 0 𝑓 𝑓
Resolución
-
La ordenada de la asíntota horizontal viene dada por:
l í m 𝑥 → + ∞ 𝑓 ( 𝑥 ) = l í m 𝑥 → + ∞ ( 𝑎 + l n ( 𝑥 ) 𝑥 2 ) = 𝑎 . 𝑦 = 1 𝑎 = 1 -
En primer lugar, hallamos la derivada de la función
𝑓 𝑓 ′ ( 𝑥 ) = 1 𝑥 ⋅ 𝑥 2 − l n ( 𝑥 ) ⋅ 2 𝑥 𝑥 4 = 𝑥 − 2 𝑥 l n ( 𝑥 ) 𝑥 4 = 1 − 2 l n ( 𝑥 ) 𝑥 3 . 𝑓 𝑓 ′ ( 𝑥 ) = 0 ⇔ 1 − 2 l n ( 𝑥 ) 𝑥 3 = 0 ⇔ 1 − 2 l n ( 𝑥 ) = 0 ⇔ l n ( 𝑥 ) = 1 2 ⇔ 𝑥 = √ 𝑒 . Por tanto,( 0 , √ 𝑒 ) ( √ 𝑒 , + ∞ ) signo de 𝑓 ′ + − monotonía de 𝑓 → → 𝑓 ( 0 , √ 𝑒 ) ( √ 𝑒 , + ∞ ) ( √ 𝑒 , 1 2 𝑒 )
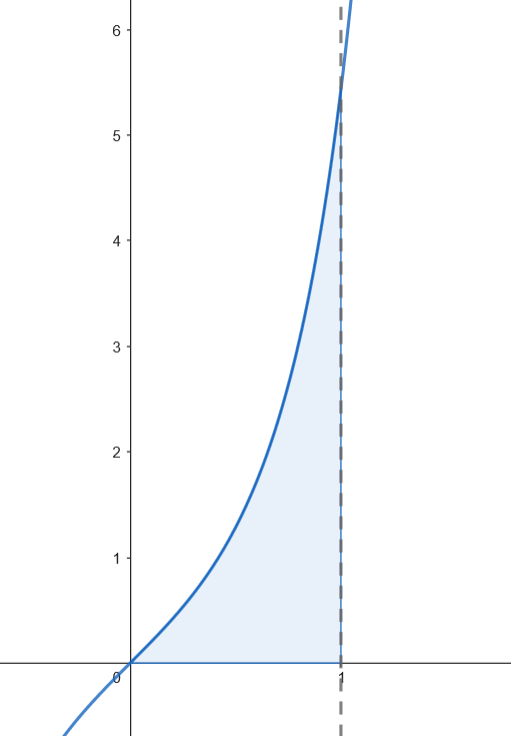 Calculamos el área del recinto.
Calculamos el área del recinto.
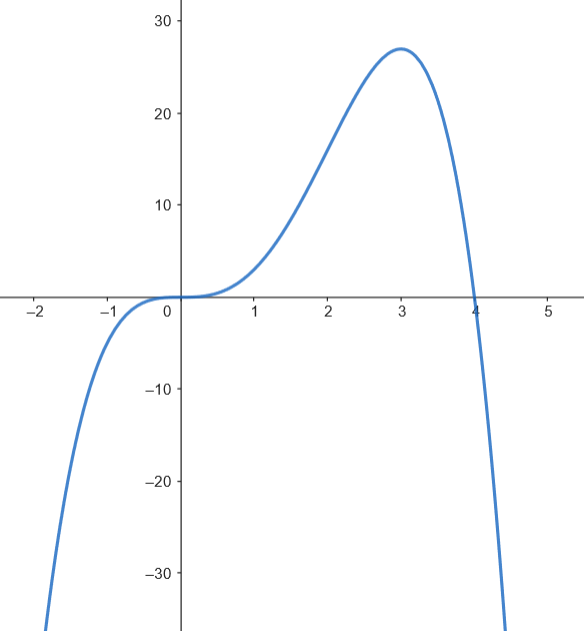 Podemos representar gráficamente el recinto limitado por la gráfica de
Podemos representar gráficamente el recinto limitado por la gráfica de 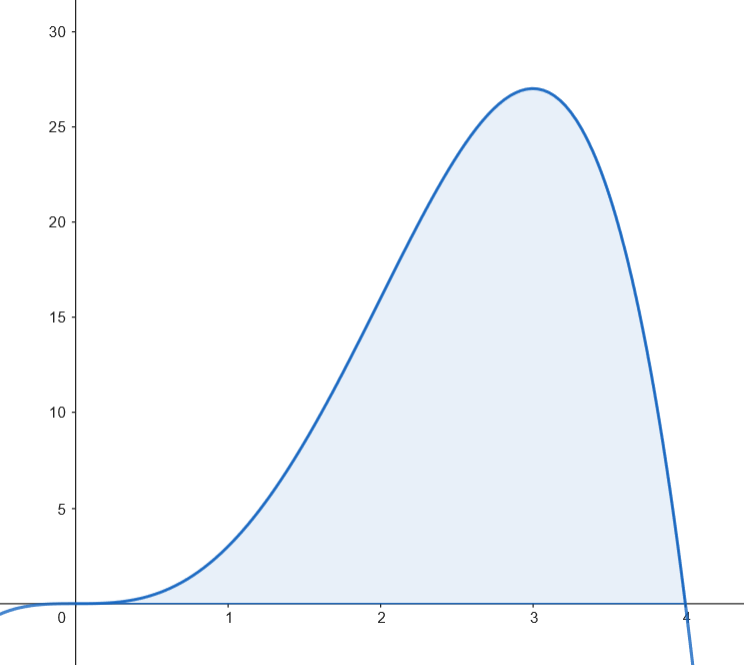 Calculamos el área.
Calculamos el área.
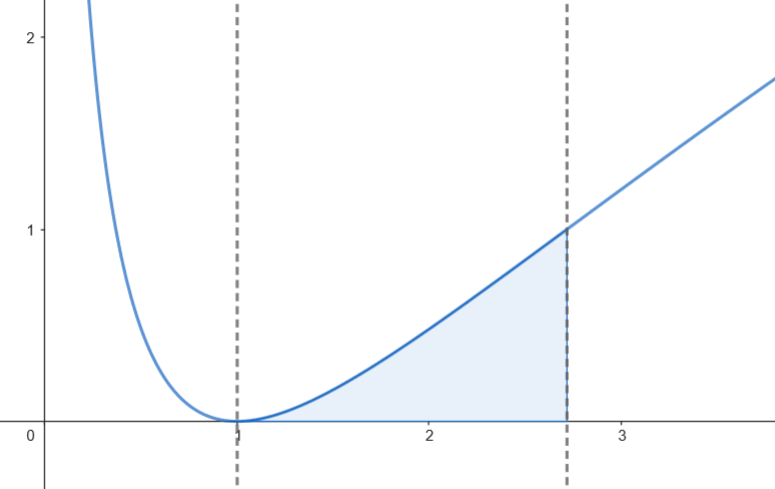 El área de la región viene dada por
El área de la región viene dada por
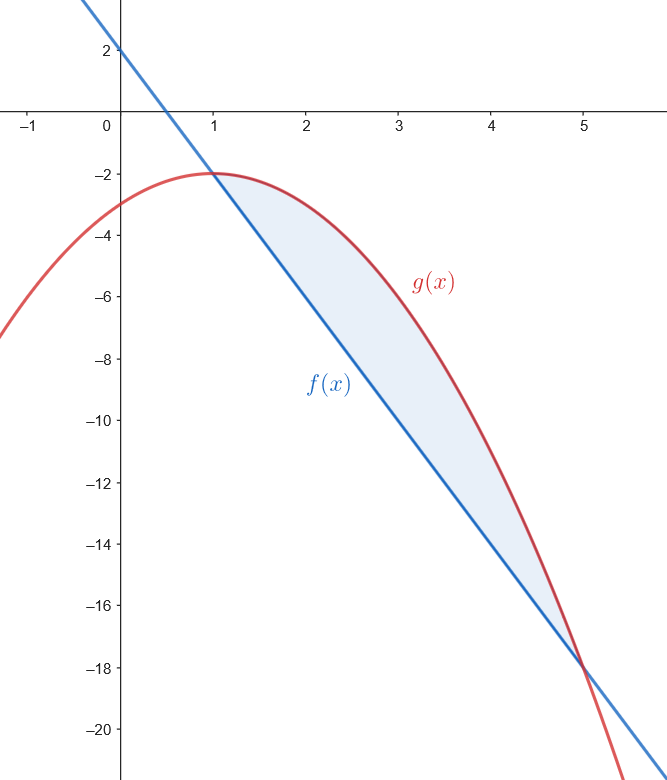 Calculamos el área.
Calculamos el área.