Ejercicio 1
Sabiendo que
Resolución
Calculamos el límite.
Para resolver la indeterminación, aplicamos la regla de l'Hôpital.
Continuamos resolviendo el límite para
Sabiendo que
Calculamos el límite.
Para resolver la indeterminación, aplicamos la regla de l'Hôpital.
Continuamos resolviendo el límite para
Determina la función
Como
De igual forma, como
Considera el sistema de ecuaciones
Considera el punto
En primer lugar, hallamos las ecuaciones paramétricas de la recta
Sea
En primer lugar, escribimos
| signo de |
|||
| monotonía de |
Considera las funciones
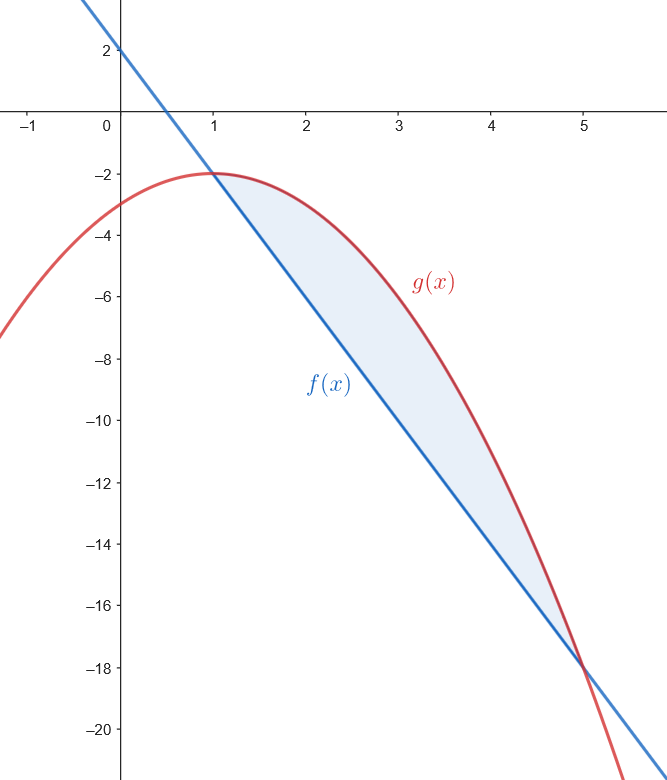 Calculamos el área.
Calculamos el área.
Considera la matriz
Considera los vectores