En primer lugar, hallamos el vector normal del plano $\pi_1.$
Como está determinado por los puntos $A$, $B$ y $C$, tiene como vectores directores $\vec{AB} = (0, 1, -3)$ y $\vec{AC} = (-1, 1, 1).$
El vector normal del plano es perpendicular a ambos, así que:
$$\vec{n}_1 = \vec{AB} \times \vec{AC} = \begin{vproduct}
0 & 1 & -3 \\
-1 & 1 & 1
\end{vproduct} = (4, 3, 1).$$
Llamamos $r$ a la recta que nos piden.
Como $r$ es paralela a $\pi_1$ y $\pi_2$, el vector director de la recta es perpendicular a $\vec{n}_1 = (4, 3, 1)$ y $\vec{n}_2 = (1, -1, 1).$
Así que:
$$\vec{d}_r = \vec{n}_1 \times \vec{n}_2 = \begin{vproduct}
4 & 3 & 1 \\
1 & -1 & 1
\end{vproduct} = (4, -3, -7).$$
Además, el punto $(0, 0, 0)$ pertenece a la recta.
Por tanto, las ecuaciones paramétricas de la recta $r$ son:
$$r \equiv \begin{cases}
x = 4\lambda, \\
y = -3\lambda, \\
z = -7\lambda.
\end{cases}$$
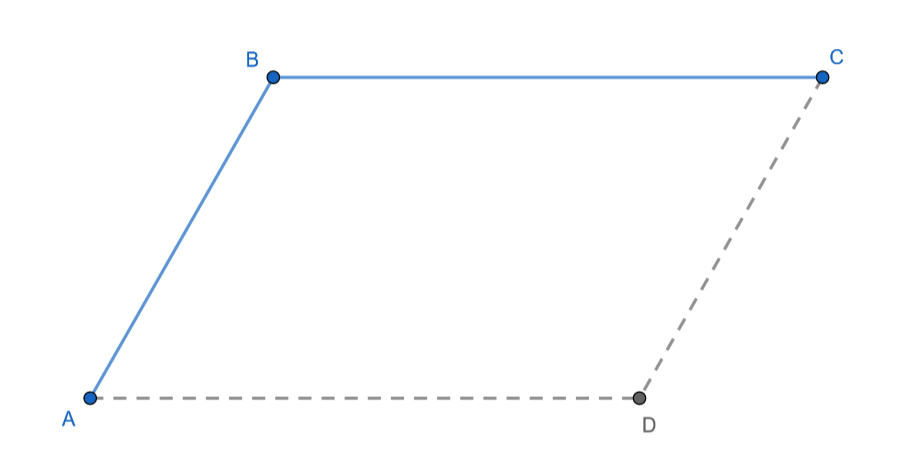 Podemos hallar el punto $D$ trasladando el punto $A$ mediante el vector $\vec{BC} = (0, -1, 1).$
$$\vec{OD} = \vec{OA} + \vec{BC} = (1, 1, 2) + (0, -1, 1) = (1, 0, 3).$$
Por tanto, $D(1, 0, 3).$
Podemos hallar el punto $D$ trasladando el punto $A$ mediante el vector $\vec{BC} = (0, -1, 1).$
$$\vec{OD} = \vec{OA} + \vec{BC} = (1, 1, 2) + (0, -1, 1) = (1, 0, 3).$$
Por tanto, $D(1, 0, 3).$