Matemáticas de Selectividad

1. En primer lugar, hallamos la derivada de la función 𝑓. 𝑓′(𝑥)=2𝑥𝑒𝑥+(𝑥2+1)𝑒𝑥=(𝑥2+2𝑥+1)𝑒𝑥=(𝑥+1)2𝑒𝑥. Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔(𝑥+1)2𝑒𝑥=0⇔(𝑥+1)2=0⇔𝑥+1=0⇔𝑥=−1. Observamos que 𝑓′(𝑥) >0 para valor de 𝑥, así que 𝑓 es creciente en ℝ.
2. En primer lugar, hallamos la segunda derivada de la función 𝑓. 𝑓″(𝑥)=2(𝑥+1)𝑒𝑥+(𝑥+1)2𝑒𝑥=(2𝑥+2)𝑒𝑥+(𝑥2+2𝑥+1)𝑒𝑥=(𝑥2+4𝑥+3)𝑒𝑥. Para hallar los candidatos a puntos de inflexión, igualamos la segunda derivada de 𝑓 a cero. 𝑓″(𝑥)=0⇔(𝑥2+4𝑥+3)𝑒𝑥=0⇔𝑥2+4𝑥+3=0⇔{𝑥=−3,𝑥=−1. Estudiamos el signo de la segunda derivada.

   	( −∞, −3)	( −3, −1)	( −1, +∞)
   signo de 𝑓″	+	−	+
   curvatura de 𝑓	⌣	⌢	⌣

   Por tanto, 𝑓 es convexa en ( −∞, −3) ∪( −1, +∞) y cóncava en ( −3, −1). Además, ( −3,10𝑒−3) y ( −1,2𝑒−1) son los puntos de inflexión.

1. En primer lugar, observamos que 𝑓 es continua y derivable en cada una de sus ramas para cualquier valor de 𝑎 y 𝑏, con 𝑓′(𝑥)=⎧{ { {⎨{ { {⎩−𝑎𝑒−𝑥−𝑏1−𝑥,si 𝑥<0,1+11+𝑥,si 𝑥≥0. Pasamos a estudiar su continuidad y derivabilidad en el punto de ruptura 𝑥 =0.
   • Estudiamos la continuidad. lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0−⁡(𝑎𝑒−𝑥+𝑏ln⁡(1−𝑥))=𝑎,lím𝑥→0+⁡𝑓(𝑥)=lím𝑥→0+⁡(𝑥+ln⁡(1+𝑥))=0,𝑓(0)=0. Como 𝑓 es continua en 𝑥 =0, lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0+⁡𝑓(𝑥)=𝑓(0)⇔𝑎=0.
   • Estudiamos la derivabilidad. 𝑓′−(0)=lím𝑥→0−⁡𝑓′(𝑥)=lím𝑥→0−−𝑏1−𝑥=−𝑏,𝑓′+(0)=lím𝑥→0+⁡𝑓′(𝑥)=lím𝑥→0+⁡1+11+𝑥=2. Como 𝑓 es derivable en 𝑥 =0, 𝑓′−(0)=𝑓′+(0)⇔−𝑏=2⇔𝑏=−2.
   Así que 𝑎 =0 y 𝑏 = −2.
2. • La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =0 es: 𝑦−𝑓(0)=𝑓′(0)(𝑥−0)⇔𝑦=2𝑥.
   • La recta normal a la gráfica de 𝑓 en 𝑥 =0 tiene como pendiente −1𝑓′(0). Por tanto, su ecuación es: 𝑦−𝑓(0)=−1𝑓′(0)(𝑥−0)⇔𝑦=−12𝑥.

1. • Hallamos los puntos de corte de la gráfica de 𝑓 con el eje 𝑋. 𝑓(𝑥)=0⇔𝑥3−6𝑥2+8𝑥=0⇔𝑥(𝑥2−6𝑥+8)=0⇔⎧{ {⎨{ {⎩𝑥=0,𝑥=2,𝑥=4. Por tanto, (0,0), (2,0) y (4,0) son los puntos de corte con el eje de abscisas. Además, (0,0) es también el punto de corte con el eje 𝑌.
   • Para representar correctamente la gráfica de función, estudiamos su monotonía. Hallamos en primer lugar la derivada de la función 𝑓. 𝑓′(𝑥)=3𝑥2−12𝑥+8. Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔3𝑥2−12𝑥+8=0⇔𝑥=2±2√33. Estudiamos el signo de la derivada.

     	(−∞,2−2√33)	(2−2√33,2+2√33)	(2+2√33,+∞)
     signo de 𝑓′	+	−	+
     monotonía de 𝑓	→	→	→

     Por tanto, 𝑓 es creciente en (−∞,2−2√33) ∪(2+2√33,+∞) y decreciente en (2−2√33,2+2√33). Además, el punto (2−2√33,16√39) es un máximo relativo y el punto (2+2√33,−16√39) es un mínimo relativo.
   Representamos gráficamente la función usando esta información.
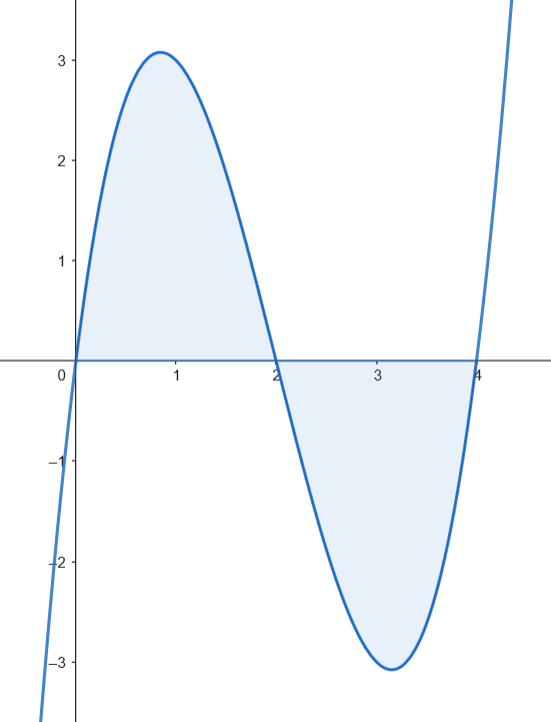2. Podemos representar los recintos limitados por la gráfica de 𝑓 y el eje de abscisas. Calculamos el área de los recintos. ∫20𝑓(𝑥)𝑑𝑥−∫42𝑓(𝑥)𝑑𝑥=∫20(𝑥3−6𝑥2+8𝑥)𝑑𝑥−∫42(𝑥3−6𝑥2+8𝑥)𝑑𝑥==[14𝑥4−2𝑥3+4𝑥2]20−[14𝑥4−2𝑥3+4𝑥2]42=4−16+16−(64−128+64−(4−16+16))=8𝑢2.

Para resolver la integral, usamos el cambio de variable: 𝑡=𝑒𝑥⇒𝑥=ln⁡(𝑡),𝑑𝑥=1𝑡𝑑𝑡. De esta forma, ∫𝑒3𝑥−1𝑒𝑥−3𝑑𝑥=∫𝑡3−1𝑡−3⋅1𝑡𝑑𝑡=∫𝑡3−1𝑡2−3𝑡𝑑𝑡.

Hacemos la división de polinomios del integrando. 𝑡3−1𝑡2−3𝑡=𝑡+3+9𝑡−1𝑡2−3𝑡. Así que: ∫𝑡3−1𝑡2−3𝑡𝑑𝑡=∫(𝑡+3)𝑑𝑡+∫9𝑡−1𝑡2−3𝑡𝑑𝑡=12𝑡2+3𝑡+∫9𝑡−1𝑡2−3𝑡𝑑𝑡.

Expresamos el integrando como suma de fracciones simples. Las raíces del denominador son 0 y 3, así que el integrando se puede escribir como: 9𝑡−1𝑡2−3𝑡=𝐴𝑡+𝐵𝑡−3=𝐴𝑡−3𝐴+𝐵𝑡𝑡2−3𝑡=(𝐴+𝐵)𝑡−3𝐴𝑡2−3𝑡. Igualando ambas expresiones, obtenemos que: {𝐴+𝐵=9,−3𝐴=−1⇔𝐴=13. Despejando y sustituyendo en la primera ecuación, obtenemos que: 𝐴+𝐵=9⇔𝐵=9−𝐴𝐴=1/3←←←←←←←←←←→𝐵=263. Por tanto, 9𝑡−1𝑡2−3𝑡=13𝑡+263(𝑡−3).

Resolvemos la integral. 12𝑡2+3𝑡+∫9𝑡−1𝑡2−3𝑡𝑑𝑡=12𝑡2+3𝑡+13∫1𝑡𝑑𝑡+263∫1𝑡−3𝑑𝑡==12𝑡2+3𝑡+13ln⁡|𝑡|+263ln⁡|𝑡−3|+𝐶=12𝑒2𝑥+3𝑒𝑥+13𝑥+263ln⁡|𝑒𝑥−3|+𝐶.

1. En primer lugar, hallamos los determinantes de las matrices 𝐴 y 𝐵. |𝐴|=∣1−10720001∣=9,|𝐵|=∣ ∣ ∣ ∣2010101900∣ ∣ ∣ ∣=−19.
   • Calculamos el determinante de ((𝐴𝐵)5)−1. |((𝐴𝐵)5)−1|=(|𝐴|⋅|𝐵|)−5=(9⋅(−19))−5=−1.
   • Calculamos el determinante de 27𝐴𝐵6. Como 𝐴 y 𝐵 son de orden 3, |27𝐴𝐵6|=273⋅|𝐴|⋅|𝐵|6=273⋅9⋅(−19)6=13.
2. Por el apartado anterior, 𝐴 y 𝐵 son invertibles. Despejamos la ecuación matricial. 𝐴𝑋𝐵=9𝐼⇔𝑋=9𝐴−1𝐵−1=9(𝐵𝐴)−1. En primer lugar, calculamos 𝐵𝐴. 𝐵𝐴=⎛⎜ ⎜ ⎜ ⎜⎝2010101900⎞⎟ ⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝1−10720001⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜⎝2−2172019−190⎞⎟ ⎟ ⎟ ⎟⎠. Además, su determinante es: |𝐵𝐴|=|𝐵|⋅|𝐴|=−19⋅9=−1. Para hallar la inversa de 𝐵𝐴, calculamos primero su matriz adjunta. Adj⁡(𝐵𝐴)=⎛⎜ ⎜ ⎜ ⎜⎝00−1−19−190−2718⎞⎟ ⎟ ⎟ ⎟⎠. De esta forma, podemos calcular su inversa como: (𝐵𝐴)−1=1|𝐵𝐴|Adj⁡(𝐵𝐴)𝑡=−⎛⎜ ⎜ ⎜ ⎜⎝0−19−20−197−1018⎞⎟ ⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜⎝0192019−710−18⎞⎟ ⎟ ⎟ ⎟⎠. Por tanto, 𝑋=9(𝐵𝐴)−1=9⎛⎜ ⎜ ⎜ ⎜⎝0192019−710−18⎞⎟ ⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝011801−6390−162⎞⎟ ⎟ ⎟⎠.

1. En primer lugar, calculamos el determinante de la matriz 𝐴. |𝐴|=∣10120𝑎53𝑎−10∣=2(3𝑎−1)−𝑎(3𝑎−1)=(2−𝑎)(3𝑎−1). Observamos que: |𝐴|=0⇔(2−𝑎)(3𝑎−1)=0⇔{2−𝑎=0⇔𝑎=2,3𝑎−1=0⇔𝑎=13. Así que rang⁡(𝐴) =3 si 𝑎 ≠13 y 𝑎 ≠2. En caso contrario, rang⁡(𝐴) ≤2. Estudiamos estos casos.
   • Si 𝑎 =13, 𝐴=⎛⎜ ⎜ ⎜ ⎜⎝1012013500⎞⎟ ⎟ ⎟ ⎟⎠. Observamos que: ∣11213∣=−53≠0⇒rang⁡(𝐴)=2.
   • Si 𝑎 =2, 𝐴=⎛⎜ ⎜ ⎜⎝101202550⎞⎟ ⎟ ⎟⎠. Observamos que: ∣1055∣=5≠0⇒rang⁡(𝐴)=2.
   Por tanto,
   • Si 𝑎 ≠13 y 𝑎 ≠2, entonces rang⁡(𝐴) =3.
   • Si 𝑎 =13 o 𝑎 =2, entonces rang⁡(𝐴) =2.
2. Si 𝑎 =2, por el apartado anterior rang⁡(𝐴) =2. La matriz de coeficientes ampliada es: 𝐴∗=⎛⎜ ⎜ ⎜ ⎜⎝101120225504⎞⎟ ⎟ ⎟ ⎟⎠ Observamos que la segunda fila es el doble de la primera, así que rang⁡(𝐴∗) =2. Como rang⁡(𝐴) =rang⁡(𝐴∗) <3, el sistema es compatible determinado. Podemos reducir el sistema a: {𝑥+𝑧=1,5𝑥+5𝑦=4. Si tomamos 𝑥 =𝜆, entonces: 𝑥+𝑧=1⇔𝑧=1−𝑥𝑥=𝜆←←←←←←←→𝑧=1−𝜆,5𝑥+5𝑦=4⇔5𝑦=4−5𝑥⇔𝑦=4−5𝑥5=45−𝑥𝑥=𝜆←←←←←←←→𝑦=45−𝜆. Por tanto, las soluciones del sistema son de la forma: ⎧{ {⎨{ {⎩𝑥=𝜆,𝑦=45−𝜆,𝑧=1−𝜆.

1. Para hallar el punto de 𝑟 a menor distancia de 𝑃, trazamos un plano 𝜋 perpendicular a 𝑟 que pase por 𝑃. Al ser perpendicular a la recta 𝑟, su vector normal es ⃗𝑛𝜋 =⃗𝑑𝑟 =(2,2, −1). Así que la ecuación del plano 𝜋 es: 𝜋≡2𝑥+2(𝑦−2)−(𝑧+4)=0⇔2𝑥+2𝑦−𝑧−8=0. A continuación, calculamos el punto de intersección 𝑄 de la recta y el plano, que será el punto de 𝑟 a menor distancia del punto 𝑃. En primer lugar, hallamos las ecuaciones paramétricas de la recta 𝑟. 𝑟≡⎧{ {⎨{ {⎩𝑥=−1+2𝜆,𝑦=2+2𝜆,𝑧=3−𝜆. Para ello hallar el punto de corte, sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 2(−1+2𝜆)+2(2+2𝜆−2)−(3−𝜆)−8=0⇔9𝜆−9=0⇔𝜆=1. Por tanto, el punto de intersección es 𝑄(1,4,2). Así que este es el punto de 𝑟 a menor distancia de 𝑃.
2. Consideramos un punto genérico 𝑅( −1 +2𝜆,2 +2𝜆,3 −𝜆) de la recta 𝑟. La distancia entre 𝑃 y el punto genérico 𝑅 viene dada por el módulo del vector ⃗𝑃𝑅 =( −1 +2𝜆,2𝜆,7 −𝜆). dist⁡(𝑃,𝑅)=|⃗𝑃𝑅|=√(−1+2𝜆)2+(2𝜆)2+(7−𝜆)2=√9𝜆2−18𝜆+50. Como queremos hallar los puntos de 𝑟 cuya distancia a 𝑃 sea de √50 𝑢, dist⁡(𝑃,𝑅)=√50⇔√9𝜆2−18𝜆+50=√50⇔9𝜆2−18𝜆+50=50⇔9𝜆(𝜆−2)=0⇔{𝜆=0,𝜆=2. Por tanto, los puntos son 𝑅1( −1,2,3) y 𝑅2(3,6,1).