Matemáticas de Selectividad

1. En primer lugar, hallamos las dos primeras derivadas de la función 𝑓. 𝑓′(𝑥)=𝑒𝑥+(𝑥−1)𝑒𝑥=𝑥𝑒𝑥,𝑓″(𝑥)=𝑒𝑥+𝑥𝑒𝑥=(𝑥+1)𝑒𝑥. Para hallar los candidatos a puntos de inflexión, igualamos la segunda derivada de 𝑓 a cero. 𝑓″(𝑥)=0⇔(𝑥+1)𝑒𝑥=0⇔𝑥+1=0⇔𝑥=−1. Estudiamos el signo de la segunda derivada para comprobar si se trata de un punto de inflexión.

   	( −∞, −1)	( −1, +∞)
   signo de 𝑓″	−	+
   curvatura de 𝑓	⌢	⌣

   Así que el punto de inflexión de la función tiene abscisa 𝑥 = −1.
   • La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 = −1 viene dada por: 𝑦−𝑓(−1)=𝑓′(−1)(𝑥+1)⇔𝑦+2𝑒=−1𝑒(𝑥+1)⇔𝑦=−𝑥𝑒−3𝑒.
   • La ecuación de la recta normal a la gráfica de 𝑓 en 𝑥 = −1 viene dada por: 𝑦−𝑓(−1)=−1𝑓′(−1)(𝑥+1)⇔𝑦+2𝑒=𝑒(𝑥+1)⇔𝑦=𝑒𝑥+𝑒−2𝑒.
2. • La función no presenta ningún problema de dominio, así que no tiene ninguna asíntota vertical.
   • Estudiamos si 𝑓 tiene alguna asíntota horizontal estudiando sus límites en el infinito. lím𝑥→−∞⁡𝑓(𝑥)=lím𝑥→−∞⁡(𝑥−1)𝑒𝑥=0,lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡(𝑥−1)𝑒𝑥=+∞. Por tanto, la recta 𝑦 =0 es una asíntota horizontal en −∞ y no tiene asíntota horizontal en +∞. Así que no puede tener una asíntota oblicua en −∞.
   • Estudiamos si 𝑓 tiene una asíntota oblicua en +∞. lím𝑥→+∞⁡𝑓(𝑥)𝑥=lím𝑥→+∞⁡(𝑥−1)𝑒𝑥𝑥=+∞. Por tanto, 𝑓 no tiene ninguna asíntota oblicua.

1. Calculamos en primer lugar la pendiente de la recta que pasa por los puntos 𝐴(1,0) y 𝐵(𝑒,1). 𝑚=1−0𝑒−1=1𝑒−1. Por otro lado, la pendiente de la recta tangente a la gráfica de 𝑓 viene dada por el valor de su derivada. Calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=1𝑥. Hallamos los puntos en los que las pendientes coinciden. 𝑓′(𝑥)=1𝑒−1⇔1𝑥=1𝑒−1⇔𝑥=𝑒−1. Por tanto, la recta tangente es paralela a la recta dada en el punto (𝑒 −1,ln⁡(𝑒 −1)).
2. La pendiente 𝑚𝑡 de la recta tangente a la gráfica de 𝑓 en 𝑥 =1 viene dada por 𝑚𝑡=𝑓′(1)=1. Como la recta normal es perpendicular a la recta tangente, su pendiente 𝑚𝑛 es 𝑚𝑛=−1𝑚𝑡=−1. Por tanto, la ecuación de la recta normal a la gráfica de 𝑓 en el punto 𝐴(1,0) es 𝑦−0=𝑚𝑛(𝑥−1)⇔𝑦=−𝑥+1.

La función 𝑔(𝑥) =cos⁡(𝑥)sen2⁡(𝑥) es continua. Por el teorema fundamental del cálculo, la función 𝑓(𝑥)=∫𝑥0𝑔(𝑡)𝑑𝑡=∫𝑥0cos⁡(𝑡)sen2⁡(𝑡)𝑑𝑡 es derivable, con 𝑓′(𝑥) =𝑔(𝑥).

Hallamos el valor de la función y la derivada en 𝜋4. 𝑓(𝜋4)=∫𝜋40𝑔(𝑡)𝑑𝑡=∫𝜋40cos⁡(𝑡)sen2⁡(𝑡)𝑑𝑡=[13sen3⁡(𝑡)]𝜋40=13⋅√24=√212,𝑓′(𝜋4)=𝑔(𝜋4)=cos⁡(𝜋4)sen2⁡(𝜋4)=√24.

• La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =𝜋4 viene dada por: 𝑦−𝑓(𝜋4)=𝑓′(𝜋4)(𝑥−𝜋4)⇔𝑦−√212=√24(𝑥−𝜋4)⇔𝑦=√24𝑥+√212−√2𝜋16.
• La ecuación de la recta normal a la gráfica de 𝑓 en 𝑥 =𝜋4 viene dada por: 𝑦−𝑓(𝜋4)=−1𝑓′(𝜋4)(𝑥−𝜋4)⇔𝑦−√212=−4√2(𝑥−𝜋4)⇔𝑦=−2√2𝑥+√212+𝜋√2.

1. En primer lugar, observamos que 𝑓 es continua y derivable en cada una de sus ramas para cualquier valor de 𝑎 y 𝑏, con 𝑓′(𝑥)=⎧{ { {⎨{ { {⎩−𝑎𝑒−𝑥−𝑏1−𝑥,si 𝑥<0,1+11+𝑥,si 𝑥≥0. Pasamos a estudiar su continuidad y derivabilidad en el punto de ruptura 𝑥 =0.
   • Estudiamos la continuidad. lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0−⁡(𝑎𝑒−𝑥+𝑏ln⁡(1−𝑥))=𝑎,lím𝑥→0+⁡𝑓(𝑥)=lím𝑥→0+⁡(𝑥+ln⁡(1+𝑥))=0,𝑓(0)=0. Como 𝑓 es continua en 𝑥 =0, lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0+⁡𝑓(𝑥)=𝑓(0)⇔𝑎=0.
   • Estudiamos la derivabilidad. 𝑓′−(0)=lím𝑥→0−⁡𝑓′(𝑥)=lím𝑥→0−−𝑏1−𝑥=−𝑏,𝑓′+(0)=lím𝑥→0+⁡𝑓′(𝑥)=lím𝑥→0+⁡1+11+𝑥=2. Como 𝑓 es derivable en 𝑥 =0, 𝑓′−(0)=𝑓′+(0)⇔−𝑏=2⇔𝑏=−2.
   Así que 𝑎 =0 y 𝑏 = −2.
2. • La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =0 es: 𝑦−𝑓(0)=𝑓′(0)(𝑥−0)⇔𝑦=2𝑥.
   • La recta normal a la gráfica de 𝑓 en 𝑥 =0 tiene como pendiente −1𝑓′(0). Por tanto, su ecuación es: 𝑦−𝑓(0)=−1𝑓′(0)(𝑥−0)⇔𝑦=−12𝑥.

1. Calculamos en primer lugar la pendiente de la recta que pasa por los puntos ( −2,𝑓( −2)) =( −2,1) y (2,𝑓(2)) =(2,9). 𝑚=9−12−(−2)=2. Por otro lado, la pendiente de la recta tangente a la gráfica de 𝑓 en un punto 𝑎 viene dada por el valor de 𝑓′(𝑎). La derivada de 𝑓 es 𝑓′(𝑥) =3𝑥2 −2. Hallemos los puntos en los que la pendiente de la recta tangente es 2. 𝑓′(𝑥)=2⇔3𝑥2−2=2⇔3𝑥2=4⇔𝑥=±√43=±2√3. Por tanto, las abscisas de los puntos en los que las pendientes coinciden son 𝑥1 = −2√3 y 𝑥2 =2√3.
2. Calculamos en primer lugar la segunda derivada de 𝑓. 𝑓″(𝑥)=6𝑥. Para hallar el punto de inflexión, igualamos la segunda derivada de 𝑓 a cero. 𝑓″(𝑥)=0⇔6𝑥=0⇔𝑥=0. Así que en 𝑥 =0 se encuentra el único punto de inflexión. La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =0 es 𝑦−𝑓(0)=𝑓′(0)(𝑥−0)⇔𝑦−5=−2𝑥⇔𝑦=−2𝑥+5. La recta normal a la gráfica de 𝑓 tiene como pendiente −1𝑓′(0). Por tanto, su ecuación es 𝑦−𝑓(0)=−1𝑓′(0)(𝑥−0)⇔𝑦−5=12𝑥⇔𝑦=12𝑥+5.

En primer lugar, expresamos la función 𝑓 como función a trozos. 𝑓(𝑥)=𝑥|𝑥−1|={−𝑥(𝑥−1)=−𝑥2+𝑥,si 𝑥<1,𝑥(𝑥−1)=𝑥2−𝑥,si 𝑥≥1.

La pendiente de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0 viene dada por el valor de 𝑓′(0). Si 𝑥 >1, la derivada de 𝑓 es 𝑓′(𝑥) =2𝑥 −1. Por tanto, la ecuación de la recta tangente es 𝑦−𝑓(0)=𝑓′(0)(𝑥−0)⇔𝑦=𝑥.

Calculamos los puntos de corte de la función con la recta. {𝑦=𝑥2−𝑥𝑦=𝑥⇒𝑥2−𝑥=𝑥⇔𝑥(𝑥−2)=0⇔{𝑥1=0,𝑥2=2.

Representamos la función 𝑓 y la recta 𝑦 =𝑥 para visualizar el área del recinto.

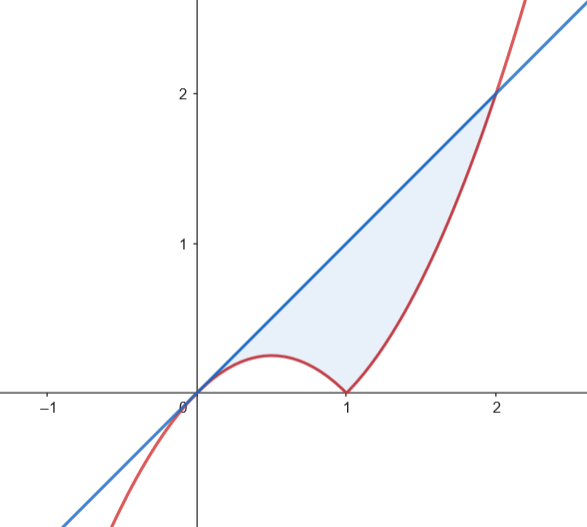
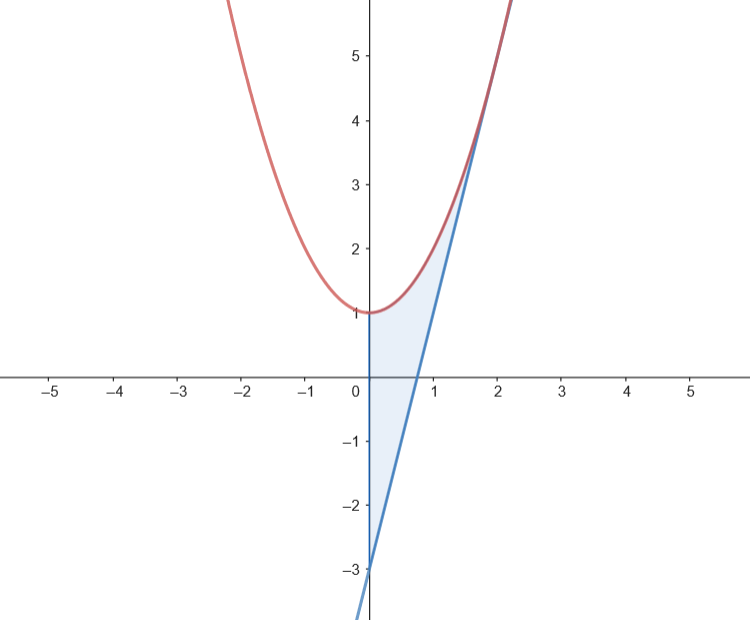Por último, calculamos el área del recinto. ∫20(𝑥−𝑓(𝑥))𝑑𝑥=∫10(𝑥−(−𝑥2+𝑥))𝑑𝑥+∫21(𝑥−(𝑥2−𝑥))𝑑𝑥=∫10𝑥2𝑑𝑥+∫21(−𝑥2+2𝑥)𝑑𝑥==[𝑥33]10+[−𝑥33+𝑥2]21=1𝑢2.

1. En primer lugar, calculamos la derivada de 𝑓. 𝑓′(𝑥)=2𝑥. La pendiente de la recta tangente viene dada por el valor de la derivada. Veamos en qué punto es igual a 4. 𝑓′(𝑥)=4⇔2𝑥=4⇔𝑥=2. Luego el único candidato es el punto (2,5). Podemos comprobar que, efectivamente, la ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =2 es 𝑦−𝑓(2)=𝑓′(2)(𝑥−2)→𝑦−5=4(𝑥−2)⇔𝑦=4𝑥−3.
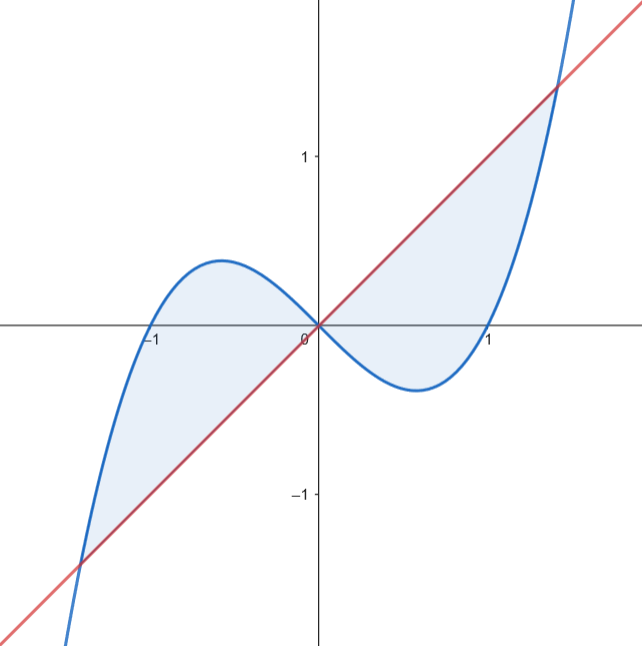
2. Sabemos por el apartado anterior que la función y la recta se cortan en 𝑥 =2. Representamos el recinto. 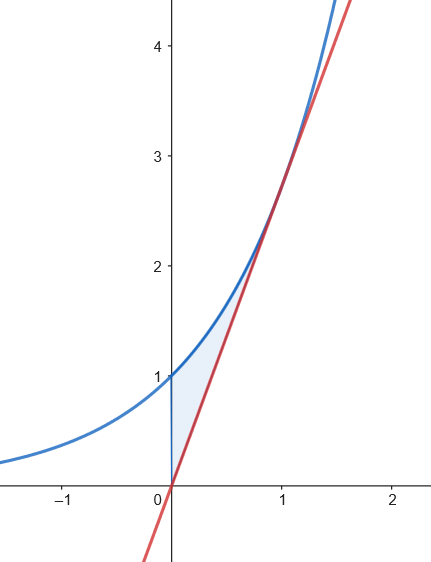Calculamos el área del recinto. ∫20((𝑥2+1)−(4𝑥−3))𝑑𝑥=∫20(𝑥2−4𝑥+4)𝑑𝑥=[𝑥33−2𝑥2+4𝑥]20=83𝑢2.

1. Por un lado, si la gráfica de 𝑓 pasa por el punto (1, −2), entonces 𝑓(1) = −2. Así que 𝑓(1)=−2⇔1+𝑎1−𝑏=−2⇔1+𝑎=2𝑏−2. Por otro lado, la gráfica de 𝑓 tiene una asíntota oblicua de pendiente 𝑚 =1 y ordenada en el origen 𝑛 =4. La pendiente viene dada por el límite lím𝑥→∞⁡𝑓(𝑥)𝑥=𝑥2+𝑎𝑥2−𝑏𝑥=1. Como 𝑚 =1, la ordenada en el origen se calcula como lím𝑥→∞⁡(𝑓(𝑥)−𝑥)=lím𝑥→∞⁡𝑥2+𝑎−𝑥2+𝑏𝑥𝑥−𝑏=lím𝑥→∞⁡𝑎+𝑏𝑥𝑥−𝑏=𝑏. Así que 𝑛=4⇔𝑏=4. Como 𝑏 =4, sustituyendo en la primera ecuación obtenemos que 1+𝑎=2𝑏−2⇔𝑎=2𝑏−3𝑏=4←←←←←←→𝑎=5.
2. Si 𝑎 =5 y 𝑏 =4, 𝑓(𝑥)=𝑥2+5𝑥−4. En primer lugar, calculamos su derivada. 𝑓′(𝑥)=2𝑥(𝑥−4)−𝑥2−5(𝑥−4)2=2𝑥2−8𝑥−𝑥2−5(𝑥−4)2=𝑥2−8𝑥−5(𝑥−4)2. La pendiente 𝑚𝑡 de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0 viene dada por 𝑚𝑡=𝑓′(0)=−516. Como la recta normal es perpendicular a la recta tangente, su pendiente 𝑚𝑛 ha de verificar 𝑚𝑡⋅𝑚𝑛=−1⇔𝑚𝑛=−1𝑚𝑡𝑚𝑡=−5/16←←←←←←←←←←←←←←→𝑚𝑛=165. Por tanto, la recta normal a la gráfica de 𝑓 en 𝑥 =0 se puede hallar usando la ecuación punto-pendiente como 𝑦−𝑓(0)=𝑚𝑛(𝑥−0)⇔𝑦+54=516𝑥⇔𝑦=516𝑥−54.

1. En primer lugar, calculamos la derivada de 𝑓. 𝑓′(𝑥)={5,si −2≤𝑥<0,𝑒𝑥(cos⁡(𝑥)−sen⁡(𝑥)),si 0<𝑥≤2𝜋. Para hallar los puntos críticos, igualamos las dos ramas de la derivada de 𝑓 a cero.
   • Si −2 ≤𝑥 <0, 𝑓′(𝑥) =5 ≠0.
   • Si 0 <𝑥 ≤2𝜋, 𝑓′(𝑥)=0⇔𝑒𝑥(cos⁡(𝑥)−sen⁡(𝑥))=0⇔cos⁡(𝑥)−sen⁡(𝑥)=0⇔cos⁡(𝑥)=sen⁡(𝑥)⇔{𝑥=𝜋4,𝑥=5𝜋4.
   Así que los puntos críticos son 𝑥 =𝜋4 y 𝑥 =5𝜋4. También consideraremos 𝑥 =0 por ser el punto de ruptura. Estudiamos el signo de la derivada para determinar si se tratan de extremos.

   	( −2,0)	(0,𝜋4)	(𝜋4,5𝜋4)	(5𝜋4,2𝜋)
   signo de 𝑓′	+	+	−	+
   monotonía de 𝑓	→	→	→	→

   Por tanto, considerando también los extremos del intervalo, 𝑓 tiene máximos relativos en 𝑥 =𝜋4 y 𝑥 =2𝜋 y tiene mínimos relativos en 𝑥 = −2 y 𝑥 =5𝜋4. Es decir, los puntos (𝜋4,𝑒𝜋4√22) y (2𝜋,𝑒2𝜋) son máximos relativos y los puntos ( −2, −9) y (5𝜋4,−𝑒5𝜋4√22) son mínimos relativos. Comparando, podemos concluir que el punto (2𝜋,𝑒2𝜋) es un máximo absoluto y el punto (5𝜋4,−𝑒5𝜋4√22) es un mínimo absoluto.
2. La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =𝜋2 es 𝑦−𝑓(𝜋2)=𝑓′(𝜋2)(𝑥−𝜋2)→𝑦=−𝑒𝜋2(𝑥−𝜋2)⇔𝑦=−𝑒𝜋2𝑥+𝑒𝜋2𝜋2.