Icono Matemáticas de Selectividad

Buscar GitHub

📋 Junio de 2021

Ejercicio 1

Se sabe que la gráfica de la función 𝑓 definida por 𝑓(𝑥)=𝑎𝑥2+𝑏𝑥+2𝑥−1 (para 𝑥 ≠1) tiene una asíntota oblicua que pasa por el punto (1,1) y tiene pendiente 2. Calcula 𝑎 y 𝑏.

Resolución

La asíntota oblicua tiene pendiente 𝑚 =2, así que su ecuación es de la forma 𝑦=2𝑥+𝑛. Como además pasa por el punto (1,1), entonces 1=2+𝑛⇔𝑛=−1. Así que su ecuación es 𝑦 =2𝑥 −1.

Hallamos de manera analítica la asíntota oblicua. La pendiente de la asíntota viene dada por el límite lím𝑥→∞⁡𝑓(𝑥)𝑥=𝑎𝑥2+𝑏𝑥+2𝑥2−𝑥=𝑎, así que 𝑎 =2.

Por otro lado, como 𝑚 =2, la ordenada en el origen de la asíntota se calcula como lím𝑥→∞⁡(𝑓(𝑥)−2𝑥)=lím𝑥→∞⁡2𝑥2+𝑏𝑥+2−2𝑥2−2𝑥𝑥−1=lím𝑥→∞⁡(𝑏+2)𝑥+2𝑥−1=𝑏+2. Por tanto, 𝑏+2=−1⇔𝑏=−3.

Ejercicio 2

Considera la función continua 𝑓 :ℝ →ℝ definida por 𝑓(𝑥)=⎧{ {⎨{ {⎩(3𝑥−6)𝑒𝑥,si 𝑥≤0,36(sen⁡(𝑥)−𝑎𝑥)𝑥3,si 𝑥>0.

  1. Calcula 𝑎.
  2. Halla la ecuación de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 = −1.

Resolución
  1. En primer lugar, observamos que 𝑓 es continua en cada una de sus ramas para cualquier valor de 𝑎. Pasamos a estudiar su continuidad en 𝑥 =0. lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0−⁡(3𝑥−6)𝑒𝑥=−6,lím𝑥→0+⁡𝑓(𝑥)=lím𝑥→0+⁡36(sen⁡(𝑥)−𝑎𝑥)𝑥3=00→lím𝑥→0+⁡36(sen⁡(𝑥)−𝑎𝑥)𝑥3L’H=lím𝑥→0+⁡36(cos⁡(𝑥)−𝑎)3𝑥2=36(1−𝑎)0,𝑓(0)=−6. Si 𝑎 ≠1 el segundo límite será infinito y la función no será continua en 𝑥 =0, así que necesariamente 𝑎 =1. Continuamos resolviendo el límite para 𝑎 =1. lím𝑥→0+⁡36(cos⁡(𝑥)−1)3𝑥2L’H=lím𝑥→0+⁡−36sen⁡(𝑥)6𝑥L’H=lím𝑥→0+⁡−36cos⁡(𝑥)6=−366=−6. Observamos que para este valor de 𝑎 se verifica que lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0+⁡𝑓(𝑥)=𝑓(0).
  2. La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 = −1 viene dada por 𝑦−𝑓(−1)=𝑓′(−1)(𝑥+1). Como para 𝑥 ≤0 la derivada de la función es 𝑓′(𝑥)=3𝑒𝑥+(3𝑥−6)𝑒𝑥=(3𝑥−3)𝑒𝑥, entonces 𝑓′( −1) = −6𝑒. Por tanto, la ecuación de la recta tangente en 𝑥 = −1 es 𝑦+9𝑒=−6𝑒(𝑥+1)⇔𝑦=−6𝑒𝑥−15𝑒.

Ejercicio 3

Considera la función 𝑓 :ℝ →ℝ definida por 𝑓(𝑥) =4𝑥3 −𝑥4.

  1. Determina los intervalos de crecimiento y decrecimiento de 𝑓.
  2. Esboza la gráfica de 𝑓 y calcula el área del recinto limitado por dicha gráfica y el eje de abscisas.

Resolución
  1. En primer lugar, calculamos la derivada de 𝑓. 𝑓′(𝑥)=12𝑥2−4𝑥3. Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔12𝑥2−4𝑥3=0⇔4𝑥2(3−𝑥)=0⇔{𝑥=0,3−𝑥=0⇔𝑥=3. Estudiamos el signo de 𝑓′.
    • Si 𝑥 <0, 𝑓′(𝑥) >0. Así que 𝑓 es creciente.
    • Si 0 <𝑥 <3, 𝑓′(𝑥) >0. Así que 𝑓 es creciente.
    • Si 𝑥 >3, 𝑓′(𝑥) <0. Así que 𝑓 es decreciente.
    Por tanto, 𝑓 es creciente en ( −∞,3) y es decreciente en (3, +∞).
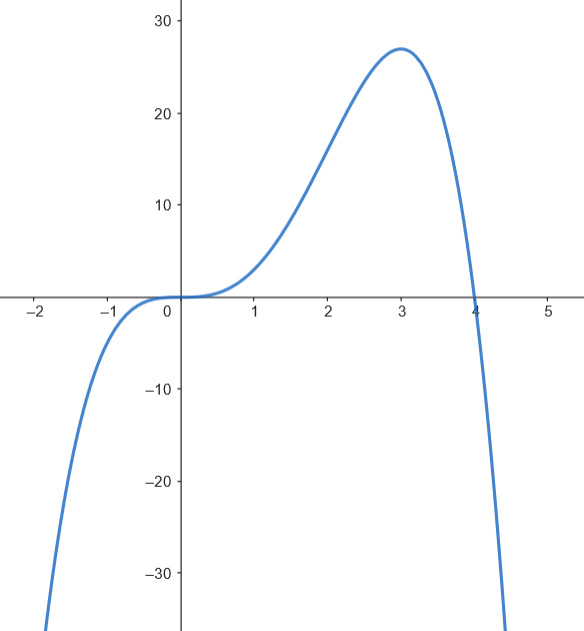  2. En primer lugar, hallamos los puntos de corte de la función 𝑓 con el eje 𝑋. 𝑓(𝑥)=0⇔4𝑥3−𝑥4=0⇔𝑥3(4−𝑥)=0⇔{𝑥=0,4−𝑥=0⇔𝑥=4. Así que los puntos de corte con (0,0) y (4,0). Representamos gráficamente la función. Figura Podemos representar gráficamente el recinto limitado por la gráfica de 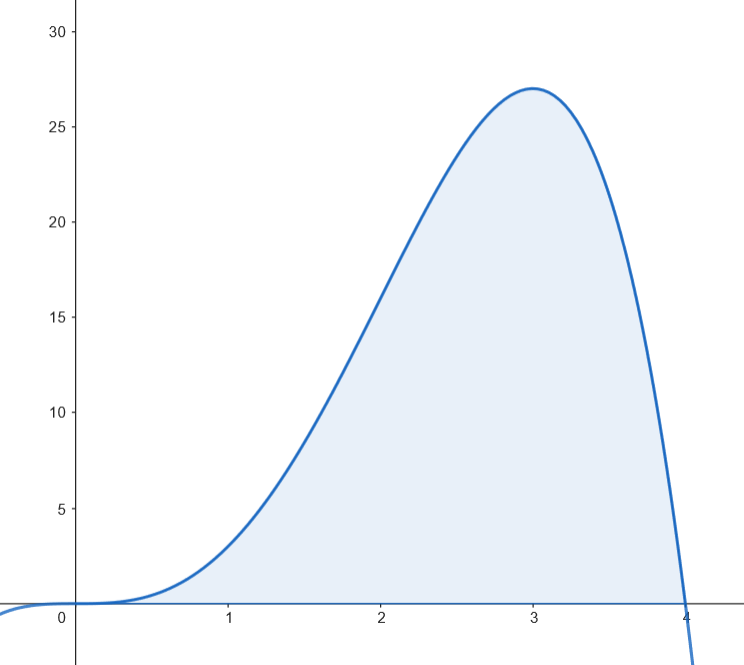𝑓 y el eje 𝑋. Figura Calculamos el área. ∫40𝑓(𝑥)𝑑𝑥=∫40(4𝑥3−𝑥4)𝑑𝑥=[𝑥4−15𝑥5]40=2565𝑢2.

Ejercicio 4

Considera la función 𝐹 :[0, +∞) →ℝ definida por 𝐹(𝑥)=∫𝑥0(2𝑡+√𝑡)𝑑𝑡. Halla la ecuación de la recta tangente a la gráfica de 𝐹 en el punto de abscisa 𝑥 =1.

Resolución

La función 𝑓(𝑥) =2𝑥 +√𝑥 es continua si 𝑥 ≥0. Por el teorema fundamental del cálculo, la función 𝐹(𝑥)=∫𝑥0𝑓(𝑡)𝑑𝑡=∫𝑥0(2𝑡+√𝑡)𝑑𝑡 es derivable, con 𝐹′(𝑥) =𝑓(𝑥).$

La ecuación de la recta tangente a la gráfica de 𝐹 en 𝑥 =1 viene dada por 𝑦−𝐹(1)=𝐹′(1)(𝑥−1). Por un lado, 𝐹′(1)=𝑓(1)=3. Por otro lado, 𝐹(1)=∫10𝑓(𝑡)𝑑𝑡=∫10(2𝑡+√𝑡)𝑑𝑡=[𝑡2+23𝑡32]10=1+23=53.

Por tanto, la ecuación de la recta tangente en 𝑥 =1 es 𝑦−53=3(𝑥−1)⇔𝑦=3𝑥−3+53⇔𝑦=3𝑥−43.

Ejercicio 5

Considera el siguiente sistema de ecuaciones lineales ⎧{ {⎨{ {⎩𝑚𝑥+2𝑦−𝑧=1,5𝑥−4𝑦+2𝑧=0,𝑥+3𝑚𝑦=𝑚+25.

  1. Discute el sistema según los valores de 𝑚.
  2. Resuelve el sistema para 𝑚 =0. ¿Hay alguna solución en la que 𝑥 =0? En caso afirmativo, calcúlala. En caso negativo, justifica la respuesta.

Resolución
  1. La matriz de coeficientes del sistema es 𝐴=⎛⎜ ⎜ ⎜⎝𝑚2−15−4213𝑚0⎞⎟ ⎟ ⎟⎠. Observamos que ∣5210∣=−2≠0⇒rang⁡(𝐴)≥2. Para determinar el rango de 𝐴 en función del valor de 𝑚, estudiamos su determinante. |𝐴|=∣𝑚2−15−4213𝑚0∣=4−15𝑚−4−6𝑚2=−6𝑚2−15𝑚. Podemos ver que |𝐴|=0⇔−6𝑚2−15𝑚=0⇔𝑚(6𝑚+15)=0⇔{𝑚=0,6𝑚+15=0⇔𝑚=−156=−52. Así que, si 𝑚 ≠ −52 y 𝑚 ≠0, entonces rang⁡(𝐴) =3. En caso contrario, rang⁡(𝐴) =2. Por tanto,
    • Si 𝑚 ≠ −52 y 𝑚 ≠0, el rango de la matriz de coeficientes es máximo. Por el teorema de Rouché-Frobenius, el sistema es compatible determinado.
    • Si 𝑚 = −52, la matriz de coeficientes ampliada es 𝐴∗=⎛⎜ ⎜ ⎜ ⎜ ⎜⎝−522−115−4201−1520−2110⎞⎟ ⎟ ⎟ ⎟ ⎟⎠. Observamos que ∣ ∣ ∣ ∣2−11−420−1520−2110∣ ∣ ∣ ∣=15≠0⇒rang⁡(𝐴∗)=3. Como los rangos no coinciden, el sistema es incompatible.
    • Si 𝑚 =0, la matriz de coeficientes ampliada es 𝐴∗=⎛⎜ ⎜ ⎜ ⎜⎝02−115−42010025⎞⎟ ⎟ ⎟ ⎟⎠. Observamos que ∣ ∣ ∣ ∣2−11−4200025∣ ∣ ∣ ∣=0⇒rang⁡(𝐴∗)=2. Como rang⁡(𝐴) =rang⁡(𝐴∗) <3, el sistema es compatible indeterminado.
  2. Si 𝑚 =0, el sistema es compatible indeterminado por el apartado anterior, así que tiene infinitas soluciones. Resolvemos el sistema mediante el método de Gauss. ⎛⎜ ⎜ ⎜ ⎜⎝02−115−42010025⎞⎟ ⎟ ⎟ ⎟⎠𝐹2−5𝐹3←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜⎝02−110−42−210025⎞⎟ ⎟ ⎟ ⎟⎠𝐹2+2𝐹1←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜⎝02−11000010025⎞⎟ ⎟ ⎟ ⎟⎠→(02−1110025). El sistema resultante es {2𝑦−𝑧=1,𝑥=25. Si tomamos 𝑦 =𝜆, entonces 2𝑦−𝑧=1⇔𝑧=2𝑦−1𝑦=𝜆←←←←←←→𝑧=2𝜆−1. Por tanto, las soluciones del sistema son de la forma ⎧{ {⎨{ {⎩𝑥=25,𝑦=𝜆,𝑧=2𝜆−1,𝜆∈ℝ. Observamos que no existe ninguna solución con 𝑥 =0.

Ejercicio 6

En una empresa se fabrican tres tipos de productos plásticos: botellas, garrafas y bidones. Se utiliza como materia prima 10 kg de polietileno cada hora. Se sabe que para fabricar cada botella se necesitan 50 gramos, para cada garrafa 100 gramos y 1 kg para cada bidón. El gerente también nos dice que se debe producir el doble de botellas que de garrafas. Por último, se sabe que por motivos de capacidad de trabajo, en las máquinas se producen en total 52 productos cada hora. ¿Cuántas botellas, garrafas y bidones se producen cada hora?

Resolución

Llamamos 𝑥 al número de botellas producidas por hora, 𝑦 al número de garrafas y 𝑧 al número de bidones.

En primer lugar, si se dispone de 10 kilos de polietileno y se necesitan 50 gramos, 100 gramos y 1 kilo para cada botella, garrafa y bidón, respectivamente, entonces 50𝑥+100𝑦+1000𝑧=10000. Además, si se produce el doble de botellas que de garrafas, 𝑥=2𝑦. Por último, si se producen un total de 52 productos por hora, 𝑥+𝑦+𝑧=52.

Por tanto, podemos plantear el sistema de ecuaciones lineales ⎧{ {⎨{ {⎩50𝑥+100𝑦+1000𝑧=10000,𝑥=2𝑦,𝑥+𝑦+𝑧=52⇒⎧{ {⎨{ {⎩𝑥+2𝑦+20𝑧=200,𝑥−2𝑦=0,𝑥+𝑦+𝑧=52.

Resolvemos el sistema mediante el método de Gauss. ⎛⎜ ⎜ ⎜ ⎜⎝12202001−20011152⎞⎟ ⎟ ⎟ ⎟⎠𝐹1−20𝐹2←←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜⎝−19−180−8401−20011152⎞⎟ ⎟ ⎟ ⎟⎠𝐹1−9𝐹2←←←←←←←←←→⎛⎜ ⎜ ⎜ ⎜⎝−2800−8401−20011152⎞⎟ ⎟ ⎟ ⎟⎠. El sistema resultante es ⎧{ {⎨{ {⎩−28𝑥=−840,𝑥−2𝑦=0,𝑥+𝑦+𝑧=52.

Por tanto, −28𝑥=−840⇔𝑥=30,𝑥−2𝑦=0𝑥=30←←←←←←←→30−2𝑦=0⇔𝑦=15,𝑥+𝑦+𝑧=52𝑥=30←←←←←←←→𝑦=1530+15+𝑧=52⇔𝑧=7. Así que se producen 30 botellas, 15 garrafas y 7 bidones por hora.

Ejercicio 7

Considera las rectas 𝑟≡{2𝑥−3𝑦+𝑧−2=0,−3𝑥+2𝑦+2𝑧+1=0y𝑠≡⎧{ {⎨{ {⎩𝑥=3−2𝜆,𝑦=−1+𝜆,𝑧=−2+2𝜆.

  1. Calcula el plano perpendicular a la recta 𝑠 que pasa por el punto 𝑃(1,0, −5).
  2. Calcula el seno del ángulo que forma la recta 𝑟 con el plano 𝜋 ≡ −2𝑥 +𝑦 +2𝑧 =0.

Resolución
  1. El plano 𝜏 perpendicular a la recta 𝑠 tiene como vector normal ⃗𝑛𝜏 =⃗𝑑𝑠 =( −2,1,2). Si además pasa por el punto 𝑃(1,0, −5), entonces 𝜏≡−2(𝑥−1)+𝑦+2(𝑧+5)=0⇔−2𝑥+𝑦+2𝑧+12=0.
  2. En primer lugar, hallamos el vector director de la recta 𝑟. ⃗𝑑𝑟=(2,−3,1)×(−3,2,2)=∣ ∣ ∣ ∣⃗𝑖⃗𝑗⃗𝑘2−31−322∣ ∣ ∣ ∣=(−8,−7,−5). Además, el vector normal del plano 𝜋 es ⃗𝑛𝜋 =( −2,1,2). Por tanto, el seno del ángulo 𝛼 que forman el plano 𝜋 y la recta 𝑟 viene dado por sen⁡(𝛼)=|⃗𝑑𝑟⋅⃗𝑛𝜋||⃗𝑑𝑟||⃗𝑛𝜋|=1√138√9=13√138.

Ejercicio 8

La recta 𝑟≡𝑥+32=𝑦+42=𝑧−33 y la recta 𝑠, que pasa por los puntos 𝑃(1,0,2) y 𝑄(𝑎,1,0), se cortan en un punto. Calcula el valor de 𝑎 y el punto de corte.

Resolución

El vector director de la recta 𝑟 es ⃗𝑑𝑟 =(2,2,3). La recta 𝑠 pasa por 𝑃(1,0,2) y 𝑄(𝑎,1,0), así que su vector director es ⃗𝑑𝑠 =⃗𝑃𝑄 =(𝑎 −1,1, −2). Observamos que los vectores directores no pueden ser proporcionales, así que las dos rectas no son paralelas ni coincidentes. Tomamos un punto 𝑅( −3, −4,3) de 𝑟. Las dos rectas se cortan si están contenidas en un mismo plano, es decir, si ⃗𝑑𝑟, ⃗𝑑𝑠 y ⃗𝑅𝑃 =(4,4, −1) son linealmente dependientes. ∣223𝑎−11−244−1∣=−2+12(𝑎−1)−16−12+16+2(𝑎−1)=14𝑎−28. Los tres vectores son linealmente dependientes si y solo si 14𝑎−28=0⇔𝑎=2. Por tanto, 𝑟 y 𝑠 se cortan si y solo si 𝑎 =2.

Para hallar su punto de corte, primero escribimos las ecuaciones paramétricas de 𝑟 y 𝑠 para 𝑎 =2. 𝑟≡⎧{ {⎨{ {⎩𝑥=−3+2𝜆,𝑦=−4+2𝜆,𝑧=3+3𝜆y𝑠≡⎧{ {⎨{ {⎩𝑥=1+𝜇,𝑦=𝜇,𝑧=2−2𝜇. Calculamos el punto de corte igualando las ecuaciones entre sí. ⎧{ {⎨{ {⎩−3+2𝜆=1+𝜇,−4+2𝜆=𝜇,3+3𝜆=2−2𝜇. Resolvemos este sistema por sustitución. 3+3𝜆=2−2𝜇𝜇=−4+2𝜆←←←←←←←←←←←→3+3𝜆=2−2(−4+2𝜆)⇔3+3𝜆=10−4𝜆⇔7𝜆=7⇔𝜆=1. Por tanto, el punto de corte es 𝐶( −1, −2,6).