Matemáticas de Selectividad

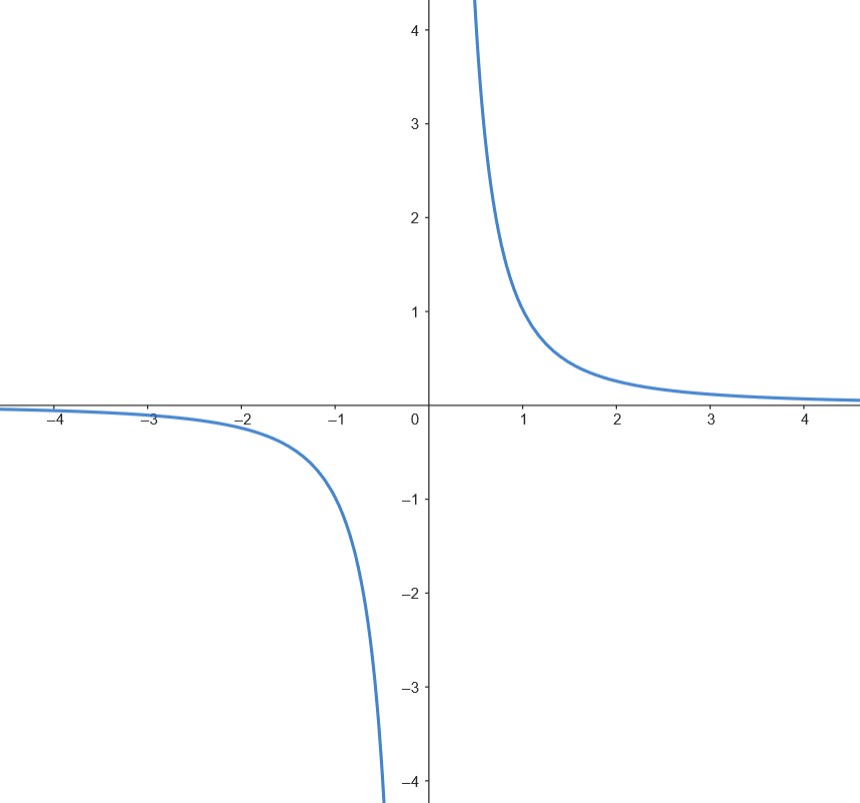
1. La ordenada de la asíntota horizontal viene dada por: lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡(𝑎+ln⁡(𝑥)𝑥2)=𝑎. Para que 𝑦 =1 sea la asíntota horizontal, ha de verificarse que 𝑎 =1.
2. En primer lugar, hallamos la derivada de la función 𝑓. 𝑓′(𝑥)=1𝑥⋅𝑥2−ln⁡(𝑥)⋅2𝑥𝑥4=𝑥−2𝑥ln⁡(𝑥)𝑥4=1−2ln⁡(𝑥)𝑥3. Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔1−2ln⁡(𝑥)𝑥3=0⇔1−2ln⁡(𝑥)=0⇔ln⁡(𝑥)=12⇔𝑥=√𝑒. Estudiamos el signo de la derivada.

   	(0,√𝑒)	(√𝑒, +∞)
   signo de 𝑓′	+	−
   monotonía de 𝑓	→	→

   Por tanto, 𝑓 es creciente en (0,√𝑒) y decreciente en (√𝑒, +∞). Además, el punto (√𝑒,12𝑒) es un máximo relativo.

1. En primer lugar, hallamos las dos primeras derivadas de la función 𝑓. 𝑓′(𝑥)=𝑒𝑥+(𝑥−1)𝑒𝑥=𝑥𝑒𝑥,𝑓″(𝑥)=𝑒𝑥+𝑥𝑒𝑥=(𝑥+1)𝑒𝑥. Para hallar los candidatos a puntos de inflexión, igualamos la segunda derivada de 𝑓 a cero. 𝑓″(𝑥)=0⇔(𝑥+1)𝑒𝑥=0⇔𝑥+1=0⇔𝑥=−1. Estudiamos el signo de la segunda derivada para comprobar si se trata de un punto de inflexión.

   	( −∞, −1)	( −1, +∞)
   signo de 𝑓″	−	+
   curvatura de 𝑓	⌢	⌣

   Así que el punto de inflexión de la función tiene abscisa 𝑥 = −1.
   • La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 = −1 viene dada por: 𝑦−𝑓(−1)=𝑓′(−1)(𝑥+1)⇔𝑦+2𝑒=−1𝑒(𝑥+1)⇔𝑦=−𝑥𝑒−3𝑒.
   • La ecuación de la recta normal a la gráfica de 𝑓 en 𝑥 = −1 viene dada por: 𝑦−𝑓(−1)=−1𝑓′(−1)(𝑥+1)⇔𝑦+2𝑒=𝑒(𝑥+1)⇔𝑦=𝑒𝑥+𝑒−2𝑒.
2. • La función no presenta ningún problema de dominio, así que no tiene ninguna asíntota vertical.
   • Estudiamos si 𝑓 tiene alguna asíntota horizontal estudiando sus límites en el infinito. lím𝑥→−∞⁡𝑓(𝑥)=lím𝑥→−∞⁡(𝑥−1)𝑒𝑥=0,lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡(𝑥−1)𝑒𝑥=+∞. Por tanto, la recta 𝑦 =0 es una asíntota horizontal en −∞ y no tiene asíntota horizontal en +∞. Así que no puede tener una asíntota oblicua en −∞.
   • Estudiamos si 𝑓 tiene una asíntota oblicua en +∞. lím𝑥→+∞⁡𝑓(𝑥)𝑥=lím𝑥→+∞⁡(𝑥−1)𝑒𝑥𝑥=+∞. Por tanto, 𝑓 no tiene ninguna asíntota oblicua.

1. La recta 𝑦 =𝑥 −2 tiene pendiente 𝑚 =1 y ordenada en el origen 𝑛 = −2. La pendiente de la asíntota oblicua de la gráfica de 𝑓 viene dada por: lím𝑥→+∞⁡𝑓(𝑥)𝑥=lím𝑥→+∞⁡𝑎𝑥3+𝑥−1𝑥3+𝑏𝑥2−3𝑥=𝑎. Para que tenga pendiente 1, tiene que ocurrir que 𝑎 =1. Por otro lado, la ordenada en el origen de la asíntota oblicua viene dada por: lím𝑥→+∞⁡(𝑓(𝑥)−𝑥)=lím𝑥→+∞⁡(𝑥3+𝑥−1𝑥2+𝑏𝑥−3−𝑥)=lím𝑥→+∞⁡−𝑏𝑥2+4𝑥−1𝑥2+𝑏𝑥−3=−𝑏. Para que su ordenada en el origen sea -2, tiene que verificarse que −𝑏 = −2 ⇔𝑏 =2. Por tanto, 𝑎 =1 y 𝑏 =2.
2. Si 𝑎 =0 y 𝑏 =2, 𝑓(𝑥)=𝑥−1𝑥2+2𝑥−3. Estudiamos en qué puntos se anula el denominador. 𝑥2+2𝑥−3=0⇔{𝑥=−3,𝑥=1. Así que podemos escribir la función 𝑓 como: 𝑓(𝑥)=𝑥−1(𝑥−1)(𝑥+3)=1𝑥+3. De esta forma, Dom⁡(𝑓) =ℝ ∖{ −3}. Observamos que: lím𝑥→−3−⁡𝑓(𝑥)=lím𝑥→−3−⁡1𝑥+3=10−=−∞,lím𝑥→−3+⁡𝑓(𝑥)=lím𝑥→−3+⁡1𝑥+3=10+=+∞. Por tanto, la recta 𝑥 = −3 es la única asíntota vertical de 𝑓.

La asíntota oblicua tiene pendiente 𝑚 =2 y pasa por el punto (0,1), así que su ecuación es 𝑦−1=2𝑥⇔𝑦=2𝑥+1.

Hallamos la asíntota oblicua analíticamente. La pendiente de la asíntota viene dada por el límite lím𝑥→+∞⁡𝑓(𝑥)𝑥=lím𝑥→+∞⁡𝑎𝑥3+𝑏𝑥2+𝑥−1𝑥3−𝑥=𝑎⇒𝑎=2. Por otro lado, la ordenada en el origen de la asíntota se calcula como lím𝑥→+∞⁡(𝑓(𝑥)−2𝑥)=lím𝑥→+∞⁡(2𝑥3+𝑏𝑥2+𝑥−1𝑥2−1−2𝑥)=lím𝑥→+∞⁡2𝑥3+𝑏𝑥2+𝑥−1−2𝑥3+2𝑥𝑥2−1==lím𝑥→+∞⁡𝑏𝑥2+3𝑥−1𝑥2−1=𝑏⇒𝑏=1. Por tanto, 𝑎 =2 y 𝑏 =1.

1. Por un lado, si la gráfica de 𝑓 pasa por el punto (1, −2), entonces 𝑓(1) = −2. Así que 𝑓(1)=−2⇔1+𝑎1−𝑏=−2⇔1+𝑎=2𝑏−2. Por otro lado, la gráfica de 𝑓 tiene una asíntota oblicua de pendiente 𝑚 =1 y ordenada en el origen 𝑛 =4. La pendiente viene dada por el límite lím𝑥→∞⁡𝑓(𝑥)𝑥=𝑥2+𝑎𝑥2−𝑏𝑥=1. Como 𝑚 =1, la ordenada en el origen se calcula como lím𝑥→∞⁡(𝑓(𝑥)−𝑥)=lím𝑥→∞⁡𝑥2+𝑎−𝑥2+𝑏𝑥𝑥−𝑏=lím𝑥→∞⁡𝑎+𝑏𝑥𝑥−𝑏=𝑏. Así que 𝑛=4⇔𝑏=4. Como 𝑏 =4, sustituyendo en la primera ecuación obtenemos que 1+𝑎=2𝑏−2⇔𝑎=2𝑏−3𝑏=4←←←←←→𝑎=5.
2. Si 𝑎 =5 y 𝑏 =4, 𝑓(𝑥)=𝑥2+5𝑥−4. En primer lugar, calculamos su derivada. 𝑓′(𝑥)=2𝑥(𝑥−4)−𝑥2−5(𝑥−4)2=2𝑥2−8𝑥−𝑥2−5(𝑥−4)2=𝑥2−8𝑥−5(𝑥−4)2. La pendiente 𝑚𝑡 de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0 viene dada por 𝑚𝑡=𝑓′(0)=−516. Como la recta normal es perpendicular a la recta tangente, su pendiente 𝑚𝑛 ha de verificar 𝑚𝑡⋅𝑚𝑛=−1⇔𝑚𝑛=−1𝑚𝑡𝑚𝑡=−5/16←←←←←←←←←←←←→𝑚𝑛=165. Por tanto, la recta normal a la gráfica de 𝑓 en 𝑥 =0 se puede hallar usando la ecuación punto-pendiente como 𝑦−𝑓(0)=𝑚𝑛(𝑥−0)⇔𝑦+54=516𝑥⇔𝑦=516𝑥−54.

1. En primer lugar, expresamos la función 𝑓 como función a trozos. 𝑓(𝑥)=⎧{ {⎨{ {⎩−1𝑥2,si 𝑥<0,1𝑥2,si 𝑥>0. Si 𝑥 ≠0, 𝑓 es derivable con 𝑓′(𝑥)=⎧{ {⎨{ {⎩2𝑥3,si 𝑥<0,−2𝑥3,si 𝑥>0y𝑓″(𝑥)=⎧{ {⎨{ {⎩−6𝑥4,si 𝑥<0,6𝑥4,si 𝑥>0. Observamos que 𝑓 no tiene puntos de inflexión, porque 𝑓″(𝑥) ≠0 para 𝑥 ≠0. Estudiamos el signo de la segunda derivada, considerando 𝑥 =0 por ser el punto de ruptura.

   	( −∞,0)	(0, +∞)
   signo de 𝑓″	−	+
   curvatura de 𝑓	⌢	⌣

   Por tanto, 𝑓 es convexa en (0, +∞) y es cóncava en ( −∞,0).
2. Estudiamos las asíntotas.
   • El denominador se anula en 𝑥 =0. Observamos que lím𝑥→0−⁡𝑓(𝑥)=lím𝑥→0−−1𝑥2=−∞,lím𝑥→0+⁡𝑓(𝑥)=lím𝑥→0+⁡1𝑥2=+∞. Por tanto, la recta 𝑥 =0 es una asíntota vertical.
   • Veamos si tiene alguna asíntota horizontal. lím𝑥→−∞⁡𝑓(𝑥)=lím𝑥→−∞−1𝑥2=0,lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡1𝑥2=0. Por tanto, la recta 𝑦 =0 es una asíntota horizontal y 𝑓 no tiene ninguna asíntota oblicua.
   Representamos gráficamente la función usando la información obtenida.

1. Calculamos en primer lugar la derivada de la función 𝑓. 𝑓′(𝑥)=3𝑥+4𝑥+1−3(ln⁡(𝑥+1)+𝑎)(3𝑥+4)2. Como la pendiente de la recta tangente a la gráfica de 𝑓 en 𝑥 =0 es 1, entonces 𝑓′(0) =1. 𝑓′(0)=1⇔4−3𝑎16=1⇔4−3𝑎=16⇔𝑎=−4.
2. Si 𝑎 =0, 𝑓(𝑥)=ln⁡(𝑥+1)3𝑥+4. Para determinar si la gráfica de 𝑓 tiene asíntotas verticales, analizamos los puntos que anulan el logaritmo o el denominador.
   • El denominador se anula si 𝑥 = −43. Sin embargo, la función no está definida en un entorno cercano.
   • El logaritmo se anula si 𝑥 = −1. Además, lím𝑥→−1+⁡ln⁡(𝑥+1)3𝑥+4=−∞. Por tanto, la recta 𝑥 = −1 es una asíntota vertical.
   Veamos si 𝑓 tiene alguna asíntota horizontal. Como Dom⁡(𝑓) =( −1, +∞), solo podría tener una asíntota horizontal por la derecha. lím𝑥→+∞⁡ln⁡(𝑥+1)3𝑥+4=0. Por tanto, la recta 𝑦 =0 es una asíntota horizontal y 𝑓 no tiene asíntotas oblicuas.

1. En primer lugar, observamos que 𝑓 es continua en cada una de sus ramas para cualquier valor de 𝑎 y 𝑏. Pasamos a estudiar su continuidad en 𝑥 = −1 y 𝑥 =1.
   • Si 𝑥 = −1, lím𝑥→−1−⁡𝑓(𝑥)=lím𝑥→−1−⁡1𝑥=−1,lím𝑥→−1+⁡𝑓(𝑥)=lím𝑥→−1+⁡(𝑎𝑥+𝑏)=−𝑎+𝑏,𝑓(−1)=−𝑎+𝑏. Como 𝑓 es continua en 𝑥 = −1, lím𝑥→−1−⁡𝑓(𝑥)=lím𝑥→−1+⁡𝑓(𝑥)=𝑓(−1)⇔−𝑎+𝑏=−1.
   • Si 𝑥 =1, lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1−⁡(𝑎𝑥+𝑏)=𝑎+𝑏,lím𝑥→1+⁡𝑓(𝑥)=lím𝑥→1+⁡𝑥2𝑥+1=12,𝑓(1)=12. Como 𝑓 es continua en 𝑥 =1, lím𝑥→1−⁡𝑓(𝑥)=lím𝑥→1+⁡𝑓(𝑥)=𝑓(1)⇔𝑎+𝑏=12.
   Por tanto, {−𝑎+𝑏=−1,𝑎+𝑏=12. Si sumamos las dos ecuaciones, obtenemos que 2𝑏=−12⇔𝑏=−14. Luego −𝑎+𝑏=−1𝑏=−1/4←←←←←←←←←→−𝑎−14=−1⇔𝑎=34. Así que 𝑎 =34 y 𝑏 = −14.
2. La función 𝑓 es continua en ℝ, así que su gráfica no tiene ninguna asíntota vertical. Falta estudiar la existencia de asíntotas horizontales y oblicuas.
   • Estudiamos las asíntotas por la izquierda. lím𝑥→−∞⁡𝑓(𝑥)=lím𝑥→−∞⁡1𝑥=0. Por tanto, 𝑦 =0 es una asíntota horizontal de la gráfica de 𝑓 por la izquierda.
   • Estudiamos las asíntotas por la derecha. lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡𝑥2𝑥+1=+∞. Así que no tiene una asíntota horizontal. Veamos si en su lugar tiene una asíntota oblicua. lím𝑥→+∞⁡𝑓(𝑥)𝑥=lím𝑥→+∞⁡𝑥𝑥+1=1. Así que 𝑓 tiene una asíntota oblicua con pendiente 𝑚 =1. Calculamos su ordenada en el origen. lím𝑥→+∞⁡(𝑓(𝑥)−𝑥)=lím𝑥→+∞⁡(𝑥2𝑥+1−𝑥)=lím𝑥→+∞⁡−𝑥𝑥+1=−1. Por tanto, 𝑦 =𝑥 −1 es una asíntota oblicua de la gráfica de 𝑓 por la derecha.