Icono Matemáticas de Selectividad

Buscar GitHub

📋 Reserva 2 de 2023

Ejercicio 1

Halla dos números mayores o iguales que 0, cuya suma sea 1, y el producto de uno de ellos por la raíz cuadrada del otro sea máximo.

Resolución

Llamamos 𝑥 e 𝑦 a los dos números, con 𝑥,𝑦 ≥0. Como 𝑥 +𝑦 =1, entonces 𝑦 =1 −𝑥. Así que la función a maximizar es 𝑓(𝑥)=𝑥⋅√𝑦=𝑥√1−𝑥.

En primer lugar, calculamos la derivada de la función 𝑓. 𝑓′(𝑥)=√1−𝑥−𝑥2√1−𝑥. Hallamos los puntos críticos de 𝑓 igualando la derivada a cero. 𝑓′(𝑥)=0⇔√1−𝑥−𝑥2√1−𝑥=0⇔1−𝑥=𝑥2⇔𝑥=23.

Comprobamos que en el punto de abscisa 𝑥 =23 se alcanza el máximo de la función.

(0,23) (23,1)
signo de 𝑓′ + −
monotonía de 𝑓 → →

Luego 𝑓 tiene un máximo en 𝑥 =23.

Por tanto, los números son 𝑥 =23 e 𝑦 =1 −𝑥 =13.

Ejercicio 2

Considera la función 𝑓(𝑥)=𝑥2+𝑎𝑥−𝑏, para 𝑥 ≠𝑏.

  1. Calcula 𝑎 y 𝑏 para que la gráfica de 𝑓 pase por el punto (1, −2) y tenga a la recta 𝑦 =𝑥 +4 como asíntota oblicua.
  2. En el caso 𝑎 =5 y 𝑏 =4, calcula la ecuación de la recta normal a la gráfica de 𝑓 que pasa por el punto de abscisa 𝑥 =0.

Resolución
  1. Por un lado, si la gráfica de 𝑓 pasa por el punto (1, −2), entonces 𝑓(1) = −2. Así que 𝑓(1)=−2⇔1+𝑎1−𝑏=−2⇔1+𝑎=2𝑏−2. Por otro lado, la gráfica de 𝑓 tiene una asíntota oblicua de pendiente 𝑚 =1 y ordenada en el origen 𝑛 =4. La pendiente viene dada por el límite lím𝑥→∞⁡𝑓(𝑥)𝑥=𝑥2+𝑎𝑥2−𝑏𝑥=1. Como 𝑚 =1, la ordenada en el origen se calcula como lím𝑥→∞⁡(𝑓(𝑥)−𝑥)=lím𝑥→∞⁡𝑥2+𝑎−𝑥2+𝑏𝑥𝑥−𝑏=lím𝑥→∞⁡𝑎+𝑏𝑥𝑥−𝑏=𝑏. Así que 𝑛=4⇔𝑏=4. Como 𝑏 =4, sustituyendo en la primera ecuación obtenemos que 1+𝑎=2𝑏−2⇔𝑎=2𝑏−3𝑏=4←←←←←→𝑎=5.
  2. Si 𝑎 =5 y 𝑏 =4, 𝑓(𝑥)=𝑥2+5𝑥−4. En primer lugar, calculamos su derivada. 𝑓′(𝑥)=2𝑥(𝑥−4)−𝑥2−5(𝑥−4)2=2𝑥2−8𝑥−𝑥2−5(𝑥−4)2=𝑥2−8𝑥−5(𝑥−4)2. La pendiente 𝑚𝑡 de la recta tangente a la gráfica de 𝑓 en el punto de abscisa 𝑥 =0 viene dada por 𝑚𝑡=𝑓′(0)=−516. Como la recta normal es perpendicular a la recta tangente, su pendiente 𝑚𝑛 ha de verificar 𝑚𝑡⋅𝑚𝑛=−1⇔𝑚𝑛=−1𝑚𝑡𝑚𝑡=−5/16←←←←←←←←←←←←→𝑚𝑛=165. Por tanto, la recta normal a la gráfica de 𝑓 en 𝑥 =0 se puede hallar usando la ecuación punto-pendiente como 𝑦−𝑓(0)=𝑚𝑛(𝑥−0)⇔𝑦+54=516𝑥⇔𝑦=516𝑥−54.

Ejercicio 3

Sabiendo que 𝐹 :ℝ →ℝ definida por 𝐹(𝑥) =𝑒𝑥2 es una primitiva de 𝑓.

  1. Comprueba que 𝑓 es creciente.
  2. Calcula el área del recinto limitado por la gráfica de la función 𝑓, el eje de abscisas y la recta 𝑥 =1.

Resolución
  1. Como 𝐹 es una primitiva de 𝑓, entonces 𝑓(𝑥)=𝐹′(𝑥)=2𝑥𝑒𝑥2. Calculamos en primer lugar la derivada de la función 𝑓. 𝑓′(𝑥)=2𝑒𝑥2+2𝑥⋅2𝑥𝑒𝑥2=2𝑒𝑥2(2𝑥2+1). Observamos que la derivada no se anula en ningún punto, así la función no tiene ningún punto crítico. Como 𝑓′(𝑥) >0 para todo 𝑥, 𝑓 es creciente en ℝ.
  2. Calculamos los puntos de corte de la función con el eje 𝑋. 𝑓(𝑥)=0⇔2𝑥𝑒𝑥2=0⇔𝑥=0. Podemos representar el recinto limitado por la gráfica de 𝑓, el eje 𝑋 y la recta 𝑥 =1. Figura Calculamos el área del recinto. ∫10𝑓(𝑥)𝑑𝑥=[𝐹(𝑥)]10=[𝑒𝑥2]10=𝑒−1𝑢2.

Ejercicio 4

Considera la función 𝑓 :[0, +∞) →ℝ definida por 𝑓(𝑥) =cos⁡(√𝑥). Calcula, si es posible, una primitiva de 𝑓 cuya gráfica pase por el punto (0,5). Sugerencia: haz el cambio 𝑡 =√𝑥.

Resolución

En primer lugar, hallamos todas las primitivas de la función 𝑓 usando el cambio de variable: 𝑡=√𝑥⇒𝑡2=𝑥,2𝑡𝑑𝑡=𝑑𝑥. De esta forma, 𝐹(𝑥)=∫cos⁡(√𝑥)𝑑𝑥=2∫𝑡cos⁡(𝑡)𝑑𝑡. Resolvemos la integral por partes. 𝑢=𝑡⇒𝑢′=1,𝑣′=cos⁡(𝑡)⇒𝑣=sen⁡(𝑡). Entonces: 𝐹(𝑥)=2∫𝑡cos⁡(𝑡)𝑑𝑡=2𝑡sen⁡(𝑡)−2∫sen⁡(𝑡)𝑑𝑡=2𝑡sen⁡(𝑡)+2cos⁡(𝑡)+𝐶=2√𝑥sen⁡(√𝑥)+2cos⁡(√𝑥)+𝐶.

La primitiva que pasa por el punto (0,5) ha de verificar: 𝐹(0)=5⇔2+𝐶=5⇔𝐶=3. Por tanto, la primitiva es: 𝐹(𝑥)=2𝑡sen⁡(√𝑥)+2cos⁡(√𝑥)+3.

Ejercicio 5

Considera la matriz 𝐴=⎛⎜ ⎜ ⎜⎝0𝑎−𝑏00𝑏000⎞⎟ ⎟ ⎟⎠.

  1. Calcula 𝐴10.
  2. Calcula, si es posible, la matriz inversa de 𝐼 +𝐴 +𝐴2, donde 𝐼 denota la matriz identidad de orden 3.

Resolución
  1. Calculamos las primeras potencias de 𝐴. 𝐴2=⎛⎜ ⎜ ⎜⎝00𝑎𝑏000000⎞⎟ ⎟ ⎟⎠y𝐴3=⎛⎜ ⎜ ⎜⎝000000000⎞⎟ ⎟ ⎟⎠. Como 𝐴3 es una matriz nula, entonces el resto de potencias serán también matrices nulas. Por tanto, 𝐴10=⎛⎜ ⎜ ⎜⎝000000000⎞⎟ ⎟ ⎟⎠.
  2. En primer lugar, hallamos la matriz. 𝐼+𝐴+𝐴2=⎛⎜ ⎜ ⎜⎝100010001⎞⎟ ⎟ ⎟⎠+⎛⎜ ⎜ ⎜⎝0𝑎−𝑏00𝑏000⎞⎟ ⎟ ⎟⎠+⎛⎜ ⎜ ⎜⎝00𝑎𝑏000000⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝1𝑎𝑎𝑏−𝑏01𝑏001⎞⎟ ⎟ ⎟⎠. Como det(𝐼 +𝐴 +𝐴2) =1 ≠0, la matriz es invertible. Para hallar su inversa, calculamos primero su matriz adjunta. Adj⁡(𝐼+𝐴+𝐴2)=⎛⎜ ⎜ ⎜⎝100−𝑎10𝑏−𝑏1⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular su inversa como (𝐼+𝐴+𝐴2)−1=1|𝐼+𝐴+𝐴2|Adj⁡(𝐼+𝐴+𝐴2)𝑡=⎛⎜ ⎜ ⎜⎝1−𝑎𝑏01−𝑏001⎞⎟ ⎟ ⎟⎠.

Ejercicio 6

Dadas las matrices 𝐴=⎛⎜ ⎜ ⎜⎝110101011⎞⎟ ⎟ ⎟⎠y𝐵=⎛⎜ ⎜ ⎜⎝001010100⎞⎟ ⎟ ⎟⎠, se define la matriz 𝑀 =𝐴 +(𝜆 −1)𝐵.

  1. Halla los valores de 𝜆 para los que la matriz 𝑀 tiene rango menor que 3.
  2. Para 𝜆 = −1, resuelve el sistema lineal homogéneo cuya matriz de coeficientes es 𝑀.

Resolución
  1. En primer lugar, calculamos 𝑀. 𝑀=⎛⎜ ⎜ ⎜⎝110101011⎞⎟ ⎟ ⎟⎠+(𝜆−1)⎛⎜ ⎜ ⎜⎝001010100⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝11𝜆−11𝜆−11𝜆−111⎞⎟ ⎟ ⎟⎠. Como la matriz 𝑀 es cuadrada, rang⁡(𝑀) <3 ⇔|𝑀| =0. Calculamos el determinante de 𝑀. |𝑀|=∣11𝜆−11𝜆−11𝜆−111∣=3(𝜆−1)−(𝜆−1)3−2=3𝜆−5−(𝜆3−3𝜆2+3𝜆−1)=−𝜆3+3𝜆2−4. Si factorizamos el polinomio, obtenemos que |𝑀|=−(𝜆−2)2(𝜆+1). Así que |𝑀|=0⇔−(𝜆−2)2(𝜆+1)=0⇔{𝜆−2=0⇔𝜆=2,𝜆+1=0⇔𝜆=−1. Por tanto, la matriz 𝑀 tiene rango menor que 3 para 𝜆 = −1 y 𝜆 =2.
  2. Si 𝜆 = −1, 𝑀=⎛⎜ ⎜ ⎜⎝11−21−21−211⎞⎟ ⎟ ⎟⎠. Por el apartado anterior sabemos que rang⁡(𝑀) <3. Observamos que ∣111−2∣=−3≠0⇒rang⁡(𝑀)=2. El sistema a resolver es ⎛⎜ ⎜ ⎜⎝11−21−21−211⎞⎟ ⎟ ⎟⎠⎛⎜ ⎜ ⎜⎝𝑥𝑦𝑧⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝000⎞⎟ ⎟ ⎟⎠→⎧{ {⎨{ {⎩𝑥+𝑦−2𝑧=0,𝑥−2𝑦+𝑧=0,−2𝑥+𝑦+𝑧=0. Podemos ver que se trata de un sistema compatible indeterminado por el teorema de Rouché-Frobenius. Como el rango de 𝑀 es 2, el sistema se puede reducir a {𝑥+𝑦−2𝑧=0,𝑥−2𝑦+𝑧=0. Resolvemos el sistema por el método de Gauss. (11−201−210)𝐹2−𝐹1←←←←←←←←→(11−200−330). El sistema resultante es {𝑥+𝑦−2𝑧=0,−3𝑦+3𝑧=0. Si tomamos 𝑧 =𝜇, −3𝑦+3𝑧=0𝑧=𝜇←←←←←←→−3𝑦+3𝜇=0⇔𝑦=𝜇,𝑥+𝑦−2𝑧=0𝑦=𝜇←←←←←←→𝑧=𝜇𝑥+𝜇−2𝜇=0⇔𝑥=𝜇. Por tanto, la solución del sistema es ⎧{ {⎨{ {⎩𝑥=𝜇,𝑦=𝜇,𝑧=𝜇,𝜇∈ℝ.

Ejercicio 7

Considera el plano 𝜋, determinado por los puntos 𝐴( −1,0,0), 𝐵(0,1,1) y 𝐶(2,1,0), y la recta 𝑟≡{𝑥−2𝑧−3=0,𝑦−𝑧−2=0. Halla los puntos de 𝑟 cuya distancia a 𝜋 es √14 unidades.

Resolución

En primer lugar, hallamos las ecuaciones paramétricas de la recta 𝑟. Su vector director viene dado por el producto vectorial: ⃗𝑑=(1,0,−2)×(0,1,−1)=∣⃗𝑥⃗𝑦⃗𝑧10−201−1∣=(2,1,1). Como el punto (3,2,0) pertenece a la recta 𝑟, sus ecuaciones paramétricas son: 𝑟≡⎧{ {⎨{ {⎩𝑥=3+2𝜆,𝑦=2+𝜆,𝑧=𝜆,𝜆∈ℝ.

El plano 𝜋 determinado por los puntos 𝐴, 𝐵 y 𝐶 tiene como vectores directores ⃗𝐴𝐵 =(1,1,1) y ⃗𝐴𝐶 =(3,1,0). El vector normal del plano es perpendicular a ambos, así que: ⃗𝑛=⃗𝐴𝐵×⃗𝐴𝐶=∣⃗𝑥⃗𝑦⃗𝑧111310∣=(−1,3,−2)∥(1,−3,2). Como 𝐴 pertenece al plano, la ecuación de 𝜋 es: 𝜋≡𝑥+1−3𝑦+2𝑧=0⇔𝑥−3𝑦+2𝑧+1=0.

La distancia entre 𝜋 y un punto genérico 𝑅(3 +2𝜆,2 +𝜆,𝜆) de la recta 𝑟 viene dada por: dist⁡(𝑅,𝜋)=|3+2𝜆−3(2+𝜆)+2𝜆+1||⃗𝑛|=|𝜆−2|√12+32+22=|𝜆−2|√14. Como queremos hallar los puntos de 𝑟 cuya distancia a 𝜋 sea de √14 unidades, dist⁡(𝑅,𝜋)=√14⇔|𝜆−2|√14=√14⇔|𝜆−2|=14⇔{𝜆−2=14⇔𝜆=16⇒𝑅1(35,18,16),𝜆−2=−14⇔𝜆=−12⇒𝑅2(−21,−10,−12). Por tanto, los puntos son 𝑅1(35,18,16) y 𝑅2( −21, −10, −12).

Ejercicio 8

Considera el paralelogramo cuyos vértices consecutivos son los puntos 𝑃( −1,2,3), 𝑄( −2,1,0), 𝑅(0,5,1) y 𝑆.

  1. Halla las coordenadas del punto 𝑆.
  2. Calcula la ecuación de la recta que pasa por el origen de coordenadas y es perpendicular al plano que contiene a los puntos 𝑃, 𝑄 y 𝑅.

Resolución
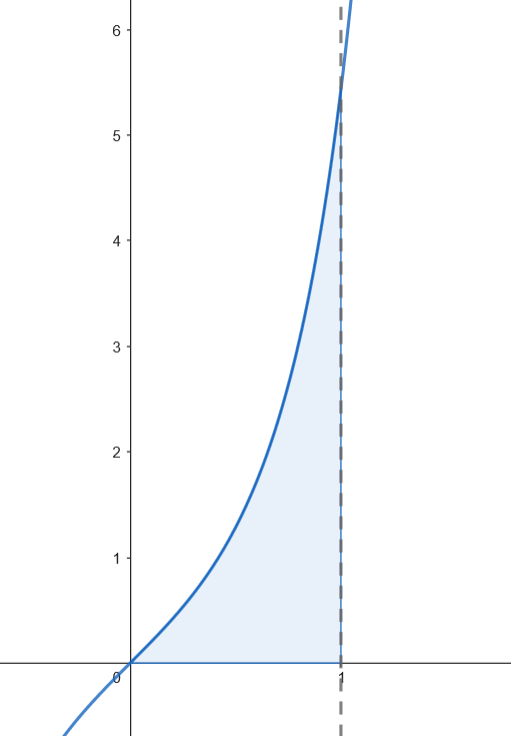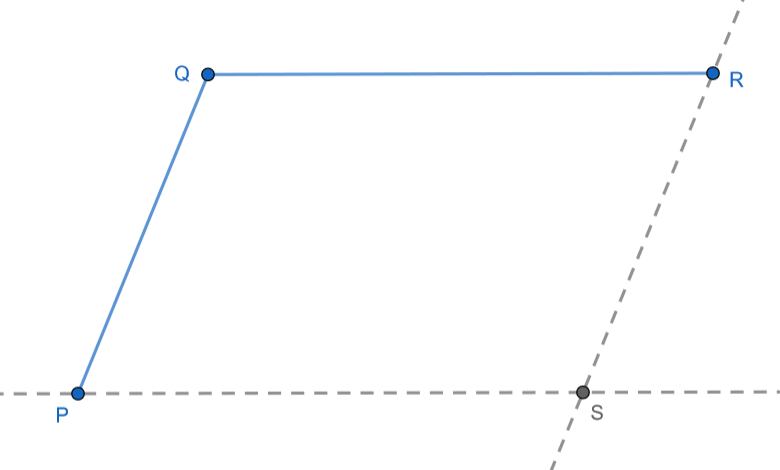  1. Representamos el paralelogramo. Figura Hallamos el punto 𝑆 como intersección de la recta 𝑟 que pasa por 𝑃 con vector director ⃗𝑄𝑅 =(2,4,1) y la recta 𝑠 que pasa por 𝑅 con vector director ⃗𝑃𝑄 =( −1, −1, −3)||(1,1,3), de ecuaciones 𝑟≡⎧{ {⎨{ {⎩𝑥=−1+2𝜆,𝑦=2+4𝜆,𝑧=3+𝜆y𝑠≡⎧{ {⎨{ {⎩𝑥=𝜇,𝑦=5+𝜇,𝑧=1+3𝜇. Calculamos el punto de intersección. ⎧{ {⎨{ {⎩−1+2𝜆=𝜇,2+4𝜆=5+𝜇,3+𝜆=1+3𝜇. Para obtener los valores de 𝜆 y 𝜇, podemos plantear el sistema formado por las dos primeras ecuaciones. {−1+2𝜆=𝜇,2+4𝜆=5+𝜇⇔{2𝜆−𝜇=1,4𝜆−𝜇=3. Resolvemos este sistema por reducción. Si restamos las dos ecuaciones, obtenemos −2𝜆=−2⇔𝜆=1. Por tanto, 𝑆(1,6,4).
  2. El plano determinado por los puntos 𝑃, 𝑄 y 𝑅 tiene como vectores directores ⃗𝑃𝑄=(−1,−1,−3)||(1,1,3)y⃗𝑃𝑅=(1,3,−2). El vector normal al plano es perpendicular a ambos, así que ⃗𝑛=(1,1,3)×(1,3,−2)=∣⃗𝑥⃗𝑦⃗𝑧11313−2∣=(−11,5,2). Si una recta 𝑡 es perpendicular al plano, su vector director es ⃗𝑛. Si además pasa por el origen 𝑂(0,0,0), su ecuación es 𝑡≡⎧{ {⎨{ {⎩𝑥=−11𝜂,𝑦=5𝜂,𝑧=2𝜂.