Ejercicio 6: Junio de 2025
Halla la función
Halla la función
Sea la función
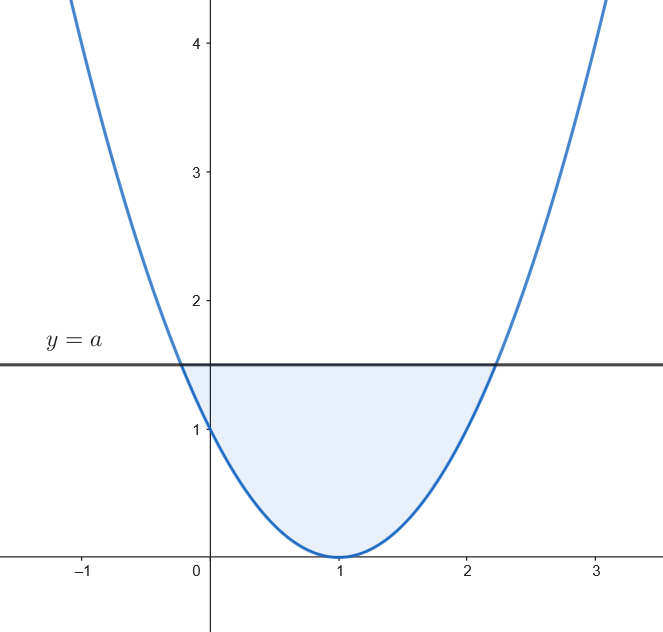
Considera la función
En primer lugar, hallamos una primitiva de la primera rama integrando por partes.
Calculamos la integral definida.
Calcula
Sean las funciones
Sea
Considera las funciones
Considera la función
Calcula el valor de
Considera la función
Halla la función
Como
De igual forma,
Si la gráfica de
De igual forma, si la gráfica pasa por el punto
Así que la función es
Considera la función
Calcula
Considera la función
Calcula una primitiva de la función
Considera la función
Calcula
Halla la función
Sea
Sean
Halla
Considera la función
Considera la función
Calcula
Considera la función
Sabiendo que
Considera la función
Determina la función
Considera las funciones
Calcula una primitiva de la función
Considera la función
Calcula
Considera las funciones
Sea
Considera la función
Considera la función
Considera las funciones
Considera la función
Calcula
Considera la función
Calcula
Calcula
Considera las funciones
Calcula
Considera las funciones
Considera la función
Considera la función
Considera la función
Calcula
Considera la función
Considera la función
Considera la función
Calcula
Calcula
Considera las funciones
Considera la función
Considera la función
Calcula
Sea
Sea
Calcula
Determina la función
Considera las funciones
Determina la única función derivable
Calcula el valor de
Considera la función
Calcula
Calcula
Considera las funciones
Sea la función
Considera las funciones
Calcula
Sean las funciones
Sea
Considera las funciones
Dado un número real
Sea
Sea
Considera la función
Determina la función
Sea la función
Considera las funciones
Considera las funciones
Sea
Considera la función
Determina la función
Sea
Siendo
Calcula
Considera las funciones
Se sabe que la función
Considera la función
Considera la función
Considera la región limitada por las curvas
Calcula
Considera la función dada por
Sea
Sea
Sea
Considera la región limitada por la gráfica de la función dada por
Calcula
Calcula
Determina la función
Considera el recinto del primer cuadrante limitado por el eje
Halla la ecuación de la recta tangente a la gráfica de una función
Sea
Considera la función
Sea
De la función
Considera la función
Calcula el valor de
Considera la función
Calcula
Determina la función
Sea
Calcula
Calcula
Determina la función
Calcula
Sea
Sea
Calcula
Sea
Sea
Calcula el valor de
Sea
Calcula
Sea
Sean
Sea
Determina una función derivable
Considera el recinto limitado por las siguientes curvas:
Calcula
Sea
Sea
Sea
Calcula
Sea
Calcula
Calcula
Sean
Sea
De la función
Calcula
Halla
Sea
Sea
Calcula
Sean
Calcula
Sea
Sea
Sea la función
Sean
Sea la función
Sea
Sean
Se considera el recinto del plano situado en el primer cuadrante limitado por las rectas
Calcula los valores de
Sea la función
Sean las funciones
Sea
Sea
Sea
Halla:
Determina la función
Calcula:
Calcula el valor de
Sea
Sean
Calcula:
Calcula un número positivo
Dada la función
Considera las funciones
Sean
Calcula
Considera la función
Sea
Considera la función