Matemáticas de Selectividad

1. En primer lugar, calculamos la derivada de 𝑓. 𝑓′(𝑥)={5,si −2≤𝑥<0,𝑒𝑥(cos⁡(𝑥)−sen⁡(𝑥)),si 0<𝑥≤2𝜋. Para hallar los puntos críticos, igualamos las dos ramas de la derivada de 𝑓 a cero.
   • Si −2 ≤𝑥 <0, 𝑓′(𝑥) =5 ≠0.
   • Si 0 <𝑥 ≤2𝜋, 𝑓′(𝑥)=0⇔𝑒𝑥(cos⁡(𝑥)−sen⁡(𝑥))=0⇔cos⁡(𝑥)−sen⁡(𝑥)=0⇔cos⁡(𝑥)=sen⁡(𝑥)⇔{𝑥=𝜋4,𝑥=5𝜋4.
   Así que los puntos críticos son 𝑥 =𝜋4 y 𝑥 =5𝜋4. También consideraremos 𝑥 =0 por ser el punto de ruptura. Estudiamos el signo de la derivada para determinar si se tratan de extremos.

   	( −2,0)	(0,𝜋4)	(𝜋4,5𝜋4)	(5𝜋4,2𝜋)
   signo de 𝑓′	+	+	−	+
   monotonía de 𝑓	→	→	→	→

   Por tanto, considerando también los extremos del intervalo, 𝑓 tiene máximos relativos en 𝑥 =𝜋4 y 𝑥 =2𝜋 y tiene mínimos relativos en 𝑥 = −2 y 𝑥 =5𝜋4. Es decir, los puntos (𝜋4,𝑒𝜋4√22) y (2𝜋,𝑒2𝜋) son máximos relativos y los puntos ( −2, −9) y (5𝜋4,−𝑒5𝜋4√22) son mínimos relativos. Comparando, podemos concluir que el punto (2𝜋,𝑒2𝜋) es un máximo absoluto y el punto (5𝜋4,−𝑒5𝜋4√22) es un mínimo absoluto.
2. La ecuación de la recta tangente a la gráfica de 𝑓 en 𝑥 =𝜋2 es 𝑦−𝑓(𝜋2)=𝑓′(𝜋2)(𝑥−𝜋2)→𝑦=−𝑒𝜋2(𝑥−𝜋2)⇔𝑦=−𝑒𝜋2𝑥+𝑒𝜋2𝜋2.

1. En primer lugar, calculamos la derivada de 𝑓. 𝑓′(𝑥)=ln2⁡(𝑥)+2ln⁡(𝑥)=ln⁡(𝑥)(ln⁡(𝑥)+2). Para hallar los puntos críticos, igualamos la derivada de 𝑓 a cero. 𝑓′(𝑥)=0⇔ln⁡(𝑥)(ln⁡(𝑥)+2)=0⇔{ln⁡(𝑥)=0⇔𝑥=1,ln⁡(𝑥)+2=0⇔ln⁡(𝑥)=−2⇔𝑥=𝑒−2. Así que los puntos críticos son 𝑥 =𝑒−2 y 𝑥 =1. Estudiamos el signo de la derivada para determinar si se tratan de extremos.

   	(0,𝑒−2)	(𝑒−2,1)	(1, +∞)
   signo de 𝑓′	+	−	+
   monotonía de 𝑓	→	→	→

   Por tanto, 𝑓 tiene un máximo relativo en 𝑥 =𝑒−2 y un mínimo relativo en 𝑥 =1. Es decir, el punto (𝑒−2,4𝑒−2) es un máximo relativo y el punto (1,0) es un mínimo relativo.
2. Veamos si alguno de los extremos relativos de 𝑓 es absoluto. Por un lado, observamos que lím𝑥→0+⁡𝑓(𝑥)=lím𝑥→0+⁡𝑥ln2⁡(𝑥)=0, así que 𝑓 no alcanza valores inferiores a 0. Por tanto, (1,0) es un mínimo absoluto. Por otro lado, como lím𝑥→+∞⁡𝑓(𝑥)=lím𝑥→+∞⁡𝑥ln2⁡(𝑥)=+∞, entonces 𝑓 no tiene ningún máximo absoluto.

En primer lugar, hallamos una primitiva de la función 𝑓(𝑥)=ln⁡(𝑥)𝑥=1𝑥ln⁡(𝑥).

Como 1𝑥 es la derivada de ln⁡(𝑥), ∫1𝑥ln⁡(𝑥)=12ln2⁡(𝑥).

Calculamos la integral definida. ∫1𝑎ln⁡(𝑥)𝑥𝑑𝑥=12[ln2⁡(𝑥)]1𝑎=−12ln2⁡(𝑎).

Por tanto, ∫1𝑎ln⁡(𝑥)𝑥𝑑𝑥+2=0⇔−12ln2⁡(𝑎)+2=0⇔ln2⁡(𝑎)=4. Como 0 <𝑎 <1, entonces ln⁡(𝑎) <0. Así que ln2⁡(𝑎)=4⇒ln⁡(𝑎)=−2⇔𝑎=𝑒−2.

1. Calculamos los puntos de corte de las dos funciones. 𝑓(𝑥)=𝑔(𝑥)⇔5−𝑥2=4𝑥2⇔−𝑥4+5𝑥2−4=0. Para resolver esta ecuación bicuadrada, hacemos el cambio de variable 𝑡 =𝑥2. De esta forma, −𝑥4+5𝑥2−4=0⇔−𝑡2+5𝑡−4=0⇔{𝑡=1⇔𝑥2=1⇔𝑥=±1,𝑡=4⇔𝑥2=4⇔𝑥=±2. Por tanto, los puntos de corte son ( −2,1), ( −1,4), (1,4) y (2,1).
   Representamos gráficamente las dos funciones. Observamos que ambas funciones tienen simetría par y la parábola tiene vértice (0,5).
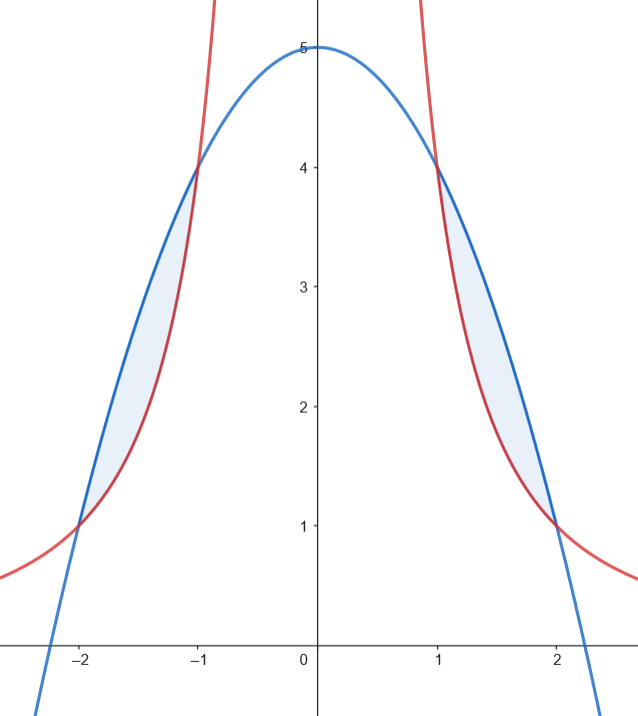2. Podemos representar los recintos limitados por las gráficas de 𝑓 y 𝑔. Como los dos recintos tienen la misma superficie, podemos calcular el área como 2∫21(𝑓(𝑥)−𝑔(𝑥))𝑑𝑥=2∫21(5−𝑥2−4𝑥2)𝑑𝑥=2[5𝑥−13𝑥3+4𝑥]21==2[10−83+2−(5−13+4)]=43𝑢2.

1. Calculamos en primer lugar el determinante de la matriz 𝐴 −𝑚𝐼. |𝐴−𝑚𝐼|=∣1−𝑚1111−𝑚1111−𝑚∣=(1−𝑚)3+2−3(1−𝑚)=−𝑚3+3𝑚2. La matriz 𝐴 −𝑚𝐼 no tiene inversa si y solo si su determinante es nulo. |𝐴−𝑚𝐼|=0⇔−𝑚3+3𝑚2=0⇔𝑚2(𝑚−3)=0⇔{𝑚=0,𝑚=3. Por tanto, la matriz 𝐴 −𝑚𝐼 no tiene inversa si 𝑚 =0 o 𝑚 =3.
2. En primer lugar, hallamos la inversa de la matriz 1𝑥(𝐴 −𝐼). (1𝑥(𝐴−𝐼))−1=𝑥(𝐴−𝐼)−1. La matriz 𝐴 −𝐼 es de la forma 𝐴 −𝑚𝐼 con 𝑚 =1, así que por el apartado anterior es invertible y det(𝐴 −𝐼) =2. Para hallar su inversa, calculamos primero su matriz adjunta. Adj⁡(𝐴−𝐼)=⎛⎜ ⎜ ⎜⎝−1111−1111−1⎞⎟ ⎟ ⎟⎠. Ahora podemos calcular la inversa como (𝐴−𝐼)−1=1|𝐴−𝐼|Adj⁡(𝐴)𝑡=12⎛⎜ ⎜ ⎜⎝−1111−1111−1⎞⎟ ⎟ ⎟⎠. Así que (1𝑥(𝐴−𝐼))−1=𝑥2⎛⎜ ⎜ ⎜⎝−1111−1111−1⎞⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜ ⎜⎝−𝑥2𝑥2𝑥2𝑥2−𝑥2𝑥2𝑥2𝑥2−𝑥2⎞⎟ ⎟ ⎟ ⎟⎠. Para que 𝐴 −𝑥𝐼 sea la inversa de la matriz 1𝑥(𝐴 −𝐼), ha de ocurrir que (1𝑥(𝐴−𝐼))−1=𝐴−𝑥𝐼⇔⎛⎜ ⎜ ⎜ ⎜⎝−𝑥2𝑥2𝑥2𝑥2−𝑥2𝑥2𝑥2𝑥2−𝑥2⎞⎟ ⎟ ⎟ ⎟⎠=⎛⎜ ⎜ ⎜⎝1−𝑥1111−𝑥1111−𝑥⎞⎟ ⎟ ⎟⎠⇔⎧{ {⎨{ {⎩−𝑥2=1−𝑥,𝑥2=1⇔𝑥=2.

Llamamos 𝑥 al importe sin impuestos de refrescos, 𝑦 al de cerveza y 𝑧 al de vino.

En primer lugar, si el importe total sin impuestos es de 500€, entonces 𝑥+𝑦+𝑧=500.

Además, si el gasto en vino es de 60€ menos que los gastos en refrescos y cerveza conjuntamente y sin impuestos, 𝑧=𝑥+𝑦−60.

Por último, si los impuestos son del 6%, 12% y 30% respectivamente y el importe total con impuestos es de 592,4€, 1,06𝑥+1,12𝑦+1,3𝑧=592,4.

Por tanto, podemos plantear el sistema de ecuaciones lineales ⎧{ {⎨{ {⎩𝑥+𝑦+𝑧=500,𝑧=𝑥+𝑦−60,1,06𝑥+1,12𝑦+1,3𝑧=592,4⇒⎧{ {⎨{ {⎩𝑥+𝑦+𝑧=500,𝑥+𝑦−𝑧=60,106𝑥+112𝑦+130𝑧=59240.

Resolvemos el sistema mediante el método de Gauss. ⎛⎜ ⎜ ⎜ ⎜⎝11150011−16010611213059240⎞⎟ ⎟ ⎟ ⎟⎠𝐹1−𝐹2←←←←←←←←←←←←←←→𝐹3−106𝐹2⎛⎜ ⎜ ⎜ ⎜⎝00244011−1600623652880⎞⎟ ⎟ ⎟ ⎟⎠ El sistema resultante es ⎧{ {⎨{ {⎩2𝑧=440,𝑥+𝑦−𝑧=60,6𝑦+236𝑧=52880⇒⎧{ {⎨{ {⎩𝑧=220,𝑥+𝑦−𝑧=60,3𝑦+118𝑧=26440.

Por tanto, 𝑧=220,3𝑦+118𝑧=26440𝑧=220←←←←←←←←←→3𝑦+25960=26440⇔3𝑦=480⇔𝑦=160,𝑥+𝑦−𝑧=60𝑦=160←←←←←←←←←→𝑧=220𝑥+160−220=60⇔𝑥=120. Así que el importe de cada una de las bebidas con impuestos es

• Refrescos: 1,06 ⋅120 =127,20€.
• Cerveza: 1,12 ⋅160 =179,20€.
• Vino: 1,3 ⋅220 =286€.

1. La recta 𝑟 intersección de los planos 𝜋1 y 𝜋2 viene dada por 𝑟≡{𝑥−𝑦+𝑧=0,𝑥+𝑦=2. Hallamos en primer lugar las ecuaciones paramétricas de 𝑟. Su vector director viene dado por el producto vectorial de los vectores normales de cada plano, ⃗𝑛1 =(1, −1,1) y ⃗𝑛2 =(1,1,0). ⃗𝑑𝑟=⃗𝑛1×⃗𝑛2=∣⃗𝑥⃗𝑦⃗𝑧1−11110∣=(−1,1,2). Como el punto (0,2,2) pertenece a la recta 𝑟, sus ecuaciones paramétricas son 𝑟≡⎧{ {⎨{ {⎩𝑥=−𝜆,𝑦=2+𝜆,𝑧=2+2𝜆. Para hallar la distancia de la recta 𝑟 al punto 𝑃 podemos trazar un plano 𝜏 perpendicular a 𝑟 que pase por 𝑃. Este plano cortará a 𝑟 en un punto 𝑄, de forma que dist⁡(𝑃,𝑟) =dist⁡(𝑃,𝑄). Si 𝜏 es perpendicular a 𝑟, su vector normal es ⃗𝑛 =⃗𝑑𝑟 =( −1,1,2). Así que la ecuación del plano 𝜏 es 𝜏≡−(𝑥−2)+𝑦−6+2(𝑧+2)=0⇔−𝑥+𝑦+2𝑧=0. Calculamos el punto 𝑄 =𝑟 ∩𝜏. Para ello sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. −(−𝜆)+2+𝜆+2(2+2𝜆)=0⇔6𝜆=−6⇔𝜆=−1. Por tanto, el punto de corte es 𝑄(1,1,0).
   Por último, calculamos la distancia de 𝑃 a 𝑟 como el módulo del vector ⃗𝑃𝑄 =( −1, −5,2). dist⁡(𝑃,𝑟)=dist⁡(𝑃,𝑄)=|⃗𝑃𝑄|=√1+52+22=√30𝑢.
2. El coseno del ángulo 𝛼 que forman los planos 𝜋1 y 𝜋2 viene dado por cos⁡(𝛼)=⃗𝑛1⋅⃗𝑛2|⃗𝑛1||⃗𝑛2|=0. Por tanto, el ángulo que forman es de 90º.

El plano 𝜋 determinado por los puntos 𝐴, 𝐵 y 𝐶 tiene como vectores directores ⃗𝐴𝐵=(3,0,3)∥(1,0,1)𝑦⃗𝐴𝐶=(2,1,4). El vector normal al plano es perpendicular a ambos, así que ⃗𝑛=(1,0,1)×(2,1,4)=∣⃗𝑥⃗𝑦⃗𝑧101214∣=(−1,−2,1). Como 𝐴 pertenece al plano, la ecuación de 𝜋 es 𝜋≡−𝑥−2(𝑦−2)+𝑧+2=0⇔−𝑥−2𝑦+𝑧+6=0.

Hallamos los puntos de corte de 𝜋 con los ejes de coordenadas.

• El eje 𝑋 tiene de ecuaciones 𝑦 =0 y 𝑧 =0. Sustituyendo en la ecuación del plano, −𝑥+6=0⇔𝑥=6. Por tanto, el punto de corte es 𝐷(6,0,0).
• El eje 𝑌 tiene de ecuaciones 𝑥 =0 y 𝑧 =0. Sustituyendo en la ecuación del plano, −2𝑦+6=0⇔𝑦=3. Por tanto, el punto de corte es 𝐸(0,3,0).
• El eje 𝑍 tiene de ecuaciones 𝑥 =0 e 𝑦 =0. Sustituyendo en la ecuación del plano, 𝑧+6=0⇔𝑧=−6. Por tanto, el punto de corte es 𝐹(0,0, −6).

El volumen del tetraedro delimitado por el plano 𝜋 y los planos cartesianos es un sexto del volumen del paralelepípedo formado por los vectores ⃗𝑂𝐷 =(6,0,0), ⃗𝑂𝐸 =(0,3,0) y ⃗𝑂𝐹 =(0,0, −6). Este viene dado por el valor absoluto del producto mixto de los tres vectores. [⃗𝑂𝐷,⃗𝑂𝐸,⃗𝑂𝐹]=∣60003000−6∣=−108⇒𝑉=108𝑢3. Por tanto, el volumen del tetraedro es 16 ⋅108 =18 𝑢3.