Matemáticas de Selectividad

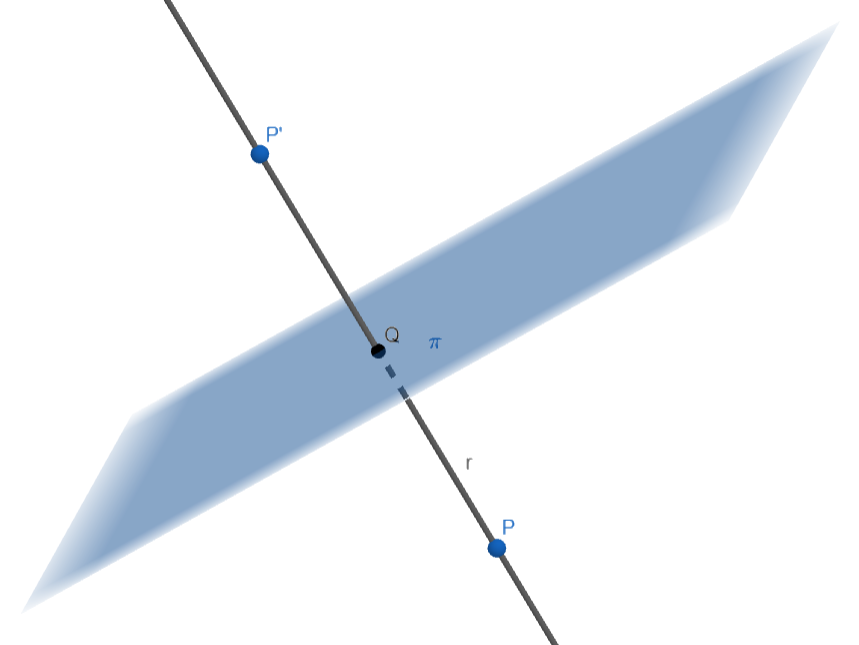
1. Para hallar el punto simétrico 𝑃′ de 𝑃 con respecto a 𝜋, trazamos una recta 𝑟 perpendicular al plano que pase por el punto 𝑃. Al ser perpendicular a 𝜋, su vector director es ⃗𝑑𝑟 =⃗𝑛𝜋 =(2,1,2). Así que la ecuación de la recta 𝑟 es: 𝑟≡⎧{ {⎨{ {⎩𝑥=1+2𝜆,𝑦=𝜆,𝑧=1+2𝜆,𝜆∈ℝ. A continuación, hallamos el punto de intersección 𝑄 entre la recta y el plano sustituyendo las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 2(1+2𝜆)+𝜆+2(1+2𝜆)+5=0⇔2+4𝜆+𝜆+2+4𝜆+5=0⇔9𝜆+9=0⇔𝜆=−1. Por tanto, el punto de intersección es 𝑄( −1, −1, −1). De esta forma, podemos hallar 𝑃′ como el punto simétrico de 𝑃 con respecto a 𝑄. Si llamamos 𝑃′(𝑎,𝑏,𝑐), ha de verificarse: ⎧{ {⎨{ {⎩1+𝑎2=−1⇔𝑎=−3,𝑏2=−1⇔𝑏=−2,1+𝑐2=−1⇔𝑐=−3. Por tanto, el punto simétrico de 𝑃 con respecto al plano 𝜋 es 𝑃′( −3, −2, −3).
2. Llamamos 𝜏 al plano que nos piden. Como 𝜏 es un plano paralelo a 𝜋, su vector normal es ⃗𝑛𝜏 =⃗𝑛𝜋 =(2,1,2). Así que la ecuación del plano 𝜏 es de la forma: 𝜏≡2𝑥+𝑦+2𝑧+𝑑=0. El punto 𝑄( −1, −1, −1) pertenece al plano 𝜋, así que la distancia entre 𝜋 y 𝜏 viene dada por: dist⁡(𝜋,𝜏)=dist⁡(𝑄,𝜏)=|2⋅(−1)+(−1)+2⋅(−1)+𝑑|√22+12+22=|−5+𝑑|3. Para que la distancia sea de 2 unidades, ha de verificarse: dist⁡(𝜋,𝜏)=2⇔|−5+𝑑|3=2⇔|−5+𝑑|=6⇔{−5+𝑑=6⇔𝑑=11,−5+𝑑=−6⇔𝑑=−1. Por tanto, las ecuaciones de los planos son: 𝜏1≡2𝑥+𝑦+2𝑧+11=0y𝜏2≡2𝑥+𝑦+2𝑧−1=0.

1. En primer lugar, hallamos las ecuaciones paramétricas de la recta 𝑟. Si tomamos 𝑦 =𝜆, entonces 𝑦−𝑧=1⇔𝑧=−1+𝑦𝑦=𝜆←←←←←←←→𝑧=−1+𝜆,𝑥−2𝑦+𝑧=2⇔𝑥=2+2𝑦−𝑧𝑦=𝜆←←←←←←←←←←←←→𝑧=−1+𝜆𝑥=2+2𝜆+1−𝜆=3+𝜆. Luego las ecuaciones paramétricas de 𝑟 son 𝑟≡⎧{ {⎨{ {⎩𝑥=3+𝜆,𝑦=𝜆,𝑧=−1+𝜆. Para hallar el punto simétrico 𝑃′ de 𝑃 con respecto a 𝑟, trazamos un plano 𝜏 perpendicular a la recta que pase por el punto 𝑃. Al ser perpendicular a 𝑟, su vector normal es ⃗𝑛𝜏 =⃗𝑑𝑟 =(1,1,1). Así que la ecuación del plano 𝜏 es 𝜏≡𝑥−2+𝑦−2+𝑧−1=0⇔𝑥+𝑦+𝑧−5=0. A continuación, hallamos el punto de intersección 𝑅 de la recta 𝑟 y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 3+𝜆+𝜆−1+𝜆−5=0⇔3𝜆−3=0⇔𝜆=1. Por tanto, el punto de intersección es 𝑅(4,1,0). Como 𝑅 es el punto medio de 𝑃 y 𝑃′, podemos hallar 𝑃′ como el simétrico de 𝑃 respecto de 𝑅. Si llamamos 𝑃′(𝑎,𝑏,𝑐), tiene que verificarse: ⎧{ {⎨{ {⎩2+𝑎2=4⇔𝑎=6,2+𝑏2=1⇔𝑏=0,1+𝑐2=0⇔𝑐=−1. Por tanto, el punto simétrico de 𝑃 con respecto a la recta 𝑟 es 𝑃′(6,0, −1).
2. Para hallar el punto simétrico 𝑄′ de 𝑄 con respecto a 𝜋, trazamos una recta 𝑠 perpendicular al plano que pase por el punto 𝑄. Al ser perpendicular a 𝜋, su vector director es ⃗𝑑𝑠 =⃗𝑛𝜋 =(1, −2,1). Así que las ecuaciones de la recta 𝑠 son 𝑠≡⎧{ {⎨{ {⎩𝑥=1+𝜇,𝑦=−1−2𝜇,𝑧=−3+𝜇. A continuación, hallamos el punto de intersección 𝑆 de la recta 𝑠 y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑠 en la ecuación del plano. 1+𝜇−2(−1−2𝜇)−3+𝜇+6=0⇔6𝜇+6=0⇔𝜇=−1. Por tanto, el punto de intersección es 𝑆(0,1, −4). Como 𝑆 es el punto medio de 𝑄 y 𝑄′, podemos hallar 𝑄′ como el simétrico de 𝑄 respecto de 𝑆. Si llamamos 𝑄′(𝑎,𝑏,𝑐), tiene que verificarse: ⎧{ {⎨{ {⎩1+𝑎2=0⇔𝑎=−1,−1+𝑏2=1⇔𝑏=3,−3+𝑐2=−4⇔𝑐=−5. Por tanto, el punto simétrico de 𝑄 con respecto al plano 𝜋 es 𝑄′( −1,3, −5).

En primer lugar, el plano 𝜋 determinado por los puntos 𝐵, 𝐶 y 𝐷 tiene como vectores directores ⃗𝐵𝐶=(−1,−23,−1)∥(3,2,3)y⃗𝐵𝐷=(−4,−1,1). El vector normal al plano es perpendicular a ambos, así que ⃗𝑛=(3,2,3)×(−4,−1,1)=∣⃗𝑥⃗𝑦⃗𝑧323−4−11∣=(5,−15,5)∥(1,−3,1). Como 𝐵 pertenece al plano, la ecuación de 𝜋 es 𝜋≡𝑥−1−3(𝑦−1)+𝑧−2=0⇔𝑥−3𝑦+𝑧=0.

Para hallar el punto simétrico 𝐴′ de 𝐴 con respecto a 𝜋, trazamos una recta 𝑟 perpendicular al plano que pase por el punto 𝐴. Al ser perpendicular a 𝜋, su vector director es ⃗𝑑 =⃗𝑛 =(1, −3,1). Así que la ecuación de la recta 𝑟 es 𝑟≡⎧{ {⎨{ {⎩𝑥=2+𝜆,𝑦=−4−3𝜆,𝑧=−3+𝜆. A continuación, hallamos el punto de intersección 𝑀 de la recta y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 2+𝜆−3(−4−3𝜆)−3+𝜆=0⇔11𝜆+11=0⇔𝜆=−1. Por tanto, el punto de corte es 𝑀(1, −1, −4).

Como 𝑀 es el punto medio de 𝐴 y 𝐴′, podemos hallar 𝐴′ como el simétrico de 𝐴 respecto de 𝑀. Si llamamos 𝐴′(𝑎,𝑏,𝑐), tiene que verificarse ⎧{ { { {⎨{ { { {⎩2+𝑎2=1⇔2+𝑎=2⇔𝑎=0,−4+𝑏2=−1⇔−4+𝑏=−2⇔𝑏=2,−3+𝑐2=−4⇔−3+𝑐=−8⇔𝑐=−5. Por tanto, el punto simétrico de 𝐴 con respecto al plano 𝜋 es 𝐴′(0,2, −5).

1. En primer lugar, hallamos la ecuación general del plano 𝜋. Su vector normal viene dado por el producto vectorial ⃗𝑛=(9,2,4)×(3,0,1)=∣⃗𝑥⃗𝑦⃗𝑧924301∣=(2,3,−6). Como el punto (0, −1,3) pertenece al plano 𝜋, su ecuación general es 𝜋≡2𝑥+3(𝑦+1)−6(𝑦−3)=0⇔2𝑥+3𝑦−6𝑧+21=0. Para hallar el punto simétrico 𝑃′ de 𝑃 con respecto a 𝜋, trazamos una recta 𝑟 perpendicular al plano que pase por el punto 𝑃. Al ser perpendicular a 𝜋, el vector director de la recta es ⃗𝑛 =(2,3, −6). Así que la ecuación de la recta 𝑟 es 𝑟≡⎧{ {⎨{ {⎩𝑥=2+2𝜆,𝑦=3𝜆,𝑧=−4−6𝜆. A continuación, hallamos el punto de intersección 𝑄 de la recta y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 2(2+𝜆)+3⋅3𝜆−6(−4−6𝜆)+21=0⇔49𝜆+49=0⇔𝜆=−1. Por tanto, el punto de corte es 𝑄(0, −3,2). Como 𝑄 es el punto medio de 𝑃 y 𝑃′, podemos hallar 𝑃′ como el simétrico de 𝑃 con respecto a 𝑄. Si llamamos 𝑃′(𝑎,𝑏,𝑐), tiene que verificarse ⎧{ {⎨{ {⎩2+𝑎2=0⇔𝑎=−2,0+𝑏2=−3⇔𝑏=−6,−4+𝑐2=2⇔𝑐=8. Por tanto, el punto simétrico de 𝑃 con respecto al plano 𝜋 es 𝑃′( −2, −6,8).
2. Por el apartado anterior, dist⁡(𝑃,𝜋) =dist⁡(𝑃,𝑄). Calculamos la distancia de 𝑃 a 𝜋 como el módulo del vector ⃗𝑃𝑄 =( −2, −3,6). dist⁡(𝑃,𝜋)=dist⁡(𝑃,𝑄)=|⃗𝑃𝑄|=√22+32+62=√49=7𝑢.

1. En primer lugar hallamos las ecuaciones paramétricas de la recta 𝑟. Como su vector director es ⃗𝑑𝑟 =(1,3,1) y pasa por el punto (0,0,1), 𝑟≡⎧{ {⎨{ {⎩𝑥=𝜆,𝑦=3𝜆,𝑧=1+𝜆. Para hallar el punto de intersección de 𝑟 y 𝜋, sustituimos las ecuaciones de 𝑟 en la ecuación del plano. 𝜆+3𝜆−(1+𝜆)=2⇔3𝜆=3⇔𝜆=1. Por tanto, el punto de intersección es (1,3,2).
2. Para hallar el punto simétrico 𝑄′ de 𝑄 con respecto a 𝜋 trazamos una recta 𝑠 perpendicular al plano que pase por el punto 𝑄. Al ser perpendicular a 𝜋, su vector director es ⃗𝑑𝑠 =⃗𝑛𝜋 =(1,1, −1). Así que la ecuación de la recta 𝑠 es 𝑠≡⎧{ {⎨{ {⎩𝑥=2+𝜇,𝑦=6+𝜇,𝑧=3−𝜇. A continuación, hallamos el punto de intersección 𝑀 de la recta 𝑠 y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑠 en la ecuación del plano. 2+𝜇+6+𝜇−(3−𝜇)=2⇔3𝜇+5=2⇔𝜇=−1. Por tanto, el punto de corte es 𝑀(1,5,4). Como 𝑀 es el punto medio de 𝑄 y 𝑄′, podemos hallar 𝑄′ como el simétrico de 𝑄 respecto de 𝑀. Si llamamos 𝑄′ =(𝑎,𝑏,𝑐), tiene que verificarse ⎧{ { { {⎨{ { { {⎩2+𝑎2=1⇔2+𝑎=2⇔𝑎=0,6+𝑏2=5⇔6+𝑏=10⇔𝑏=4,3+𝑐2=4⇔3+𝑐=8⇔𝑐=5. Por tanto, el punto simétrico de 𝑄 con respecto al plano 𝜋 es 𝑄′(0,4,5).

1. Llamamos 𝜏 al plano que queremos hallar. Como 𝜏 es un plano paralelo a 𝜋, tiene el mismo vector normal. Luego su ecuación será de la forma 𝜏≡2𝑥−𝑦+𝑧+𝑑=0. El punto 𝐴(0,0,0) pertenece al plano 𝜋, así que la distancia entre 𝜋 y 𝜏 viene dada por dist⁡(𝜋,𝜏)=dist⁡(𝐴,𝜏)=|𝑑||⃗𝑛|=|𝑑|√6. Como queremos que la distancia sea de √6 unidades, dist⁡(𝜋,𝜏)=√6⇔|𝑑|√6=√6⇔|𝑑|=6⇔𝑑=±6. Por tanto, las ecuaciones de los planos son 𝜏1≡2𝑥−𝑦+𝑧+6=0y𝜏2≡2𝑥−𝑦+𝑧−6=0.
2. Para hallar el punto simétrico 𝑃′ de 𝑃 con respecto a 𝜋, trazamos una recta 𝑟 perpendicular al plano que pase por el punto 𝑃. Al ser perpendicular a 𝜋, su vector director es ⃗𝑑 =⃗𝑛 =(2, −1,1). Así que las ecuaciones de la recta 𝑟 son ⎧{ {⎨{ {⎩𝑥=1+2𝜆,𝑦=2−𝜆,𝑧=6+𝜆. A continuación, hallamos el punto de intersección 𝑄 de la recta 𝑟 y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 2(1+2𝜆)−(2−𝜆)+6+𝜆=0⇔2+4𝜆−2+𝜆+6+𝜆=0⇔6𝜆+6=0⇔𝜆=−1. Por tanto, el punto de intersección es 𝑄( −1,3,5). Como 𝑄 es el punto medio de 𝑃 y 𝑃′, podemos hallar 𝑃′ como el simétrico de 𝑃 con respecto a 𝑄. Si llamamos 𝑃′(𝑎,𝑏,𝑐), tiene que verificarse: ⎧{ {⎨{ {⎩1+𝑎2=−1⇔𝑎=−3,2+𝑏2=3⇔𝑏=4,6+𝑐2=5⇔𝑐=4. Por tanto, el punto simétrico de 𝑃 con respecto al plano 𝜋 es 𝑃′( −3,4,4).

1. Para hallar el punto simétrico 𝑃′ de 𝑃 con respecto a 𝜋, trazamos una recta 𝑠 perpendicular al plano que pase por 𝑃. Al ser perpendicular a 𝜋, su vector director es ⃗𝑑𝑠 =⃗𝑛𝜋 =(1, −1,1). Así que las ecuaciones paramétricas de la recta 𝑠 son 𝑠≡⎧{ {⎨{ {⎩𝑥=1+𝜆,𝑦=−𝜆,𝑧=1+𝜆. A continuación, hallamos el punto de intersección 𝑄 de la recta 𝑠 y el plano. Para ello sustituimos las ecuaciones paramétricas de 𝑠 en la ecuación del plano. 1+𝜆−(−𝜆)+1+𝜆+1=0⇔3+3𝜆=0⇔𝜆=−1. Por tanto, el punto de intersección es 𝑄(0,1,0). Como 𝑄 es el punto medio de 𝑃 y 𝑃′, podemos hallar 𝑃′ como el simétrico de 𝑃 con respecto de 𝑄. Si llamamos 𝑃′(𝑎,𝑏,𝑐), tiene que verificase: ⎧{ {⎨{ {⎩1+𝑎2=0⇔𝑎=−1,𝑏2=1⇔𝑏=2,1+𝑐2=0⇔𝑐=−1. Por tanto, el punto simétrico de 𝑃 con respecto al plano 𝜋 es 𝑃′( −1,2, −1).
2. Por el apartado anterior, dist⁡(𝑃,𝜋) =dist⁡(𝑃,𝑄). Calculamos la distancia de 𝑃 a 𝜋 como el módulo del vector ⃗𝑃𝑄 =( −1,1, −1). dist⁡(𝑃,𝜋)=dist⁡(𝑃,𝑄)=|⃗𝑃𝑄|=√12+12+12=√3𝑢.

1. El plano 𝜋 es perpendicular al vector ⃗𝐴𝐵 =(0,−12,12) ∥(0,1, −1), así que el vector normal del plano es ⃗𝑛 =(0,1, −1). Como además pasa por el punto 𝐵(1,12,12), 𝜋≡𝑦−12−(𝑧−12)=0⇔𝑦−𝑧=0.
2. La distancia de 𝐴 a su simétrico 𝐴′ respecto a 𝜋 es el doble de la distancia de 𝐴 al punto 𝐵. Por tanto, dist⁡(𝐴,𝐴′)=2dist⁡(𝐴,𝐵)=2|⃗𝐴𝐵|=2√(12)2+(12)2=2√2=√2𝑢.

En primer lugar, hallamos las ecuaciones paramétricas de la recta 𝑟. Si 𝑧 =𝜆, 𝑥−𝑧=1⇔𝑥=1+𝑧=1+𝜆,𝑥−𝑦+2𝑧=5⇔𝑦=𝑥+2𝑧−5=1+𝜆+2𝜆−5=−4+3𝜆. Por tanto, 𝑟≡⎧{ {⎨{ {⎩𝑥=1+𝜆,𝑦=−4+3𝜆,𝑧=𝜆,𝜆∈ℝ.

1. Para hallar el punto simétrico 𝑃′ de 𝑃 con respecto a 𝑟, trazamos un plano 𝜋 perpendicular a la recta que pase por 𝑃. Al ser perpendicular a 𝑟, su vector normal es ⃗𝑛𝜋 =⃗𝑑𝑟 =(1,3,1). Así que la ecuación del plano 𝜋 es: 𝜋≡𝑥−1+3𝑦+𝑧+1=0⇔𝑥+3𝑦+𝑧=0. A continuación, hallamos el punto de intersección 𝑄 de la recta 𝑟 y el plano. Para ello, sustituimos las ecuaciones paramétricas de 𝑟 en la ecuación del plano. 1+𝜆+3(−4+3𝜆)+𝜆=0⇔1+𝜆−12+9𝜆+𝜆=0⇔11𝜆−11=0⇔𝜆=1. Por tanto, el punto de intersección es 𝑄(2, −1,1). Como 𝑄 es el punto medio de 𝑃 y 𝑃′, podemos hallar 𝑃′ como el simétrico de 𝑃 con respecto de 𝑄. Si llamamos 𝑃′(𝑎,𝑏,𝑐), ha de que verificarse: ⎧{ { { {⎨{ { { {⎩1+𝑎2=2⇔𝑎=3,𝑏2=−1⇔𝑏=−2,−1+𝑐2=1⇔𝑐=3. Por tanto, el punto simétrico de 𝑃 con respecto a la recta 𝑟 es 𝑃′(3, −2,3).
2. Consideramos un punto genérico 𝑅(1 +𝜆, −4 +3𝜆,𝜆) de la recta 𝑟. La distancia entre 𝑃 y el punto genérico 𝑅 viene dada por el módulo del vector ⃗𝑃𝑅 =(𝜆, −4 +3𝜆,𝜆 +1). dist⁡(𝑃,𝑅)=|⃗𝑃𝑅|=√𝜆2+(−4+3𝜆)2+(𝜆+1)2=√𝜆2+16−24𝜆+9𝜆2+𝜆2+2𝜆+1==√11𝜆2−22𝜆+17. Para que la distancia de un punto de 𝑟 a 𝑃 sea de √6 unidades, ha de verificarse: dist⁡(𝑃,𝑅)=√6⇔√11𝜆2−22𝜆+17=√6⇔11𝜆2−22𝜆+17=6⇔11𝜆2−22𝜆+11=0⇔⇔𝜆2−2𝜆+1=0⇔(𝜆−1)2=0⇔𝜆=1. Por tanto, el punto es 𝑄(2, −1,1).